- 2021-06-23 发布 |
- 37.5 KB |
- 6页
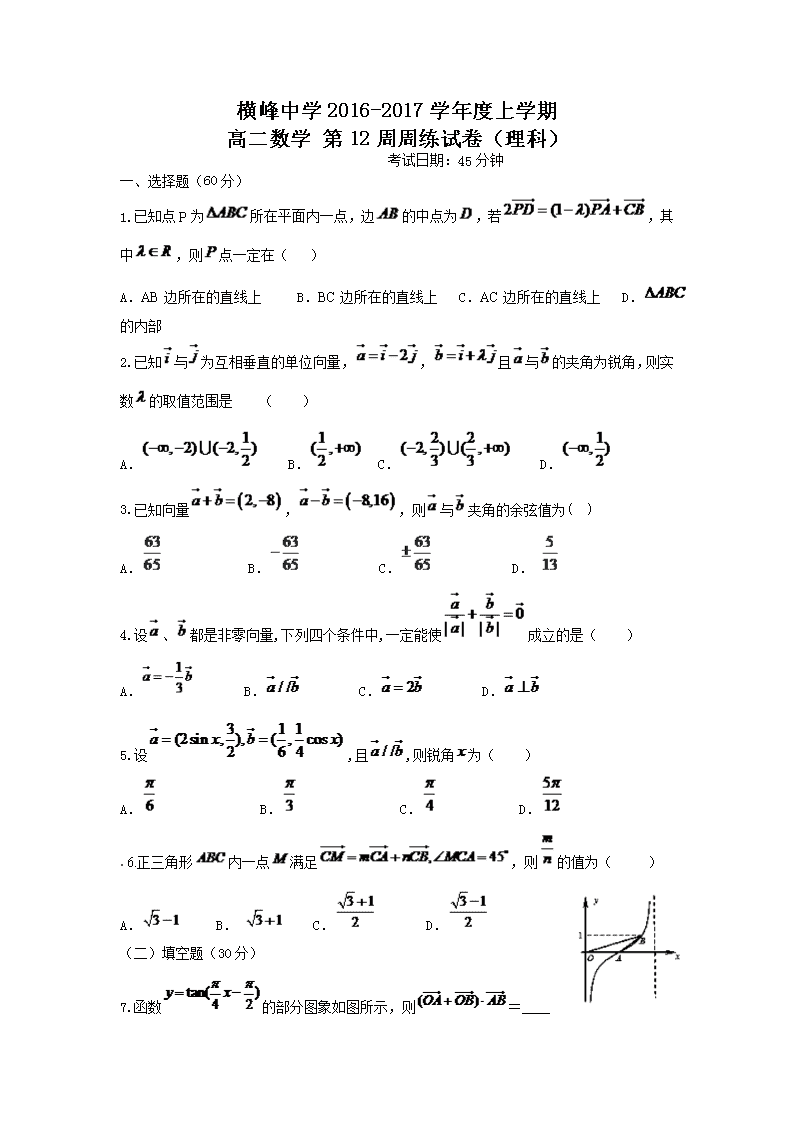

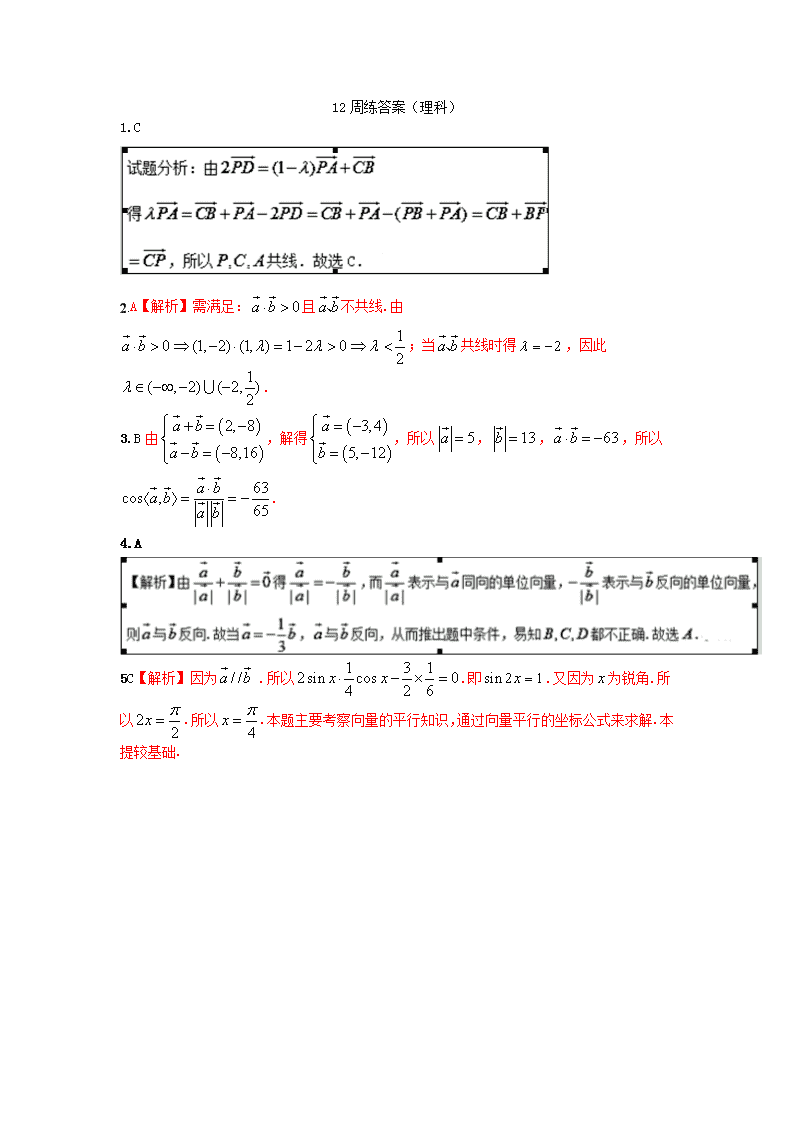
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2017届江西省横峰中学高三上学期第十二周周练(2016
横峰中学2016-2017学年度上学期 高二数学 第12周周练试卷(理科) 考试日期:45分钟 一、选择题(60分) 1.已知点P为所在平面内一点,边的中点为,若,其中,则点一定在( ) A.AB边所在的直线上 B.BC边所在的直线上 C.AC边所在的直线上 D.的内部 2.已知与为互相垂直的单位向量,,且与的夹角为锐角,则实数的取值范围是 ( ) A. B. C. D. 3.已知向量,,则与夹角的余弦值为( ) A. B. C. D. 4.设、都是非零向量,下列四个条件中,一定能使成立的是( ) A. B. C. D. 5.设,且,则锐角为( ) A. B. C. D. .6.正三角形内一点满足,则的值为( ) A. B. C. D. (二)填空题(30分) 7.函数的部分图象如图所示,则=____ 8.若O为△ABC所在平面内任一点,且满足,则△ABC的形状为___ 9.在平面直角坐标系中,是坐标原点,两定点满足,则点集所表示的区域的面积是___________ 【来源:全,品…中&高*考+网】10在△ABC中,内角A,B,C所对的边分别为a,b,c,且a+b+c=8. (1)若a=2,b=,求cos C的值; (2)若sin A+sin B=2sin C,且△ABC的面积S=sin C,求a和b的值. 11.设平面向量,.若存在实数和角, 使向量,,且. (I)求函数的关系式; (II)令,求函数的极值. 12周练答案(理科) 1.C 2.A【解析】需满足:且不共线.由;当共线时得,因此. 3.B由,解得,所以,,,所以. 4.A 5C【解析】因为 .所以.即.又因为为锐角.所以.所以.本题主要考察向量的平行知识,通过向量平行的坐标公式来求解.本提较基础. 6D 7.【答案】B 8..C【解析】因为, 即, 所以是等腰三角形,选C. 9.. 10. 11. 解:(I)由,,得 =,即,得 . (II)由,得 求导得,令,得, 当,,为增函数;当时,,为减函数; 当时,,为增函数. 所以当,即时,有极大值;当,即时,有极小 值.查看更多