2020届二轮复习.向量的减法课件（13张）（全国通用）

2020届二轮复习.向量的减法课件（13张）（全国通用）

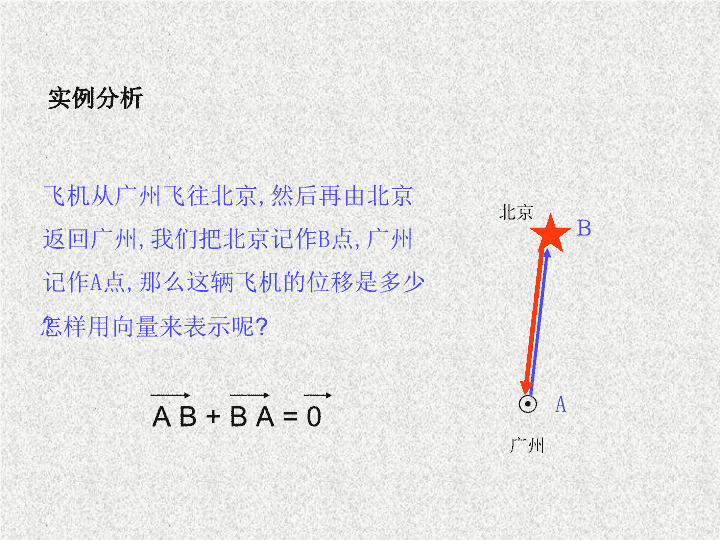
2.2 向量的减法 北京 广州 实例分析 飞机从广州飞往北京 , 然后再由北京返回广州 , 我们把北京记作 B 点 , 广州记作 A 点 , 那么这辆飞机的位移是多少 ? A B + B A = 0 A Ｂ 怎样用向量来表示呢 ? 我们把与 a 长度相等，方向相反的向量，叫作 a 的 相反向量 . 记作 － a ， a 和 － a 互为相反向量 ． 零向量的相反向量仍是零向量． 1 、若 a , b 是互为相反向量 , 那么 a = ____ , b =____, a + b =____ – b – a 0 、 – （ – a ) = 　　 . 　　　 　 a + b 的相反向量是 . a + （ – b ） 的相反向量是 . – ( a + b ) –[ a+ （ – b ） ] a 定义 : 求两个向量差的运算 , 叫做向量的减法 . A C B 小结 : 作两向量的差向量的步骤 : (1) 将两向量移到共同起点 (2) 连接两向量的终点 , 方向指向被减向量 注意与作和向量的区别 例 1 　已知向量 a,b,c, 求作向量 a-b+c. a b c Ｏ Ｂ Ａ C D 例 2 　已知 |a| =6 ,|b| =8, 且 |a+b|=| a- b|, 求 |a- b|. A D B a b C 练习 : 如图：平行四边形 ABCD 中 , 用 表示向量 A B C D 变式二 : 在本例中 , 当 a,b 满足 什么条件时 , | a+b | = | a-b | ? 变式三 : 在本例中 , a+b 与 a-b 有可能相等吗 ? 变式一 : 在本例中 , 当 a,b 满足 什么条件时 ,a+b 与 a-b 相互垂直 ? 变式四 : 在本例中 , | a | , | b | , | a+b |,| a-b | 有什么关系 ? 1 化简 解 练习 2 化简 解 练习 练习 : 书 104 页 T2 3. Δ ABC 中 ,BC=a,CA=b, 则 ,AB=( ) A.a+b B.–(a+b) C. a-b D. b-a 4. 已知 |AB|=8,|AC|=5, 则 |BC| 的取值范围是 ____.