- 2021-06-23 发布 |
- 37.5 KB |
- 7页


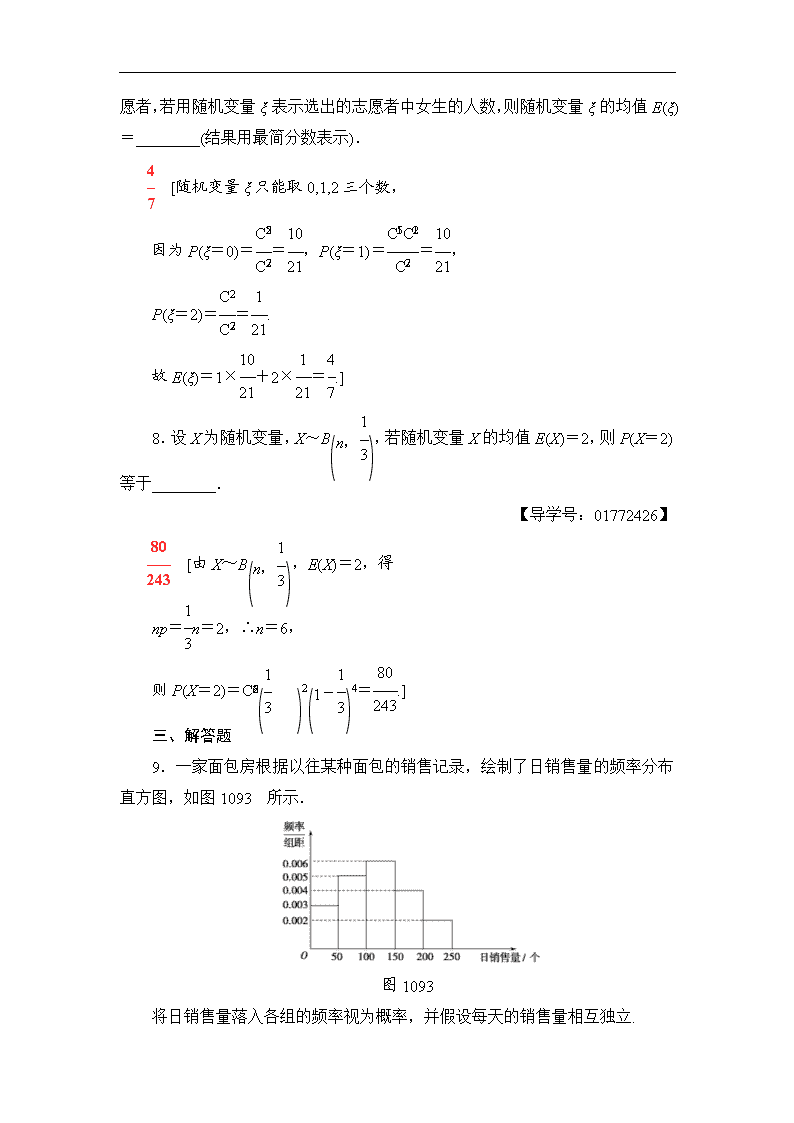
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届高三数学一轮复习: 第10章 第9节 课时分层训练66
课时分层训练(六十六) 离散型随机变量的均值与方差 A组 基础达标 (建议用时:30分钟) 一、选择题 1.已知某一随机变量X的分布列如下,且E(X)=6.3,则a的值为( ) X 4 a 9 P 0.5 0.1 b A.5 B.6 C.7 D.8 C [由分布列性质知:0.5+0.1+b=1,∴b=0.4, ∴E(X)=4×0.5+a·0.1+9×0.4=6.3,∴a=7.] 2.设样本数据x1,x2,…,x10的均值和方差分别为1和4,若yi=xi+a(a为非零常数,i=1,2,…,10),则y1,y2,…,y10的均值和方差分别为( ) A.1+a,4 B.1+a,4+a C.1,4 D.1,4+a A [E(y)=E(x)+a=1+a,D(y)=D(x)=4.] 3.某班有14名学生数学成绩优秀,如果从该班随机找出5名学生,其中数学成绩优秀的学生数X~B,则E(2X+1)=( ) A. B. C.3 D. D [因为X~B,所以E(X)=,则E(2X+1)=2E(X)+1=2×+1=.] 4.已知随机变量X服从二项分布,且E(X)=2.4,D(X )=1.44,则二项分布的参数n,p的值为( ) A.n=4,p=0.6 B.n=6,p=0.4 C.n=8,p=0.3 D.n=24,p=0.1 B [由二项分布X~B(n,p)及E(X)=np,D(X)=np·(1-p)得2.4=np,且1.44=np(1-p), 解得n=6,p=0.4.] 5.罐中有6个红球,4个白球,从中任取1球,记住颜色后再放回,连续摸取4次,设X为取得红球的次数,则X的方差D(X)的值为( ) A. B. C. D. B [因为是有放回地摸球,所以每次摸球(试验)摸得红球(成功)的概率均为,连续摸4次(做4次试验),X为取得红球(成功)的次数,则X~B, ∴D(X)=4××=.] 二、填空题 6.(2015·广东高考)已知随机变量X服从二项分布B(n,p).若E(X)=30,D(X)=20,则p=________. [由E(X)=30,D(X)=20, 可得解得p=.] 7.(2017·唐山调研)某学校要从5名男生和2名女生中选出2人作为社区志愿者,若用随机变量ξ表示选出的志愿者中女生的人数,则随机变量ξ的均值E(ξ)=________(结果用最简分数表示). [随机变量ξ只能取0,1,2三个数, 因为P(ξ=0)==,P(ξ=1)==, P(ξ=2)==. 故E(ξ)=1×+2×=.] 8.设X为随机变量,X~B,若随机变量X的均值E(X)=2,则P(X=2)等于________. 【导学号:01772426】 [由X~B,E(X)=2,得 np=n=2,∴n=6, 则P(X=2)=C24=.] 三、解答题 9.一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图1093所示. 图1093 将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立. 【导学号:01772427】 (1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率; (2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列、均值E(X)及方差D(X). [解] (1)设A1表示事件“日销售量不低于100个”,A2表示事件“日销售量低于50个”,B表示事件“在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个”,因此 P(A1)=(0.006+0.004+0.002)×50=0.6, P(A2)=0.003×50=0.15, P(B)=0.6×0.6×0.15×2=0.108.5分 (2)X可能取的值为0,1,2,3,相应的概率为 P(X=0)=C·(1-0.6)3=0.064, P(X=1)=C·0.6(1-0.6)2=0.288, P(X=2)=C·0.62(1-0.6)=0.432, P(X=3)=C·0.63=0.216.8分 因此随机变量X的分布列为 X 0 1 2 3 P 0.064 0.288 0.432 0.216 因为X~B(3,0.6),所以均值E(X)=3×0.6=1.8, 方差D(X)=3×0.6×(1-0.6)=0.72.12分 10.(2017·广东深圳质检)某校高二年级开设a,b,c,d,e五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选a课程,不选b课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程. (1)求甲同学选中c课程且乙同学未选中c课程的概率; (2)用X表示甲、乙、丙选中c课程的人数之和,求X的分布列和数学期望. 【导学号:01772428】 [解] (1)设“甲同学选中c课程”为事件A,“乙同学选中c课程”为事件B,依题意P(A)==,P(B)==.2分 (1)因为事件A与B相互独立,所以甲同学选中c课程且乙同学未选中c课程的概率为 P(A)=P(A)P()=P(A)[1-P(B)]=×=.4分 (2)设事件C为“丙同学选中c课程”. 则P(C)==.5分 X的可能取值为0,1,2,3. P(X=0)=P()=××=, P(X=1)=P(A)+P(B)+P(C) =××+××+××==, P(X=2)=P(AB)+P(AC)+P(BC) =××+××+××==, P(X=3)=P(ABC)=××==,8分 随机变量X的分布列为 X 0 1 2 3 P 所以E(X)=0×+1×+2×+3×=.12分 B组 能力提升 (建议用时:15分钟) 1.从装有除颜色外完全相同的3个白球和m个黑球的布袋中随机摸取一球,有放回地摸取5次,设摸得白球数为X,已知E(X)=3,则D(X)=( ) A. B. C. D. B [由题意,X~B. 又E(X)==3,∴m=2. 则X~B,故D(X)=5××=.] 2.随机变量ξ的取值为0,1,2.若P(ξ=0)=,E(ξ)=1,则D(ξ)=________. 【导学号:01772429】 [设P(ξ=1)=a,P(ξ=2)=b, 则解得 所以D(ξ)=+×0+×1=.] 3.(2017·泉州模拟)某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为,中奖可以获得2分;方案乙的中奖率为,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品. (1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率; (2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大? [解] (1)由已知得,小明中奖的概率为,小红中奖的概率为,且两人中奖与否互不影响. 记“这2人的累计得分X≤3”为事件A, 则事件A的对立事件为“X=5”.2分 因为P(X=5)=×=, 所以P(A)=1-P(X=5)=, 即这2人的累计得分X≤3的概率为.5分 (2)法一:设小明、小红都选择方案甲抽奖中奖次数为X1,得分为Y1,都选择方案乙抽奖中奖次数为X2,累计得分为Y2,则Y1=2X1,Y2=3X2. 由已知可得,X1~B,X2~B,6分 所以E(X1)=2×=, E(X2)=2×=, 因此E(Y1)=2E(X1)=, E(Y2)=3E(X2)=.8分 因为E(2X1)>E(3X2),即E(Y1)>E(Y2), 所以他们都选择方案甲进行抽奖时,累计得分的均值较大.12分 法二:依题意,累计得分Y1,Y2的分布列为: Y1 0 2 4 P Y2 0 3 6 P 所以E(Y1)=0×+2×+4×=, E(Y2)=0×+3×+6×=.8分 因为E(Y1)>E(Y2), 所以二人都选择方案甲抽奖,累计得分的均值较大.12分查看更多