江苏省南通市2020届高三第二次模拟考试（5月） 数学

江苏省南通市2020届高三第二次模拟考试（5月） 数学

‎2020届高三模拟考试试卷 数　　学 ‎(满分160分，考试时间120分钟)‎ ‎2020．5‎ 参考公式：‎ 样本数据x1，x2，…，xn的方差s2＝圆柱的体积公式：V圆柱＝Sh，其中S是圆柱的底面积，h为高．‎ 圆柱的侧面积公式：S圆柱侧＝cl，其中c是圆柱底面的周长，l为母线长．‎ 球的体积公式：V球＝πR3，球的表面积公式：S球＝4πR2，其中R为球的半径．‎ 一、 填空题：本大题共14小题，每小题5分，共70分．‎ ‎1. 已知集合M＝{－2，－1，0，1}，N＝{x|x2＋x≤0}，则M∩N＝________．‎ ‎2. 已知复数为纯虚数，其中i为虚数单位，则实数a的值是________．‎ ‎3. 某同学5次数学练习的得分依次为114，116，114，114，117，则这5次得分的方差是________．‎ Read x If x＜0 Then ‎　 m←2x＋1‎ Else ‎　 m←2－3x End If Print m ‎　 (第4题)‎ ‎4. 根据如图所示的伪代码，当输入的x为－1时，最后输出m的值是________．‎ ‎5. 在平面直角坐标系xOy中，若双曲线－＝1(a>0，b>0)的离心率为，则该双曲线的渐近线的方程是____________．‎ ‎6. 某同学参加“新冠肺炎防疫知识”答题竞赛活动，需从4道题中随机抽取2道作答．若该同学会其中的3道题，则抽到的2道题他都会的概率是________．‎ ‎7. 将函数f(x)＝sin(2x＋)的图象向右平移φ个单位长度得到函数g(x)的图象．若g(x)为奇函数，则φ的最小正值是________．‎ ‎8. 已知非零向量b与a的夹角为120°，且|a|＝2，|2a＋b|＝4，则|b|＝________．‎ ‎9. 已知等比数列{an}的各项均为正数，且8a1，a3，6a2成等差数列，则的值是________．‎ ‎10. 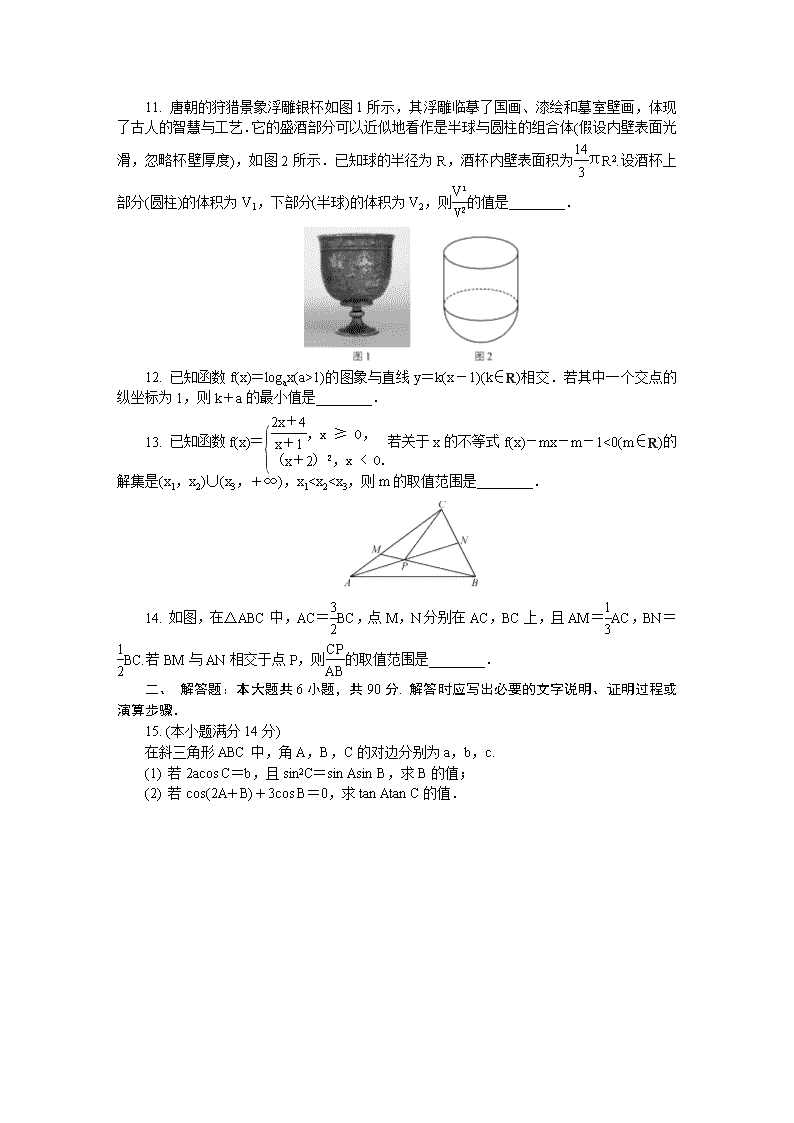在平面直角坐标系xOy中，已知过点(－10，0)的圆M与圆x2＋y2－6x－6y＝0相切于原点，则圆M的半径是________．‎ ‎11. 唐朝的狩猎景象浮雕银杯如图1所示，其浮雕临摹了国画、漆绘和墓室壁画，体现了古人的智慧与工艺．它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑，忽略杯壁厚度)，如图2所示．已知球的半径为R，酒杯内壁表面积为πR2.设酒杯上部分(圆柱)的体积为V1，下部分(半球)的体积为V2，则的值是________．‎ ‎12. 已知函数f(x)＝logax(a>1)的图象与直线y＝k(x－1)(k∈R)相交．若其中一个交点的纵坐标为1，则k＋a的最小值是________．‎ ‎13. 已知函数f(x)＝若关于x的不等式f(x)－mx－m－1<0(m∈R)的解集是(x1，x2)∪(x3，＋∞)，x10，b>0)短轴的两个顶点与右焦点的连线构成等边三角形，两准线之间的距离为.‎ ‎(1) 求椭圆C的标准方程；‎ ‎(2) 直线l：y＝kx＋m(k>0，m≠0)与椭圆C交于P，Q两点，设直线OP，OQ的斜率分别为k1，k2.已知k2＝k1·k2.‎ ‎①求k的值；‎ ‎②当△OPQ的面积最大时，求直线PQ的方程．‎ ‎19. (本小题满分16分)‎ 已知数列{an}的前n项和为Sn，a1＝1，λan＋1＋Sn·Sn＋2＝S，n∈N*，λ∈R.‎ ‎(1) 若λ＝－3，a2＝－1，求a3的值；‎ ‎(2) 若数列{an}的前k项成公差不为0的等差数列，求k的最大值；‎ ‎(3) 若a2>0，是否存在λ∈R，使{an}为等比数列？若存在，求出所有符合题意的λ的值；若不存在，请说明理由．‎ ‎20. (本小题满分16分)‎ 对于定义在D上的函数f(x)，若存在k∈R，使f(x)0)，过点M(4p，0)的直线l交抛物线于A(x1，y1)，B(x2，y2)两点．当AB垂直于x轴时，△OAB的面积为2.‎ ‎(1) 求抛物线的方程；‎ ‎(2) 设线段AB的垂直平分线交x轴于点T.‎ ‎①求证：y1y2为定值；‎ ‎②若OA∥TB，求直线l的斜率．‎ ‎23. 设n∈N*，k∈N，n≥k.‎ ‎(1) 化简：；‎ ‎(2) 已知(1－x)2n＝a0＋a1x＋a2x2＋…＋a2nx2n，记F(n)＝(n＋1).求证：F(n)能被2n＋1整除．‎ ‎2020届高三模拟考试试卷(南通)‎ 数学参考答案及评分标准 ‎1. {－1，0}　2. －　3. 　4. 　5. y＝±2x　6. 　7. 　8. 4　9. 16　10. 5　11. 2　12. 3　13. (0，2)∪(2，3)　14. (，2)‎ ‎15. 解： (1) 在△ABC中，由余弦定理得2a·＝b，‎ 化简得a2＝c2，即a＝c.(2分)‎ 因为sin2C＝sin Asin B，且＝＝＝2R(R为△ABC外接圆半径)，‎ 所以c2＝ab，(4分)‎ 所以c＝a＝b，所以△ABC为正三角形，‎ 所以B＝.(6分)‎ ‎(2) 因为cos(2A＋B)＋3cos B＝0，且B＝π－(A＋C)，‎ 所以cos[π＋(A－C)]＋3cos[π－(A＋C)]＝0，(8分)‎ 所以cos(A－C)＝－3cos(A＋C)，(10分)‎ 即cos Acos C＋sin Asin C＝－3cos Acos C＋3sin Asin C，‎ 所以2cos Acos C＝sin Asin C．(12分)‎ 在斜三角形ABC中，因为A≠，C≠，所以cos A≠0，cos C≠0，‎ 所以tan Atan C＝2.(14分)‎ ‎16. 证明：(1) 因为侧面BCC1B1是矩形，所以BC⊥CC1.‎ 因为平面ACC1A1⊥平面BCC1B1，平面ACC1A1∩平面BCC1B1＝C1C，BC⊂平面BCC1B1，‎ 所以BC⊥平面ACC1A1.(4分)‎ 因为AC1⊂平面ACC1A1，‎ 所以BC⊥AC1.(6分)‎ ‎(2) 取A1C1的中点G，连结FG，CG.‎ 在△A1B1C1中，点F，G分别是A1B1，A1C1的中点，‎ 所以FG∥B1C1，且FG＝B1C1.(8分)‎ 在矩形BCC1B1中，点E是BC的中点，‎ 所以EC∥B1C1，且EC＝B1C1，‎ 所以EC∥FG，且EC＝FG.(10分)‎ 所以四边形EFGC为平行四边形，‎ 所以EF∥GC.(12分)‎ 因为EF⊄平面ACC1A1，GC⊂平面ACC1A1，‎ 所以EF∥平面ACC1A1.(14分)‎ ‎17. 解：方案1：因为AB⊥AC，‎ 所以∠EAC＋∠BAD＝90°.‎ 在Rt△ABD中，∠ABD＋∠BAD＝90°，‎ 所以∠EAC＝∠ABD＝α，α∈(0，)．(2分)‎ 因为AD＝AE＝50，‎ 在Rt△ADB和Rt△AEC中，AB＝，AC＝，(4分)‎ 所以BC＝＝50＝，‎ 所以f(α)＝50(＋＋)＝50()，其中α∈(0，)．(7分)‎ ‎(解法1)设t＝sin α＋cos α，则t＝sin α＋cos α＝sin(α＋)．‎ 因为α∈(0，)，所以t∈(1，]．(9分)‎ 因为t2＝1＋2sin αcos α，所以sin αcos α＝，‎ 所以y＝＝，(12分)‎ 所以当t＝时，f(α)min＝＝100＋100.‎ 答：景观桥总长度的最小值为(100＋100)米．(14分)‎ ‎(解法2)f′(α)＝.(10分)‎ 因为α∈(0，)，所以－1－sin αcos α－sin α－cos α<0，(sin αcos α)2>0.‎ 当α∈(0，)时，cos α－sin α>0，f′(α)<0，f(α)单调递减；‎ 当α∈(，)时，cos α－sin α<0，f′(α)>0，f(α)单调递增．(12分)‎ 所以当α＝时，f(α)取得最小值，最小值为(100＋100)米．‎ 答：景观桥总长度的最小值为(100＋100)米．(14分)‎ 方案2：因为AB⊥AC，所以∠EAC＋∠BAD＝90°.‎ 在Rt△ABD中，∠ABD＋∠BAD＝90°，‎ 所以∠EAC＝∠ABD，‎ 所以Rt△CAE∽Rt△ABD, ‎ 所以＝.(2分)‎ 因为EC＝x，AC＝＝，AD＝50，‎ 所以AB＝.(4分)‎ BC＝＝＝x＋，‎ 所以g(x)＝＋＋(x＋)，x>0.(7分)‎ 因为x>0，‎ 所以g(x)≥2＋2(10分)‎ ‎＝2＋100≥2＋100＝100＋100.(12分)‎ 当且仅当＝，且＝x，即x＝50时取“＝”．‎ 所以g(x)min＝100＋100，‎ 答：景观桥总长度的最小值为(100＋100)米．(14分)‎ ‎18. 解：(1) 设椭圆的焦距为2c，则c2＝a2－b2.‎ 因为短轴的两个顶点与右焦点的连线构成等边三角形，所以c＝b.‎ 又两准线间的距离为，则＝，所以a＝2，b＝1，‎ 所以椭圆C的标准方程为＋y2＝1.(3分)‎ ‎(2) ① 设P(x1，y1)，Q(x2，y2)，‎ 联立消去y得(4k2＋1)x2＋8kmx＋4m2－4＝0，‎ Δ＝64k2m2－4(4k2＋1)(4m2－4)>0，化简得m2<4k2＋1，‎ 所以x1＋x2＝，x1x2＝.‎ 又OP的斜率k1＝，OQ的斜率k2＝，‎ 所以k2＝k1·k2＝＝＝，(6分)‎ 化简得km(x1＋x2)＋m2＝0，‎ 所以km·＋m2＝0.‎ 因为m≠0，即4k2＝1，又k>0，所以k＝.(8分)‎ ‎②由①得k＝，直线PQ的方程为y＝x＋m，‎ 且x1＋x2＝－2m，x1x2＝2m2－2，m2<2.‎ 又m≠0，所以0<<.‎ 所以PQ＝＝|x1－x2|＝＝·，(10分)‎ 点O到直线PQ的距离d＝＝|m|，(12分)‎ 所以S△OPQ＝PQ·d＝×··|m|＝≤＝1，‎ 当且仅当m2＝2－m2，即m＝±1时，△OPQ的面积最大，‎ 所以直线PQ的方程为y＝x±1.(16分)‎ ‎19. 解：记λan＋1＋Sn·Sn＋2＝S为(*)式．‎ ‎(1) 当λ＝－3时，(*)式为－3an＋1＋Sn·Sn＋2＝S，‎ 令n＝1得－3a2＋S1·S3＝S，即－3a2＋a1·(a1＋a2＋a3)＝(a1＋a2)2.‎ 由已知a1＝1，a2＝－1，解得a3＝－3.(2分)‎ ‎(2) 因为前k项成等差数列，设公差为d，则a2＝1＋d，a3＝1＋2d.‎ 若k＝3，则S2＝2＋d，S3＝3＋3d.‎ 在(*)式中，令n＝1得λa2＋S1·S3＝S，所以λ(1＋d)＋3＋3d＝(2＋d)2，‎ 化简得d2＋d＋1＝λ(1＋d)　①.(4分)‎ 若k＝4，则S4＝4＋6d.‎ 在(*)式中，令n＝2得λa3＋S2·S4＝S，所以λ(1＋2d)＋(2＋d)(4＋6d)＝(3＋3d)2，‎ 化简得3d2＋2d＋1＝λ(1＋2d)　②.‎ ‎②－①，得2d2＋d＝λd，因为公差不为0，所以d≠0，‎ 所以2d＋1＝λ，代入①得d2＋2d＝0，所以d＝－2，λ＝－3.‎ 所以k＝4符合题意．(6分)‎ 若k＝5，则a1＝1，a2＝－1，a3＝－3，a4＝－5，a5＝－7，S3＝－3，S4＝－8，S5＝－15.‎ 在(*)式中，令n＝3得－3a4＋S3S5＝－3×(－5)＋(－3)×(－15)＝60，S＝(－8)2＝64，‎ 所以－3a4＋S3S5≠S，所以k的最大值为4.(8分)‎ ‎(3) 假设存在λ∈R，使{an}为等比数列．‎ 设前3项分别为1，q，q2，则S1＝1，S2＝1＋q，S3＝1＋q＋q2，‎ ‎(*)式中，令n＝1得λq＋(1＋q＋q2)＝(1＋q)2，化简得q(λ－1)＝0.‎ 因为q＝a2>0，所以λ＝1.(10分)‎ 此时(*)式为(Sn＋1－Sn)＋Sn·Sn＋2＝S，即Sn＋1(Sn＋1－1)＝Sn(Sn＋2－1)　(**)．‎ 由S1＝1，S2＝1＋a2>1，得S3>1; 由S2，S3>1得S4>1，…‎ 依次类推，Sn≥1>0，所以(**)等价于＝，‎ 所以数列为常数列，‎ 所以＝＝a2.(14分)‎ 于是n≥2时，两式相减得an＋1＝a2·an.‎ 因为a2＝a2·a1，所以an＋1＝a2·an(n∈N*)．‎ 又a1，a2≠0，所以＝a2(非零常数)，所以存在λ＝1，使{an}为等比数列．(16分)‎ ‎20. (1)解：a＝0时，h1(x)＝ln x＋1.‎ 因为h1(x)为“m(k)型函数”，所以h1(x)恒成立．‎ 设g(x)＝(x≥1)，则g′(x)＝≤0恒成立，‎ 所以g(x)在[1，＋∞)上单调递减，所以g(x)≤g(1)＝1，‎ 所以k的取值范围是(1，＋∞)．(3分)‎ ‎(2) 证明：当a＝－时，要证h2(x)为“M(1)型函数”，‎ 即证(1＋x)ln x＋≥x，即证(1＋x)ln x＋－x≥0.‎ ‎(证法1)令R(x)＝(1＋x)ln x＋－x，‎ 则R′(x)＝ln x＋(1＋x)·－－1＝ln x＋－＝ln x＋.‎ 当x>1时，ln x>0，>0，则R′(x)>0；‎ 当00，‎ 所以函数F(x)在(0，＋∞)上单调递增，又F(1)＝0，‎ 所以当01时，R′(x)>0，‎ 所以R(x)在(0，1)上单调递减，在(1，＋∞)上单调递增，(6分)‎ 以下同证法1.‎ ‎(3) 证明：函数f(x)为“m()型函数”等价于p(x)＝(1－2ax)ln x－x<0恒成立，‎ 当a≤0时，p(e)＝(1－2ae)－≥1－>0，不合题意；‎ 当a≥2时，p()＝－1－≥(4－e－)>0，不合题意；(10分)‎ 当a＝1时，‎ ‎(证法1)p(x)＝(1－2x)ln x－x，‎ ‎①当x≥1或0，‎ 所以p(x)<－x＝(3x－2)2≤0.‎ 综上，存在唯一整数a＝1，使得f(x)为“m()型函数”．(16分)‎ ‎(证法2)p(x)＝(1－2x)ln x－x，p′(x)＝－2ln x＋－＝－2ln x＋－.‎ 记φ(x)＝－2ln x＋－，则φ′(x)＝－<0，‎ 所以φ(x)＝p′(x)在(0，＋∞)上单调递减．‎ 易得ln x≤x－1，‎ 所以p′()＝2ln ＋－≤2(－1)＋－＝3－＝<0.‎ 因为p′()＝2ln 2＋2－>1＋2－>0，‎ 所以存在唯一零点x0∈(，)，使得p′(x0)＝－2ln x0＋－＝0，‎ 且x0为p(x)的最大值点，(12分)‎ 所以p(x0)＝(1－2x0)ln x0－x0＝－x0＝2x0＋－.‎ 注意到y＝2x＋－在(，)上单调递增，‎ 所以p(x0)0，所以p＝，‎ 所以抛物线的方程为y2＝x.(3分)‎ ‎(2) ①证明：由题意可知直线l与x轴不垂直．‎ 由(1)知M(2，0)，设A(y，y1)，B(y，y2)，则kAB＝＝.‎ 由A，M，B三点共线，得＝.‎ 因为y1≠y2，化简得y1y2＝－2.(5分)‎ ‎②解：因为y1y2＝－2，所以B(，－)．‎ 因为线段AB垂直平分线的方程为y－＝－(y1＋y2)(x－)，‎ 令y＝0，得xT＝＝(y＋＋1)．(7分)‎ 因为OA∥TB，所以kOA＝kTB，即＝，‎ 整理得(y＋1)(y－4)＝0，解得y1＝±2，故A(4，±2)．‎ 所以kAM＝±1，即直线l的斜率为±1.(10分)‎ ‎23. (1) 解：＝ ‎＝＝.(3分)‎ ‎(2) 证明：由(1)得＝·＝· ‎＝·(＋)．(6分)‎ 因为＝＝·，‎ 所以F(n)＝(n＋1)＝·.‎ 因为 ‎＝(＋＋…＋＋)＋(＋＋…＋＋)‎ ‎＝＋(＋)＋…＋(＋)＋ ‎＝(＋＋…＋＋)＋＝2n，‎ 所以F(n)＝(n＋1)＝·2n＝n(2n＋1)能被2n＋1整除．(10分)‎