专题41 利用样本的数字特征估计总体-备战2017年高考高三数学一轮热点难点一网打尽

专题41 利用样本的数字特征估计总体-备战2017年高考高三数学一轮热点难点一网打尽

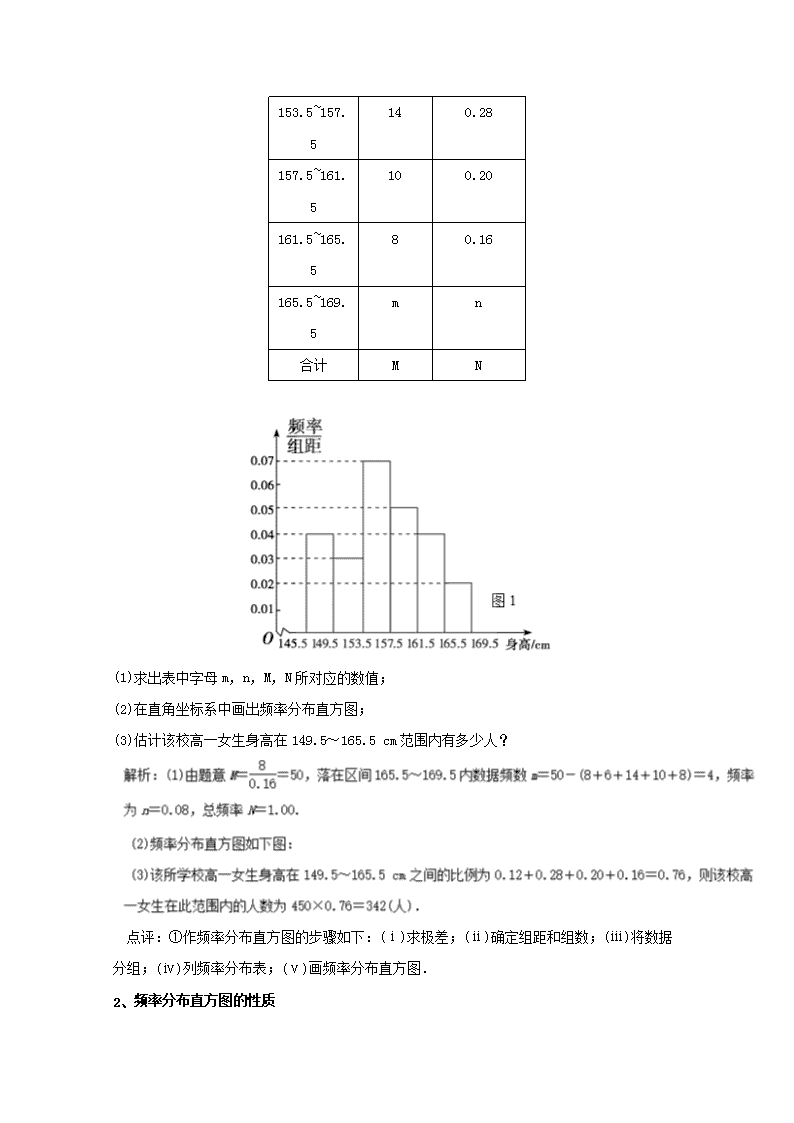
www.ks5u.com ‎【备战2017年高考高三数学一轮热点、难点一网打尽】‎ 第41讲 利用样本的数字特征估计总体 考纲要求:‎ ‎1．了解分布的意义与作用，能根据频率分布表画频率分布直方图、频率折线图、茎叶图，体会它们各自的特点．　‎ ‎2．理解样本数据标准差的意义和作用，会计算数据标准差．　‎ ‎3.能从样本数据中提取基本的数字特征(如平均数、标准差)，并做出合理的解释．　‎ ‎4.会用样本的频率分布估计总体分布，会用样本的基本数字特征估计总体的基本数字特征，理解用样本估计总体的思想．　‎ ‎5.会用随机抽样的基本方法和样本估计总体的思想解决一些简单的实际问题．‎ 基础知识回顾:‎ ‎1、样本的抽取：常用的三种抽样方法：简单随机抽样、系统抽样、分层抽样．‎ ‎2、用样本估计总体：‎ ‎（1）在研究总体时，常用样本的频率分布去估计总体分布：‎ ‎ ①作频率分布直方图的步骤如下：(ⅰ)求极差；(ⅱ)确定组距和组数；(ⅲ)将数据分组；(ⅳ)列频率分布表；(ⅴ)画频率分布直方图．频率分布直方图能很容易地表示大量数据，非常直观地表明分布的形状．‎ ‎ ②频率分布直方图的性质：在频率分布直方图中，小长方形的面积＝组距×＝频率．各小长方形的面积之和等于1.小长方形的高＝，所有小长方形的高的和为．‎ ‎ ③频率分布折线图和总体密度曲线：连接频率分布直方图中各小长方形上端的中点，就得到频率分布折线图．随着样本容量的增加，作图时所分的组数增加，组距减小，相应的频率分布折线图就会越来越接近于一条光滑的曲线，统计中称之为总体密度曲线．‎ ‎（2）茎叶图：当样本数据较少时，用茎叶图表示数据的效果较好，它不但可以保留原始信息，而且可以随时记录，给记录和表示都带来方便．‎ ‎（3）用样本的数字特征估计总体的数字特征： 样本的 标准差、方差描述了一组数据围绕平均数波动的大小．标准差、方差越大，数据的离散程度越大，标准差、方差越小，数据的离散程度越小，因为方差与原始数据的单位不同，且平方后可能夸大了偏差的程度，所以虽然方差与标准差在刻画样本数据的分散程度上是一样的，但在解决实际问题时，一般多采用标准差．通常用样本方差估计总体方差，当样本容量接近总体容量时，样本方差很接近总体方差．注：样本的数字特征如表一所示：‎ 表一 答案：最多，最中间，中位数，， ‎ 应用举例:‎ 类型一：频率分布直方图 1、 绘制频率分布直方图 例1、某中学高一女生共有450人，为了了解高一女生的身高情况，随机抽取部分高一女生测量身高，所得数据整理后列出频率分布表如下：‎ 组别 频数 频率 ‎145.5~149.5‎ ‎8‎ ‎0.16‎ ‎149.5~153.5‎ ‎6‎ ‎0.12‎ ‎14‎ ‎0.28‎ ‎153.5~157.5‎ ‎157.5~161.5‎ ‎10‎ ‎0.20‎ ‎161.5~165.5‎ ‎8‎ ‎0.16‎ ‎165.5~169.5‎ m n 合计 M N ‎(1)求出表中字母m，n，M，N所对应的数值；‎ ‎(2)在直角坐标系中画出频率分布直方图；‎ ‎(3)估计该校高一女生身高在149.5～165.5 cm范围内有多少人？‎ ‎　点评：①作频率分布直方图的步骤如下：(ⅰ)求极差；(ⅱ)确定组距和组数；(ⅲ)将数据分组；(ⅳ)列频率分布表；(ⅴ)画频率分布直方图．‎ 1、 频率分布直方图的性质 例2、‎ 某中学为了解学生的数学学习情况，在3000名学生中随机抽取200名，并统计这200名学生的某次数学考试成绩，得到了样本的频率分布直方图，根据频率分布直方图，推测这3000名学生在该次数学考试中成绩小于60分的学生数是 ．‎ 解析：根据频率分布直方图，得在该次数学考试中成绩小于分的频率是 ‎，所以在该次数学考试中成绩小于分的学生人数为 人．‎ 例3、某校从参加高一年级期中考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六段后得到如图所示的部分频率分布直方图.观察图形的信息，则＝，‎ ‎ s＝＝＞s，故甲更稳定，故选甲．‎ 点评：‎ ‎1．用样本估计总体时，样本的平均数、标准差只是总体的平均数、标准差的近似．实际应用中，需先计算数据的平均数，分析平均水平，再计算方差(标准差)分析稳定情况．‎ ‎2．若给出图形，一方面可以由图形得到相应的样本数据，再计算平均数、方差(标准差)；另一方面，可以从图形直观分析样本数据的分布情况，大致判断平均数的范围，并利用数据的波动性大小比较方差(标准差)的大小．‎ 方法、规律归纳:‎ ‎1、利用频率分布直方图求众数、中位数与平均数时，易出错，应注意区分这三者．在频率分布直方图中：‎ ‎(1)最高的小长方形底边中点的横坐标即是众数；‎ ‎(2)中位数左边和右边的小长方形的面积和是相等的；‎ ‎(3)平均数是频率分布直方图的“重心”，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和．‎ ‎2．易把直方图与条形图混淆：两者的区别在于条形图是离散随机变量，纵坐标刻度为频数或频率，直方图是连续随机变量，连续随机变量在某一点上是没有频率的．‎ ‎3．易忽视频率分布直方图中纵轴表示的应为.‎ ‎4．在绘制茎叶图时，易遗漏重复出现的数据，重复出现的数据要重复记录，同时不要混淆茎叶图中茎与叶的含义．‎ 实战演练:‎ ‎1、如图是一名篮球运动员在五场比赛中所得分数的茎叶图，则该运动员在这五场比赛中得分的平均数、中位数分别为（ ）‎ A. 14，12 B. 12，14 C. 14，10 D. 10，12‎ ‎2．在某中学举行的环保知识竞赛中，将三个年级参赛的学生的成绩进行整理后分为5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组，已知第二小组的频数是40，则成绩在80-100分的学生人数是（ ）‎ A. 15 B. 18 C. 20 D. 25‎ 解析∶第二组的频率是，所有参赛的学生人数为 ，那么80-100分的频率是 ，所以人数为 ，选故A.‎ ‎3．对一批产品的长度(单位：毫米)进行抽样检测，下图为检测结果的频率分布直方图．根据标准，产品长度在区间上为三等品．用频率估计概率，现从该批产品中随机抽取1件，则其为二等品的概率是(　　)‎ A．0.09 B．0.20 C．0.25 D．0.45‎ ‎4．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，下图是据北京某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位：毫克/立方米)列出的茎叶图，则甲、乙两地浓度的中位数较低的是(　　)‎ A.甲、乙相等 B．甲 C．乙 D．无法确定 解析：由茎叶图可得甲地浓度的中位数为0.066，乙地浓度的中位数为0.062，因此乙地浓度的中位数较低．答案：C ‎5．某篮球队甲、乙两名运动员练习投篮，每人练习10组，每组投篮40个．命中个数的茎叶图如下图，则下面结论中错误的一个是( )‎ A．甲的极差是29 ‎ B．乙的众数是21‎ C．甲的命中率比乙高 D．甲的中位数是24‎ 解析：A中极差为37-8=29；B中乙的众数为21；C中甲的平均数大，所以命中率高；D中甲的中位数为23‎ ‎6．某班级有50名学生，其中有30名男生和20名女生．随机询问了该班五名男生和五名女生在某次数学测验中的成绩，五名男生的成绩分别为86,94,88,92,90，五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是(　　)‎ A．这种抽样方法是一种分层抽样 C．这五名男生成绩的方差大于这五名女生成绩的方差 B．这种抽样方法是一种系统抽样 D．该班男生成绩的平均数小于该班女生成绩的平均数 ‎7．下图是2015年某市举办青少年运动会上，7位裁判为某武术队员打出的分数的茎叶图，左边数字表示十位数字，右边数字表示个位数字.‎ 这些数据的中位数是______,去掉一个最低分和最高分后所剩数据的平均数是 A. ; B.; C. ; D. ;‎ 解析：中位数为由小到大排列后位于中间的数，即为88，平均数为 ‎8.一个容量为200的样本的频率分布直方图如图所示，则样本数据落在，得到的频率分布直方图如图所示．下表是年龄的频率分布表.‎ 区间 ‎[25, 30)‎ ‎[30,35)‎ ‎[35,40)‎ ‎[40,45)‎ 人数 ‎25‎ a b ‎ (1)求正整数a，b，N的值；‎ ‎(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人，则年龄在第1,2,3组的人数分别是多少？‎ ‎(3)在(2)的条件下，从这6人中随机抽取2人参加社区宣传交流活动，求恰有1人在第3组的概率．‎ 解：(1)由频率分布直方图可知，[25,30)与[30,35)两组的人数相同，所以a＝25.‎ 且b＝25×＝100.总人数N＝＝250.‎ ‎(2)因为第1,2,3组共有25＋25＋100＝150人，利用分层抽样在150名员工中抽取6人，每组抽取的人数分别为：第1组的人数为6×＝1，第2组的人数为6×＝1，第3组的人数为6×＝4，‎ 所以第1,2,3组分别抽取1人，1人，4人．‎ ‎(3)由(2)可设第1组的1人为A，第2组的1人为B，第3组的4人分别为C1，C2，C3，C4，则从6人中抽取2人的所有可能结果为：‎ ‎(A，B)，(A，C1)，(A，C2)，(A，C3)，(A，C4)，(B，C1)，(B，C2)，(B，C3)，(B，C4)，(C1，C2)，(C1，C3)，(C1，C4)，(C2，C3)，(C2，C4)，(C3，C4)，共有15种．‎ 其中恰有1人年龄在第3组的所有结果为：(A，C1)，(A，C2)，(A，C3)，(A，C4)，(B，C1)，(B，C2)，(B，C3)，(B，C4)，共有8种．所以恰有1人年龄在第3组的概率为.‎