2020届高三数学（理）“大题精练”6

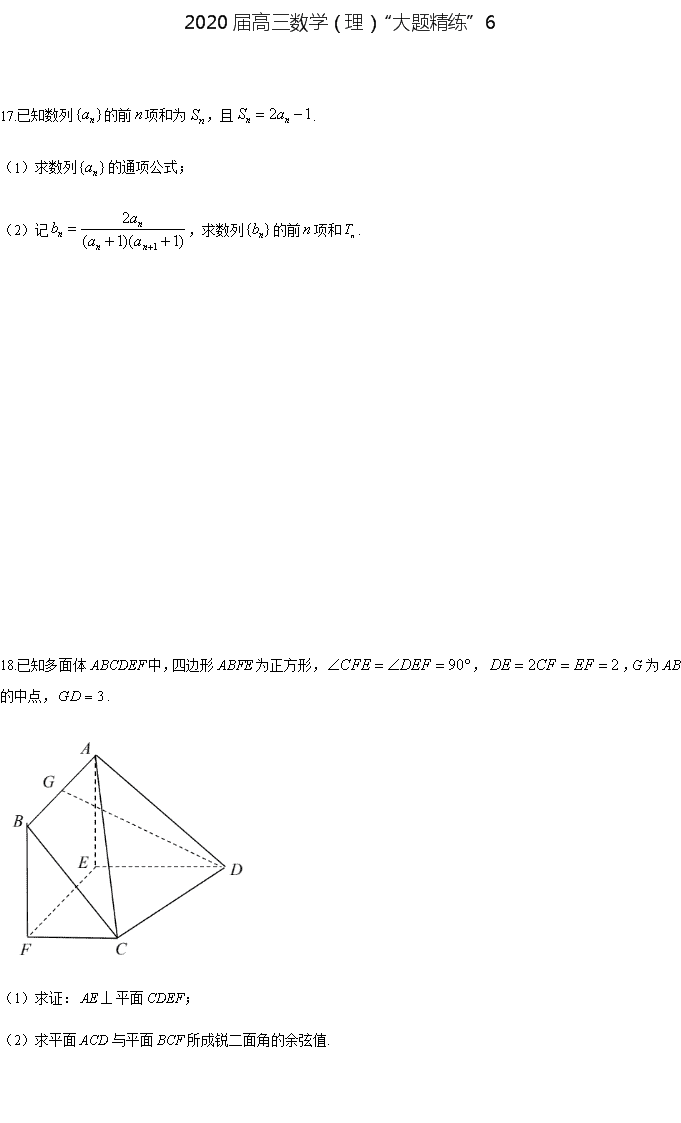
2020届高三数学（理）“大题精练”6

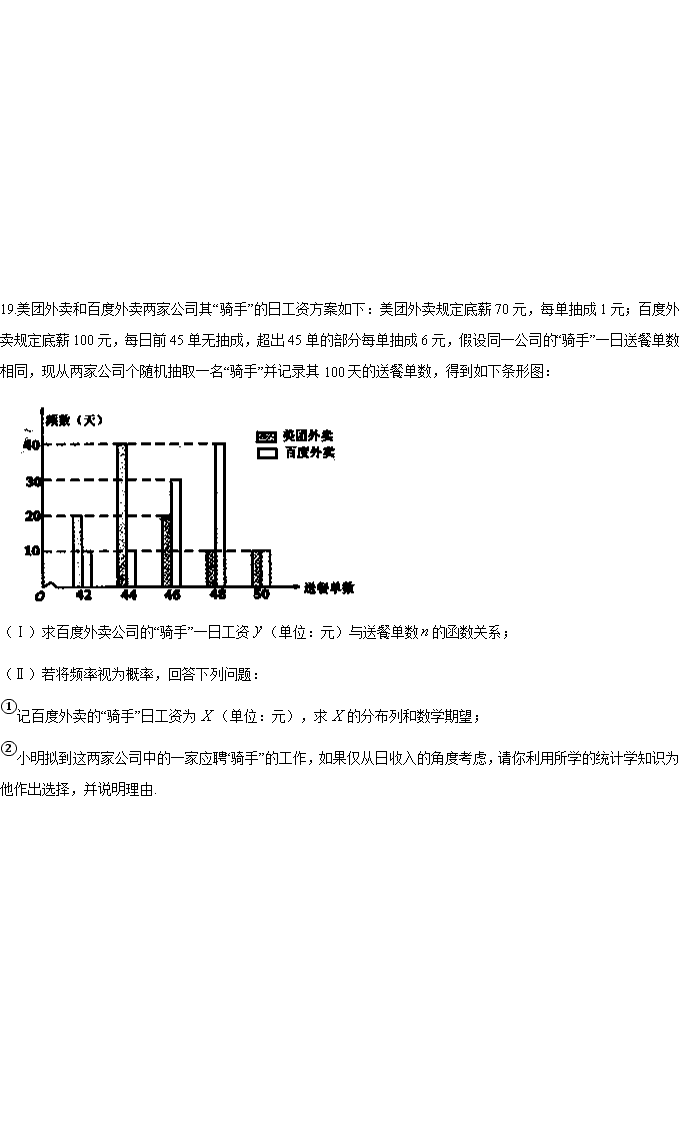
‎2020届高三数学（理）“大题精练”6‎ ‎17.已知数列的前项和为，且.‎ ‎（1）求数列的通项公式；‎ ‎（2）记，求数列的前项和.‎ ‎18.已知多面体ABCDEF中，四边形ABFE为正方形，，，G为AB的中点，.‎ ‎（1）求证：平面CDEF；‎ ‎（2）求平面ACD与平面BCF所成锐二面角的余弦值.‎ ‎19.美团外卖和百度外卖两家公司其“骑手”的日工资方案如下：美团外卖规定底薪70元，每单抽成1元；百度外卖规定底薪100元，每日前45单无抽成，超出45单的部分每单抽成6元，假设同一公司的“骑手”一日送餐单数相同，现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数，得到如下条形图：‎ ‎（Ⅰ）求百度外卖公司的“骑手”一日工资（单位：元）与送餐单数的函数关系；‎ ‎（Ⅱ）若将频率视为概率，回答下列问题：‎ ‎①记百度外卖的“骑手”日工资为（单位：元），求的分布列和数学期望；‎ ‎②小明拟到这两家公司中的一家应聘“骑手”的工作，如果仅从日收入的角度考虑，请你利用所学的统计学知识为他作出选择，并说明理由.‎ ‎20.已知矩形EFMN，，，以EF的中点O为原点，建立如图的平面直角坐标系，若椭圆以E，F为焦点，且经过M，N两点.‎ ‎（1）求椭圆方程；‎ ‎（2）直线与相交于A，B两点，在y轴上是否存在点C，使得△ABC为正三角形，若存在，求出l的方程；若不存在，说明理由.‎ ‎21.已知函数，‎ ‎（1）当时，求函数的单调区间；‎ ‎（2）记函数的导函数为，若函数存在两个小于零的零点，证明：.‎ 选修4-4：坐标系与参数方程 ‎22.在极坐标系中，曲线，直角坐标系中，直线l：（t为参数）（直角坐标系xOy与极坐标系有相同的长度单位，且以极点O为原点，极轴所在直线为x轴）.‎ ‎（1）求曲线C和直线l的直角坐标方程，并判断它们的位置关系；‎ ‎（2）若A，B为曲线C上两点，且，求的最大值.‎ 选修4-5：不等式选讲 ‎23.已知函数.‎ ‎（1）求不等式的解集；‎ ‎（2）若，证明：.‎ ‎2020届高三数学（理）“大题精练”6（答案解析）‎ ‎17.已知数列的前项和为，且.‎ ‎（1）求数列的通项公式；‎ ‎（2）记，求数列的前项和.‎ ‎【解】（1）当时，，得 当时，有，‎ 所以 即，满足时，， ‎ 所以是公比为2，首项为1的等比数列， ‎ 故通项公式为． ‎ ‎（2）， ‎ ‎ ．‎ ‎18.已知多面体ABCDEF中，四边形ABFE为正方形，，，G为AB的中点，.‎ ‎（1）求证：平面CDEF；‎ ‎（2）求平面ACD与平面BCF所成锐二面角的余弦值.‎ ‎【解】(1)证明：取中点,连接,根据题意可知,四边形是边长为2的正方形,所以,易求得,所以, 于是；‎ 而,所以平面,又因为,所以平面；‎ ‎(2)因为平面,且,故以为空间直角坐标系原点建立如图空间直角坐标系.‎ 由题意可知,故.‎ 设平面的法向量,则,即,‎ 不妨设,则易得.故.‎ 又,故可设平面的法向量.‎ 设平面与平面所成锐二面角为,故.‎ ‎19.美团外卖和百度外卖两家公司其“骑手”的日工资方案如下：美团外卖规定底薪70元，每单抽成1元；百度外卖规定底薪100元，每日前45单无抽成，超出45单的部分每单抽成6元，假设同一公司的“骑手”一日送餐单数相同，现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数，得到如下条形图：‎ ‎（Ⅰ）求百度外卖公司的“骑手”一日工资（单位：元）与送餐单数的函数关系；‎ ‎（Ⅱ）若将频率视为概率，回答下列问题：‎ ‎①记百度外卖的“骑手”日工资为（单位：元），求的分布列和数学期望；‎ ‎②小明拟到这两家公司中的一家应聘“骑手”的工作，如果仅从日收入的角度考虑，请你利用所学的统计学知识为他作出选择，并说明理由.‎ ‎【解】（I） ‎ ‎（II）‎ ‎100‎ ‎106‎ ‎118‎ ‎130‎ ‎0.2‎ ‎0.3‎ ‎0.4‎ ‎0.1‎ ‎（元）‚美团外卖“骑手”日平均送餐单数为：‎ 所以美团外卖“骑手”日平均工资为：（元）‎ 由知，百度外卖“骑手”日平均工资为112元. 故推荐小明去美团外卖应聘.‎ ‎20.已知矩形EFMN，，，以EF的中点O为原点，建立如图的平面直角坐标系，若椭圆以E，F为焦点，且经过M，N两点.‎ ‎（1）求椭圆方程；‎ ‎（2）直线与相交于A，B两点，在y轴上是否存在点C，使得△ABC为正三角形，若存在，求出l的方程；若不存在，说明理由.‎ ‎【解】(1)设椭圆的方程为,,‎ 则根据题意有,由椭圆的定义有,‎ ‎,故,所以.‎ 故椭圆的方程为.‎ ‎(2) 假设轴上存在点使得为等边三角形,设.‎ 中点为,则,.‎ 联立 ,整理得.‎ 则,解得.‎ 由韦达定理得,,‎ 故,‎ 又,,即,则直线的方程为,令,可得,即.‎ 又因为,故,‎ 即 .解得,满足.‎ 故轴上存在点使得为等边三角形,此时或 ‎21.已知函数，‎ ‎（1）当时，求函数的单调区间；‎ ‎（2）记函数的导函数为，若函数存在两个小于零的零点，证明：.‎ ‎【解】(1) 当时,,此时.‎ 令解得,令解得或,‎ 故的单调增区间为,单调减区间为与 ‎(2) 由题,有两个小于零的零点,故,解得.‎ 由题, 为的两根,故 又.‎ 故,.‎ 所以,‎ 代入韦达定理可得,‎ 化简得.‎ 又.‎ 因为,故.‎ 故欲证,即证,即证.‎ 设.即证.‎ 设函数 .‎ 故,故为增函数.‎ 故,即.‎ 故成立.‎ 选修4-4：坐标系与参数方程 ‎22.在极坐标系中，曲线，直角坐标系中，直线l：（t为参数）（直角坐标系xOy与极坐标系有相同的长度单位，且以极点O为原点，极轴所在直线为x轴）.‎ ‎（1）求曲线C和直线l的直角坐标方程，并判断它们的位置关系；‎ ‎（2）若A，B为曲线C上两点，且，求的最大值.‎ ‎【解】(1)由可得.‎ 又.‎ 故,.又圆心到的距离,故圆与直线相切.‎ ‎(2) 不妨设,,则 ‎.‎ 当,即时取最大值.‎ 选修4-5：不等式选讲 ‎23.已知函数.‎ ‎（1）求不等式的解集；‎ ‎（2）若，证明：.‎ ‎【解】（Ⅰ）依题意，‎ 由，解得，故．‎ ‎（Ⅱ）由（Ⅰ）可知，；‎ 因为 ，‎ 故，故．‎