2017-2018学年山西省阳高县第一中学高二下学期第一次月考数学（文）试题 Word版

2017-2018学年山西省阳高县第一中学高二下学期第一次月考数学（文）试题 Word版

2017-2018 学年山西省阳高县第一中学高二 下学期第一次月考数学（文） ( 总分：150 时间：120 分钟） 一、选择题（共 12 题，每小题 5 分） 1．在对两个变量 x，y 进行线性回归分析时有下列步骤： ①对所求出的回归方程作出解释；②收集数据(xi，yi)，i＝1,2，…， n；③求线性回归方程；④求相关系数；⑤根据所搜集的数据绘制散 点图． 如果根据可靠性要求能够作出变量 x，y 具有线性相关结论，则 下列操作顺序正确的是( ) A．①②⑤③④ B．③②④⑤① C．②④③①⑤ D．②⑤④③① 2.为了评价某个电视栏目的改革效果，在改革前后分别从居民点抽取了 100 位居民进行调查，经过计算 K2≈0.99，根据这一数据分析，下列说法正确的是 ( ) A.有 99%的人认为该电视栏目优秀 B.有 99%的人认为该电视栏目是否优秀与改革有关系 C.有 99%的把握认为该电视栏目是否优秀与改革有关系 D.没有理由认为该电视栏目是否优秀与改革有关系 3. 若函数 y=f(x)在区间(a，b)内可导，且 x0∈(a，b)，则的值为 ( ) A.f′(x0) B.2f′(x0) C.-2f′(x0) D.0 4. 若曲线 y=xα+1(α∈R)在(1，2)处的切线经过原点，则α=( ) A.1 B.2 C.3 D.4 5．f(x)＝ax3＋2 x，若 f′(1)＝4，则 a 的值等于( ) A.1 2 B.1 3 C. 2 D．1 6．若 f(n)＝1＋1 2 ＋1 3 ＋…＋ 1 2n＋1(n∈N*)，则当 n＝2 时，f(n)是( )． A．1＋1 2 B.1 5 C．1＋1 2 ＋1 3 ＋1 4 ＋1 5 D．非以上答案 7. 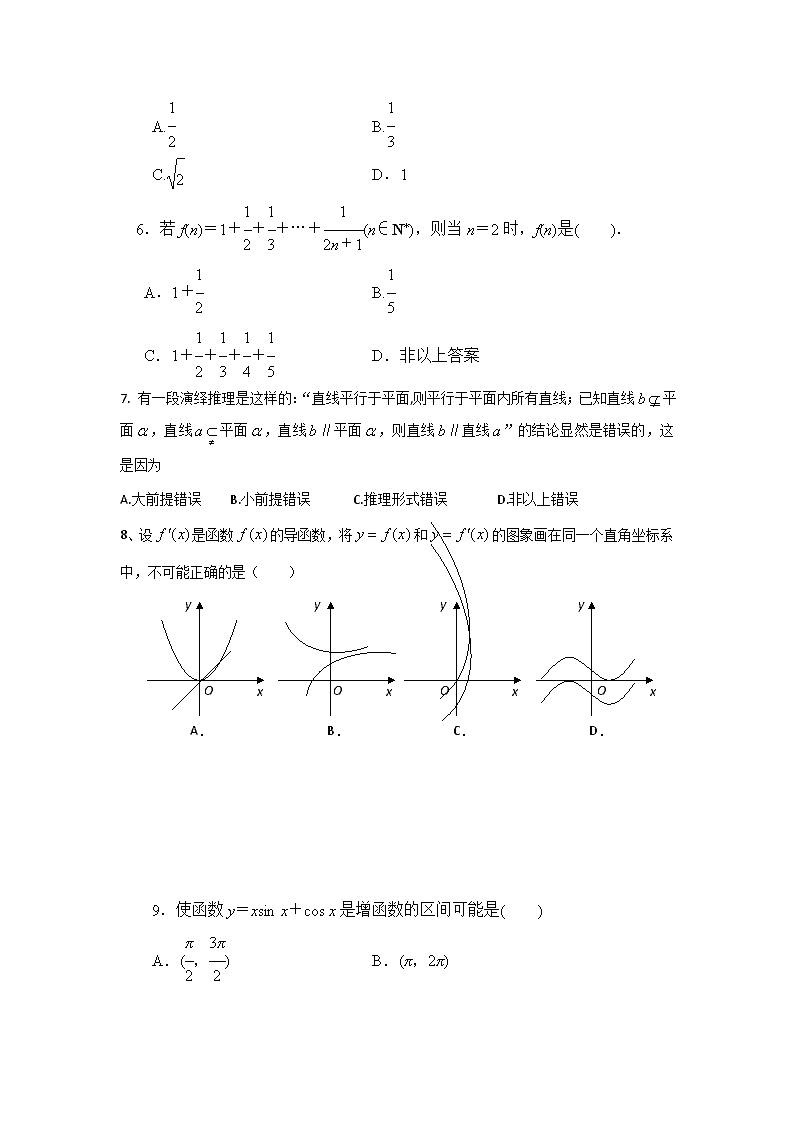有一段演绎推理是这样的：“直线平行于平面,则平行于平面内所有直线；已知直线b  平 面 ，直线 a   平面 ，直线 b ∥平面 ，则直线 b ∥直线 a ”的结论显然是错误的，这 是因为 A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误 8、设 ( )f x 是函数 ( )f x 的导函数，将 ( )y f x 和 ( )y f x 的图象画在同一个直角坐标系 中，不可能正确的是（ ） 9．使函数 y＝xsin x＋cos x 是增函数的区间可能是( ) A．(π 2 ，3π 2 ) B．(π，2π) C．(3π 2 ，5π 2 ) D．(2π，3π) 10．一汽车沿直线轨道前进，刹车后列车速度为 v(t)＝18－6t，则列车的刹 车距离为( ) y xO y xO y xO y xO A． B． C． D． A．27 B．54 C．81 D．13.5 图 1 11．设函数 f(x)在 R 上可导，其导函数为 f′(x)，且函数 y＝(1－x)f′(x)的 图象如图 1 所示，则下列结论中一定成立的是( ) A．函数 f(x)有极大值 f(2)和极小值 f(1) B．函数 f(x)有极大值 f(－2)和极小值 f(1) C．函数 f(x)有极大值 f(2)和极小值 f(－2) D．函数 f(x)有极大值 f(－2)和极小值 f(2) 12．已知三次函数 f(x)＝1 3x3－(4m－1)x2＋(15m2－2m－7)x＋2 在 x∈(－∞，＋∞)是增函 数，则 m 的取值范围是( ) A．m<2 或 m>4 B．－41 时，1 2x2＋lnx<2 3x3. 高二数学（文） ( 总分：150 时间：120 分钟） 三、选择题（共 12 题，每小题 5 分） 1．答案：D 2.答案：C 3【解析】选 B. 4.【解析】选 B. 5．【答案】 D 6．答案 C 7.答案 A 8、答案：D 9．【答案】 C 10．【答案】 A 【答案】 D 12．[答案] D 四、 填空题（共 4 小题，每小题 5） 13．答案 ①② 14: (0) 1f  15．[答案] 2 3 ＋ln2 16、【答案】 2 1y x   三、解答题(共 6 题) 17．利用导数和三段论证明：函数 xxxf 2)( 2  在（-∞，1）上是增函数。（必须 用三段论，否则 0 分） 18．周长为 20 cm 的矩形，绕一条边旋转成一个圆柱，求圆柱体积的最大值 为。 【解析】 设矩形的长为 x，则宽为 10－x(00，当 x∈(20 3 ，10)时，V′(x)<0， ∴当 x＝20 3 时，V(x)取得最大值为4 000 27 π cm3. 【答案】 4 000 27 π cm3 19．(本题满分 12 分)设函数 f(x)＝x3－3ax＋b(a≠0)． (1)若曲线 y＝f(x)在点(2，f(2))处与直线 y＝8 相切，求 a，b 的值； (2)求函数 f(x)的单调区间与极值点． [分析] 考查利用导数研究函数的单调性，极值点的性质，以及分类讨论思想． [解析] (1)f′(x)＝3x2－3a. 因为曲线 y＝f(x)在点(2，f(2))处与直线 y＝8 相切， 所以 f′(2)＝0， f(2)＝8. 即 3(4－a)＝0， 8－6a＋b＝8. 解得 a＝4，b＝24. (2)f′(x)＝3(x2－a)(a≠0)． 当 a<0 时，f′(x)>0，函数 f(x)在(－∞，＋∞)上单调递增，此时函数 f(x)没有极值 点． 当 a>0 时，由 f′(x)＝0 得 x＝± a. 当 x∈(－∞，－ a)时，f′(x)>0，函数 f(x)单调递增； 当 x∈(－ a， a)时，f′(x)<0，函数 f(x)单调递减； 当 x∈( a，＋∞)时，f′(x)>0，函数 f(x)单调递增． 此时 x＝－ a是 f(x)的极大值点，x＝ a是 f(x)的极小值点． 20. （本小题满分 12 分） 某地区 2007 年至 2013 年农村居民家庭纯收入 y（单位：千元）的数据如下表： 年份 2007 2008 2009 2010 2011 2012 2013 年份代号 t 1 2 3 4 5 6 7 人均纯收入 y 2.9 3.3 3.6 4.4 4.8 5.2 5.9 （Ⅰ）求 y 关于 t 的线性回归方程； （Ⅱ）利用（Ⅰ）中的回归方程，分析 2007 年至 2013 年该地区农村居民家庭人均纯收入的 变化情况，并预测该地区 2015 年农村居民家庭人均纯收入. 附：回归直线的斜率和截距的最小二乘法估计公式分别为：      1 2 1 n i i i n i i t t y y b t t          ， ˆˆa y bt  【答案】 (1) .3.25.0 += ty （2） 约 6800 元 【解析】 （1） .3.25.0 3.24*2 1-3.4- ,2 1 2*14 14 2*)149( 8.48.15.007.0214*3 , 3.47 9.52.58.44.46.33.39.2,47 721 += === ==++ ++++++= += =++++++==+++= tyty tbya b abty yt 的回归方程为关于所以， 代入公式，经计算得设回归方程为  21.（12 分） 海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了 100 个网 箱，测量各箱水产品的产量（单位：kg）, 其频率分布直方图如下： D． 记 A 表示事件“旧养殖法的箱产量低于 50kg”，估计 A 的概率； E． 填写下面列联表，并根据列联表判断是否有 99%的把握认为箱产量与养殖方法有关： 箱产量＜50kg 箱产量≥50kg 旧养殖法 新养殖法 F． 根据箱产量的频率分布直方图，对两种养殖方法的优劣进行较。 附： P（） 0.050 0.010 0.001 k 3.841 6.635 10.828 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d      【答案】（1）0.62.（2）有把握（3）新养殖法优于旧养殖法 试题解析：（1）旧养殖法的箱产量低于 50kg 的频率为 （0.012+0.014+0.024+0.034+0.040）×5=0.62 因此，事件 A 的概率估计值为 0.62. (2)根据箱产量的频率分布直方图得列联表 箱产量＜50kg 箱产量≥50kg 旧养殖法 62 38 新养殖法 34 66 K2= 200 66-34 38 15.705100 100 96 104       （62 ）≈ 由于 15.705＞6.635,故有 99%的把握认为箱产量与养殖方法有关. (3)箱产量的频率分布直方图平均值(或中位数)在45kg到50kg之间,且新养殖法的箱产量分 布集中程度较旧养殖法的箱产量分布集中程度高,因此,可以认为新养殖法的箱产量较高且 稳定,从而新养殖法优于旧养殖法. 【考点】频率分布直方图 【名师点睛】（1）频率分布直方图中小长方形面积等于对应概率，所有小长方形面积之和为 1； （2）频率分布直方图中均值等于组中值与对应概率乘积的和 （3）均值大小代表水平高低，方差大小代表稳定性 22．(本题满分 12 分)已知函数 f(x)＝1 2 x2＋lnx. (1)求函数 f(x)的单调区间； (2)求证：当 x>1 时，1 2 x2＋lnx<2 3 x3. [解析] (1)依题意知函数的定义域为{x|x>0}， ∵f′(x)＝x＋1 x ，故 f′(x)>0， ∴f(x)的单调增区间为(0，＋∞)． (2)设 g(x)＝2 3 x3－1 2 x2－lnx， ∴g′(x)＝2x2－x－1 x ， ∵当 x>1 时，g′(x)＝(x－1)(2x2＋x＋1) x >0， ∴g(x)在(1，＋∞)上为增函数， ∴g(x)>g(1)＝1 6 >0， ∴当 x>1 时，1 2 x2＋lnx<2 3 x3.