2017-2018学年江苏省东台市第一中学高二上学期期中考试数学试题 缺答案

2017-2018学年江苏省东台市第一中学高二上学期期中考试数学试题 缺答案

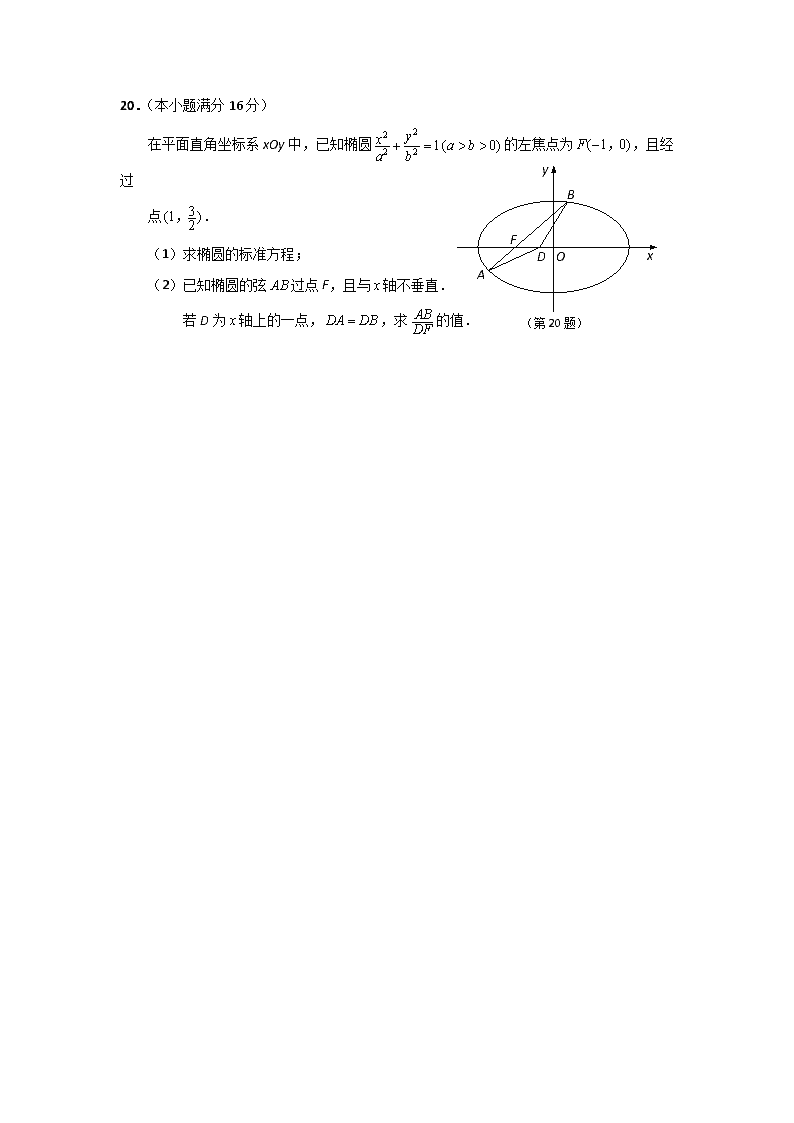
东台市第一中学2017—2018学年度第一学期期中考试 高二数学试卷 一、填空题：（本大题共14小题，每小题5分，共70分.把每小题的答案填在答题纸相应的位置上）‎ ‎1. 抛物线的焦点坐标是______▲________.‎ ‎2. “＜0，使＞‎0”‎的否定是 ▲ .‎ ‎3. 双曲线的渐近线方程是 ▲ . ‎ ‎4. 命题“若，则”的否命题为 ▲ .‎ ‎5. “x＞‎0”‎是“x＞‎1”‎成立的　 ▲ 　条件（在“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中选出一种）‎ ‎6. 不等式的解集为 ▲ .‎ ‎7. 若实数x，y满足则不等式组表示的区域面积为____▲____.‎ ‎8. 已知不等式的解集为，则 ▲ .‎ ‎9. 若F1,F2是椭圆 的两个焦点，过F1作直线与椭圆交于A,B两点，则 的周长为________▲_______.‎ ‎10. 已知，则的最小值为 ▲ .‎ ‎11. 已知x, y为正实数，且则的最小值为 ▲ .‎ ‎12. 椭圆短轴上的两个三等分点与两个焦点构成一个正方形，则椭圆的离心率为 ▲ .‎ ‎13. 已知点是椭圆的左焦点和上顶点，若点是椭圆上一动点，则周长的最大值为 ▲ ． ‎ ‎14. 已知a，t为正实数，函数f(x)=x2-2x+a，且对任意的x∈[0，t]，都有f(x)∈[-a，a].若对每一个正实数a，记t的最大值为g(a)，则函数g(a)的值域为　　▲ 　　.‎ 二、解答题（本大题共6小题，共90分．解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎15．（本题满分14分）命题：关于的不等式，对一切恒成立，命题：指数函数在R为增函数，若为真，为假，求实数的取值范围.‎ ‎16．（本题满分14分）已知不等式的解集A；关于的不等式的解集为，（1）求A （2）若，求实数的取值范围．‎ ‎17. （本题满分15分）求适合下列条件的圆锥曲线的标准方程.‎ ‎（1）准线方程为x=-1的抛物线;‎ ‎（2）离心率为，准线方程为的椭圆;‎ ‎（3）焦点在y轴上，一条渐近线方程为，实轴长为12.‎ ‎18. （本题满分15分）投资生产A产品时，每生产100t需要资金200万元，需场地‎200m2‎，可获利润300万元；投资生产B产品时，每生产‎100m需要资金300万元，需场地‎100m2‎，可获利润200万元。现某单位可使用资金1400万元，场地‎900m2‎，问：应作怎样的组合投资，可使获利最大？‎ ‎19. （本题满分16分）某工厂建造一个无盖的长方体贮水池，其容积为‎4800m3‎，深度为‎3m，如果池底每‎1m2‎的造价为150元，池壁每‎1m2‎的造价为120元。‎ ‎（1）设池底的一边长为x m，总造价为f(x)元，求f(x)的解析式；‎ ‎（2）怎样设计水池能使总造价最低？最低总造价为多少元？‎ ‎20．（本小题满分16分）‎ A B D O x y ‎（第20题）‎ F 在平面直角坐标系xOy中，已知椭圆的左焦点为，且经过 点． ‎ ‎（1）求椭圆的标准方程；‎ ‎ （2）已知椭圆的弦过点F，且与轴不垂直．‎ 若D为轴上的一点，，求的值．‎