高考数学专题复习：温州中学2012学年第一学期期末考试（理科）

高考数学专题复习：温州中学2012学年第一学期期末考试（理科）

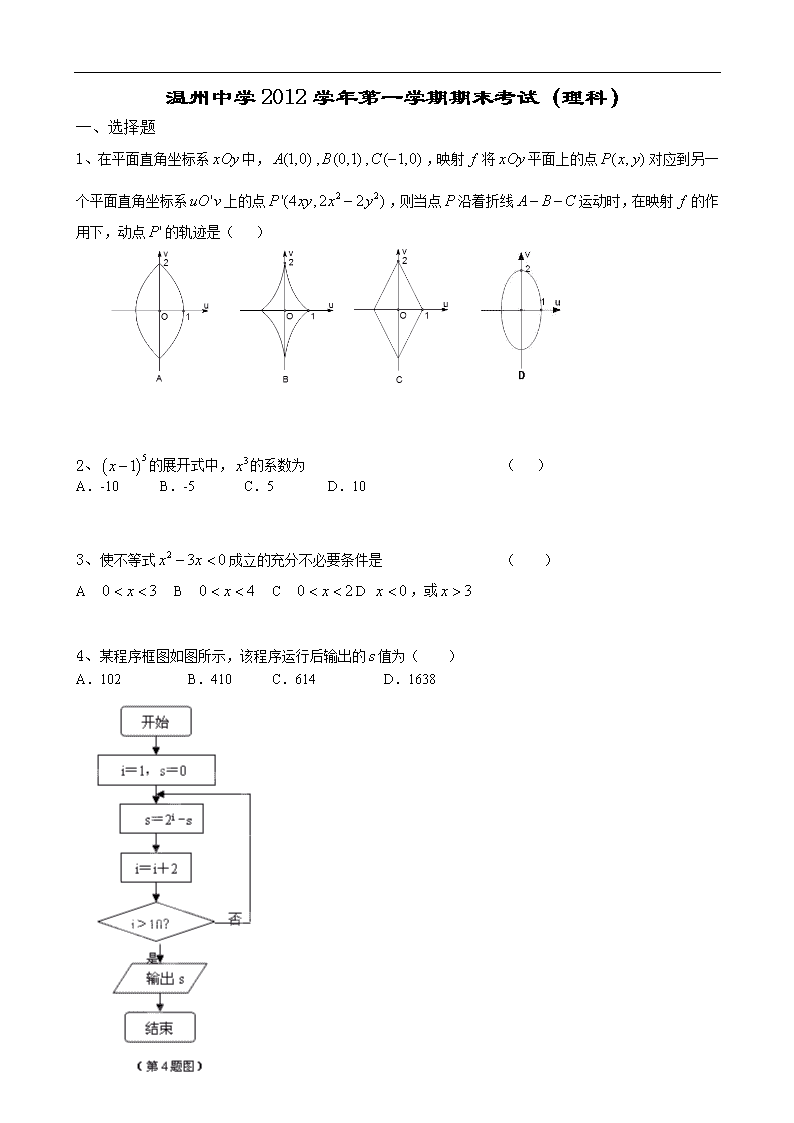
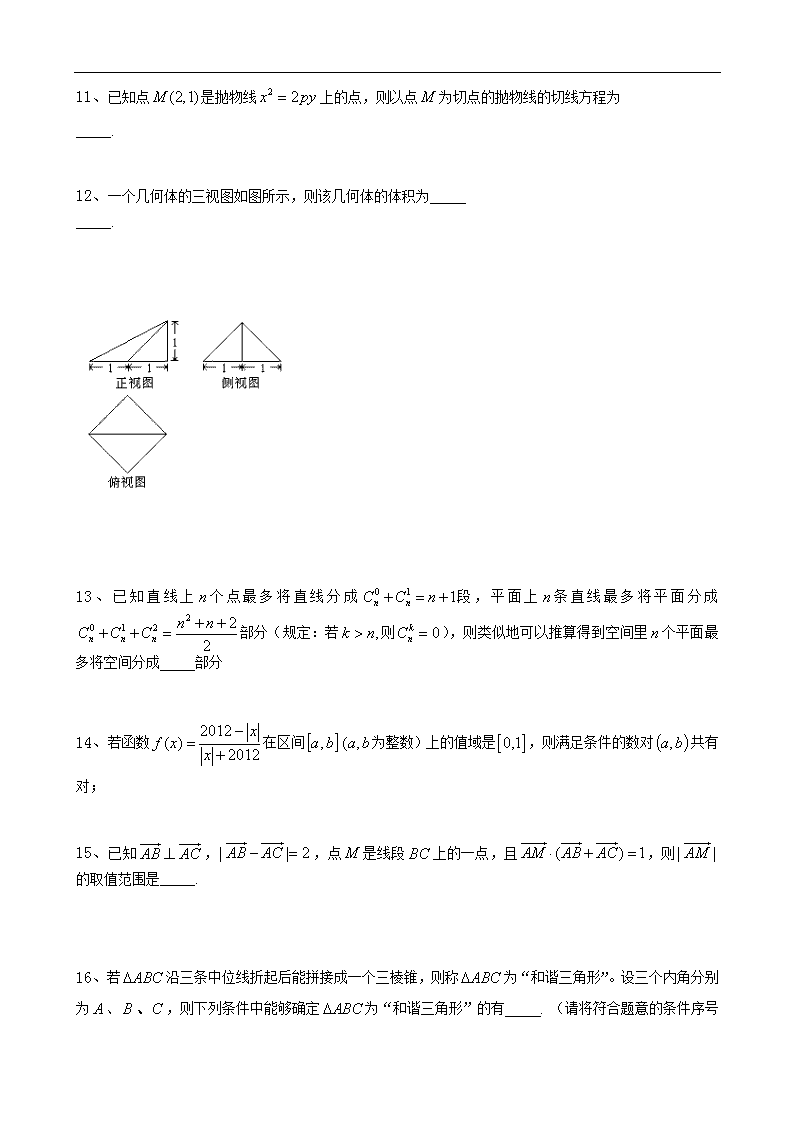
温州中学2012学年第一学期期末考试（理科）‎ 一、选择题 ‎1、在平面直角坐标系中，，映射将平面上的点对应到另一个平面直角坐标系上的点，则当点沿着折线运动时，在映射的作用下，动点的轨迹是（ ）‎ ‎ ‎ ‎2、的展开式中，的系数为 （ ）‎ A．-10 B．‎-5 C．5 D．10 ‎ ‎3、使不等式成立的充分不必要条件是 （ ）‎ A B C D ，或 ‎4、某程序框图如图所示，该程序运行后输出的值为（ ） ‎ A．102 B．‎410 ‎ C．614 D．1638‎ ‎5、设是三个不重合的平面，是不重合的直线，下列判断正确的是 （ ）‎ A．若则 B．若则 C．若则 D．若则 ‎6、已知，且，则为（ ）‎ A. B. C. D. ‎ ‎7、已知双曲线：，左右焦点分别为，过的直线交双曲线左支于两点，则的最小值 为（ ）‎ A. B. ‎11 C.12 D.16 ‎ ‎8、已知不等式对于，恒成立，则实数的取值范围（ ）‎ A． B． C． D． ‎ ‎9、设等差数列的前项和为,若,则满足的正整数的值为（ ） ‎ A.10 B‎.11 C.12 D. 13‎ ‎10、若，其中，是虚数单位，则 （ ）‎ A．-3 B．‎-2 ‎ C．2 D．3‎ 二、填空题 ‎11、已知点是抛物线上的点，则以点为切点的抛物线的切线方程为 ‎ .‎ ‎12、一个几何体的三视图如图所示，则该几何体的体积为 ‎ ‎ .‎ ‎13、已知直线上个点最多将直线分成段，平面上条直线最多将平面分成部分（规定：若则），则类似地可以推算得到空间里个平面最多将空间分成 部分 ‎14、若函数在区间为整数）上的值域是，则满足条件的数对共有 对；‎ ‎15、已知，，点是线段上的一点，且，则的取值范围是 .‎ ‎16、若沿三条中位线折起后能拼接成一个三棱锥，则称为“和谐三角形”。设三个内角分别为、、，则下列条件中能够确定为“和谐三角形”的有 .‎ ‎ （请将符合题意的条件序号都填上）‎ ‎①； ②；‎ ‎③； ④。‎ ‎17、一个袋子里装有大小相同的3个红球和2个黄球，从中同时取出2个球，则其中含红球个数的数学期望是 .‎ 三、解答题 ‎18、 已知函数 ‎（1）当时，试判断函数的单调性；‎ ‎（2）当时，对于任意的，恒有，求的最大值．‎ ‎19、已知， 且.‎ ‎（1）求；‎ ‎（2）当时，求函数的值域.‎ ‎20、已知数列，，且，‎ ‎（1）若成等差数列，求实数的值；（2）数列能为等比数列吗？若能，‎ 试写出它的充要条件并加以证明；若不能，请说明理由。‎ ‎21、如图，几何体为正四棱锥，几何体为正四面体.‎ ‎（1）求证：；‎ ‎（2）求与平面所成角的正弦值.‎ ‎22、已知抛物线的焦点F到直线的距离为．‎ ‎（1）求抛物线的方程；‎ ‎（2）如图，过点F作两条直线分别交抛物线于A、B和C、D，过点F作垂直于轴的直线分别交和于点.‎ 求证：．‎ 以下是答案 一、选择题 ‎1、A 二：填空题。‎ ‎2、D ‎ ‎3、C ‎ ‎4、B ‎ ‎5、B ‎ ‎6、D ‎ ‎7、B ‎8、A ‎ ‎9、C ‎ ‎10、D ‎ 二、填空题 ‎11、 ‎ ‎12、 ‎ ‎13、 ‎ ‎14、4025 ‎ ‎15、 ‎ ‎16、①③‎ 三：解答题。‎ ‎17、 ‎ 三、解答题 ‎18、解：（1）‎ 当时，，，故在区间，上单调递增，在上单调递减；‎ 当时，，，故在区间，上单调递增，在上单调递减；‎ 当时，恒有，‎ 当时，在，上单调递增，在上单调递减；‎ 当时，在区间上单调递增 当时，在，上单调递增，在上单调递减；‎ ‎（2）‎ 解法一：设函数，即在上恒成立。即为的最小值。。‎ 故在区间上单调递减，在区间单调递增。‎ 故，‎ 解法二：即与点连线斜率的最小值在时取到。设 则，即，‎ 又，故 ‎ ‎ ‎19、‎ 解：（1）因为，‎ 所以，又，故 ‎（2）由（1）得，‎ ‎ ㈠ 所以 ‎ ‎ 因为，所以 即，即 ‎ 因此，函数的值域为 ‎20、解.（Ⅰ），‎ 因为，所以，得 ‎（Ⅱ）方法一：因为，所以，‎ 得：，故是以为首项，‎ ‎-1为公比的等比数列，‎ 所以，得：‎ 为等比数列为常数，易得当且仅当时，为常数。‎ 方法二：因为，所以，‎ 即，故是以为首项，-2为公比的成等比数列，‎ 所以，得：（下同解法一）‎ 方法三：由前三项成等比得，进而猜测，对于所有情况都成立，再证明。‎ ‎21、 （1）解法一:取的中点，连结，由几何体为正四面体得，，所以平面，从而.‎ 连结交于点,连结得平面,‎ ‎，所以平面，从而.又 所以平面，从而.‎ 解法二: 因为几何体为正四棱锥，几何体为正四面体.‎ 故可设 取的中点，连结，由题意知 故是二面角的平面角， 是二面角的平面角,‎ 在中，，‎ 所以，‎ 在中，，‎ 所以 从而，从而四点共面，‎ 故四边形为菱形，从而 ‎（2）由解法二知四边形为菱形，于是，∥，‎ 所以点到平面的距离等于点到平面的距离，‎ 设点到平面的距离为，由得：‎ 进而得，所以与平面所成角的正弦值 ‎ ‎ 解法三：如图，以OB为x轴，OC为y轴，OP为z轴建立空间直角坐标系。‎ 不妨设|OB|=1，则B(1,0,0)，C(0,1,0)， D(-1,0,0)，A(0,-1,0) ‎ 因为为正四面体，所以为正三角形，所以，所以，因此P(0,0,1)。‎ 设的重心为M，则面PCB，又也为正三棱锥，因此面PCB，因此O、M、Q三点共线，所以OQ垂直面PCB，即是平面PCB的一个法向量，‎ 由，易得平面PCB的一个法向量可以取，所以不妨设Q(a,a,a)，则，因为解得a=1，所以Q(1,1,1)。‎ ‎（1），，，所以；‎ ‎（2）设面PAD的一个法向量为，，，由 解得一个法向量，‎ 所以，‎ 所以QD与平面PAD所成角的正弦值为。‎ ‎22、 解：（1）焦点，由已知得，且，解得，‎ 故所求抛物线的方程为.‎ ‎（2）设直线的方程为：，‎ 直线的方程为：，‎ 令 将两条直线的方程代入抛物线方程得：‎ 于是有： ，‎ 同理得： ，‎ 故 ‎ ，同理 所以直线的方程为：， ①‎ 直线的方程为：， ②‎ 将代入①式得：‎ 将代入②式得：‎ 所以，即