2018-2019学年内蒙古包头市第四中学高二上学期第二次月考数学（理）试题 Word版

2018-2019学年内蒙古包头市第四中学高二上学期第二次月考数学（理）试题 Word版

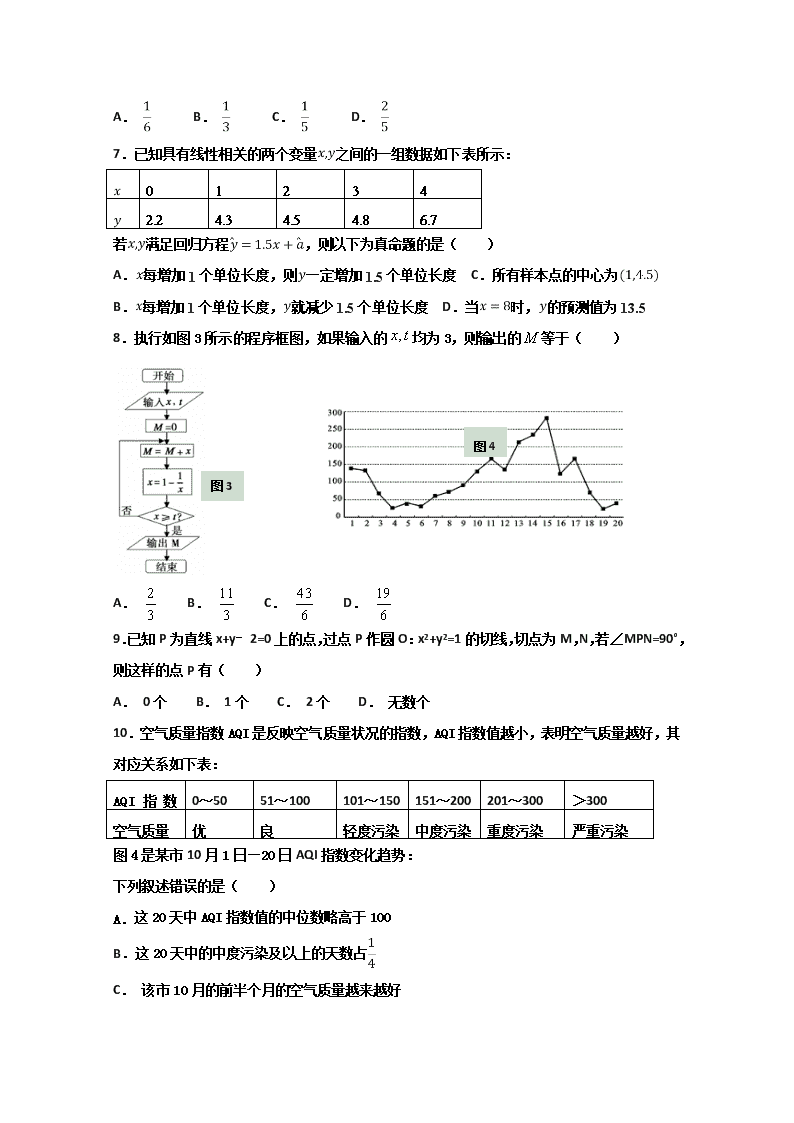
包头四中2018-2019学年第一学期第二次月考 高二年级数学（理科）试题 满分：150分 考试时间：120分钟 一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．下列命题正确的是（ ）‎ A． B． 是的充分不必要条件 C． D． 若，则 ‎2．2017年3月2日至16日，全国两会在北京召开，甲、乙两市近5年与会代表名额数统计如图1所示，设甲、乙的数据平均数分别为，中位数分别为y1，y2，则（　　）‎ 图2‎ 图1‎ ‎ ‎ A． ，y1＞y2 B． ，y1=y2 ‎ C． ，y1=y2 D． ，y1＜y2‎ ‎3．已知随机变量服从正态分布,且( )‎ A． 0.6 B． 0.4 C． 0.3 D． 0.2‎ ‎4．如图2，是上一点，分别以为直径作半圆．从作，与半圆相交于．，在整个图形中随机取一点，则此点取自图中阴影部分的概率是（ ）‎ A． B． C． D． ‎ ‎5．我国古代数学名著《九章算术》中有如下问题“今有北乡八千七百五十八，西乡七千二百三十六，南乡八千三百五十六，凡三乡，发役三百七十八人，欲以算数多少出之，何各几何？”意思是：北乡有8758人，西乡有7236人，南乡有8356人，现要按人数多少从三乡共征集378人，问从各乡征集多少人？在上述问题中，需从西乡征集的人数是 （ ）‎ A． 102 B． 112 C． 130 D． 136‎ ‎6．箱子里有3双颜色不同的手套（红蓝黄各1双），有放回地拿出2只，记事件A表示“拿出的手套一只是左手的，一只是右手的，但配不成对”，则事件A的概率为（　　）‎ A． B． C． D． ‎ ‎7．已知具有线性相关的两个变量之间的一组数据如下表所示：‎ 0 1 2 3 4 2.2 4.3 4.5 4.8 6.7 若满足回归方程，则以下为真命题的是（ ）‎ A．每增加1个单位长度，则一定增加1.5个单位长度 C．所有样本点的中心为 B．每增加1个单位长度，就减少1.5个单位长度 D．当时，的预测值为13.5‎ ‎8．执行如图3所示的程序框图，如果输入的均为3，则输出的等于（ ）‎ 图4‎ 图3‎ ‎ ‎ A． B． C． D． ‎ ‎9．已知P为直线x+y﹣2=0上的点，过点P作圆O：x2+y2=1的切线，切点为M，N，若∠MPN=90°，则这样的点P有（　　）‎ A． 0个 B． 1个 C． 2个 D． 无数个 ‎10．空气质量指数AQI是反映空气质量状况的指数，AQI指数值越小，表明空气质量越好，其对应关系如下表：‎ AQI指数值 ‎0～50‎ ‎51～100‎ ‎101～150‎ ‎151～200‎ ‎201～300‎ ‎＞300‎ 空气质量 优 良 轻度污染 中度污染 重度污染 严重污染 图4是某市10月1日—20日AQI指数变化趋势：‎ 下列叙述错误的是（ ）‎ A． 这20天中AQI指数值的中位数略高于100 ‎ B．这20天中的中度污染及以上的天数占 C． 该市10月的前半个月的空气质量越来越好 D． 总体来说，该市10月上旬的空气质量比中旬的空气质量好 ‎11．某单位青年、中年、老年职员的人数之比为10∶8∶7，从中抽取200名职员作为样本，若每人被抽取的概率是0.2，则该单位青年职员的人数为(　　)‎ A． 280 B． 320 C． 400 D． 1000‎ ‎12．已知圆C：x2+y2=4，直线l:x+y=m（mR），设圆C上到直线l的距离为1的点的个数为S，当0≤m<3时，则S的可能取值共有（ ）‎ A． 2种 B． 3种 C． 4种 D． 5种 二、填空题：本题共4小题，每小题5分，共20分.‎ ‎13．如果数据的平均数为，方差为，则的方差为_______.‎ ‎14．每年的9月初是高校新生到校报道的时间，此时学生会将组织师兄师姐做好迎接接待工作，若某学院只有3位师兄在迎新现场，突然来了4位新生，要求一次性派发完迎新指引工作（可以有1位师兄接待2位新生），则安排方案有______种．（用数字作答）‎ ‎15．在平面直角坐标系xOy中，已知过点的圆和直线 相切，且圆心在直线 上，则圆C的标准方程为__________________．‎ ‎16．的展开式中的系数是_________(用数字作答).‎ 三、 解答题：共70分.解答题应写出文字说明、证明过程或演算步骤.‎ ‎17．(10分)已知命题：方程有实根，命题：－1≤≤5．若为假命题，为真命题，求实数的取值范围．‎ ‎18．(12分)2018年8月8日是我国第十个全民健身日，其主题是：新时代全民健身动起来．某市为了解全民健身情况，随机从某小区居民中抽取了40人，将他们的年龄分成7段：[10, 20)，[20, 30)，[30, 40)，[40, 50)，[50, 60)，[60, 70)，[70, 80]后得到如图所示的频率分布直方图．‎ ‎（1）试求这40人年龄的平均数、中位数的估计值；‎ ‎（2）（i）若从样本中年龄在[50, 70)的居民中任取2人赠送健身卡，求这2人中至少有1人年龄不低于60岁的概率；‎ ‎（ii）已知该小区年龄在[10, 80]内的总人数为2000，若18岁以上（含18岁）为成年人，试估计该小区年龄不超过80岁的成年人人数．‎ ‎19．(12分)柴静《穹顶之下》的播出，让大家对雾霾天气的危害有了更进一步的认识，对于雾霾天气的研究也渐渐活跃起来，某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析，得出下表数据：‎ x ‎4‎ ‎5‎ ‎7‎ ‎8‎ y ‎2‎ ‎3‎ ‎5‎ ‎6‎ ‎(1)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；‎ ‎(2)试根据(1)求出的线性回归方程，预测燃放烟花爆竹的天数为9的雾霾天数．‎ 参考公式：，，其中，为数据x，y的平均数．‎ ‎20．(12分)“微信运动”已成为当下热门的健身方式，小王的微信朋友圈内也有大量好友参与了“微信运动”，他随机选取了其中的40人（男、女各20人），记录了他们某一天的走路步数，并将数据整理如下：‎ ‎（1）若采用样本估计总体的方式，试估计小王的所有微信好友中每日走路步数超过5000步的概率；‎ ‎（2）已知某人一天的走路步数超过8000步被系统评定“积极型”，否则为“懈怠型”，根据题意完成下面的列联表，并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关？‎ ‎21．(12分)甲同学参加化学竞赛初赛，考试分为笔试、口试、实验三个项目，各单项通过考试的概率依次为、、，笔试、口试、实验通过考试分别记4分、2分、4分，没通过的项目记0分，各项成绩互不影响. （Ⅰ）若规定总分不低于8分即可进入复赛，求甲同学进入复赛的概率；‎ ‎（Ⅱ）记三个项目中通过考试的个数为，求随机变量的分布列和数学期望.‎ ‎22.(12分)在平面直角坐标系中，曲线与坐标轴的交点都在圆上．（1）求圆的方程；（2）若圆与直线交于，两点，且，求的值．‎ 参考答案 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ B B C C B B D D B C C B 13． ‎ 1600 14．36 15． 16． ‎ ‎17．‎ ‎【详解】‎ 命题为真：因为方程有实根，所以，‎ 因为为假命题，为真命题，所以p,q一真一假，‎ 因此.‎ ‎18．(1) 中位数为35;(2) （ⅰ）;（ⅱ）该小区年龄不超过80岁的成年人人数约为2000×0.88＝1760．‎ ‎19．‎ ‎【详解】‎ ‎(1)[]‎ ‎， ‎ ‎，，‎ ‎， ‎ ‎，，‎ 故线性回归方程为. ‎ ‎(2)由(2)，当时，，即预测燃放烟花爆竹的天数为9的雾霾天数为7.‎ ‎20．‎ 试题解析：‎ ‎（1）由题知，40人中该日走路步数超过5000步的有35人，频率为，‎ 所以估计他的所有微信好友中每日走路步数超过5000步的概率为；‎ ‎（2），‎ 故没有95%以上的把握认为二者有关.‎ ‎21．‎ 试题解析：（Ⅰ）记笔试、口试、实验独立通过考试分别为事件，‎ 则事件“甲同学进入复赛的”表示为.‎ ‎∵与互斥，且彼此独立，‎ ‎∴.‎ ‎（Ⅱ）随机变量的所有可能取值为0,1,2,3.‎ ‎，‎ ‎ ，‎ ‎ ，‎ ‎.‎ 所以，随机变量的分布列为 数学期望.‎ ‎22．（1）曲线与轴的交点为，与轴的交点为 ‎ ．故可设的圆心为，则有，解得．则圆的半径为，所以圆的方程为．‎ ‎（2）设，，其坐标满足方程组 消去，得方程．‎ 由已知可得，判别式，且，．  由于，可得．‎ 又，‎ 所以． ‚ ‎ 由‚得，满足，故．‎