高考数学专题复习：《算法案例》同步训练题

高考数学专题复习：《算法案例》同步训练题

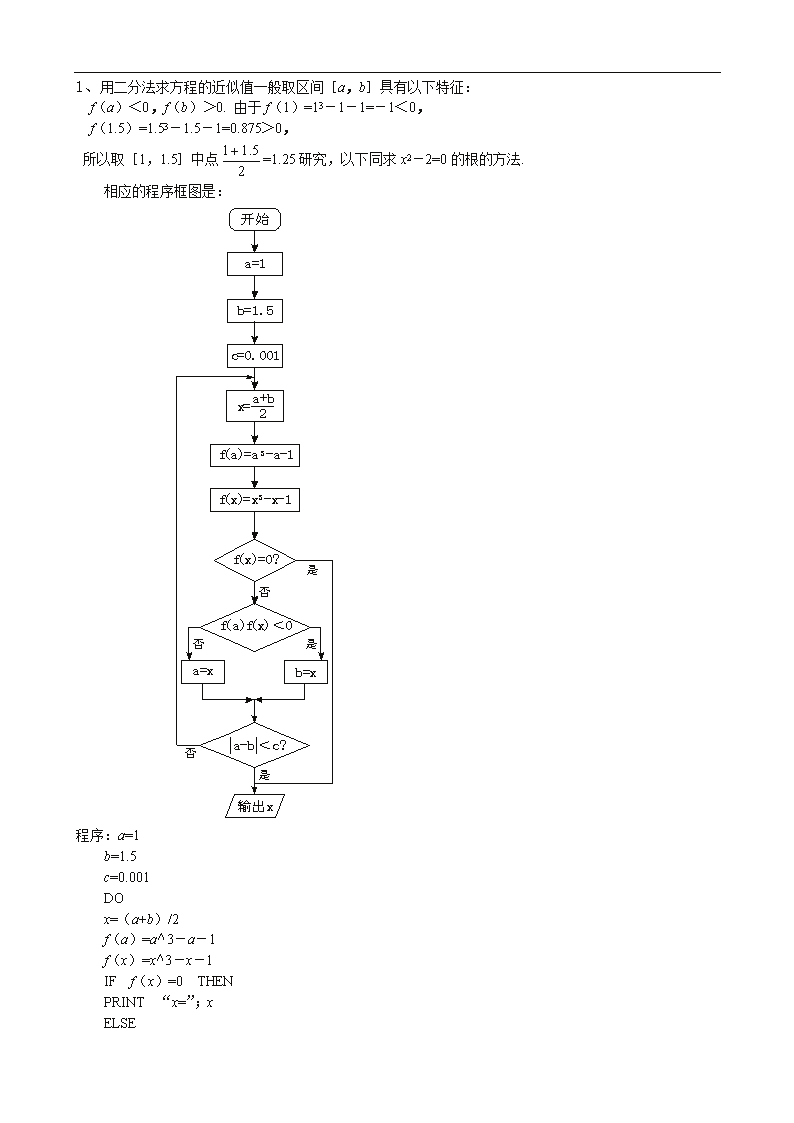
‎《算法案例》同步训练题 一、解答题 ‎1、写出用二分法求方程x3－x－1=0在区间［1，1.5］上的一个解的算法（误差不超过0.001），并画出相应的程序框图及程序. ‎ ‎2、我国古代数学家张邱建编《张邱建算经》中记有有趣的数学问题：“今有鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一凡百钱，买鸡百只，问鸡翁、母、雏各几何？”你能用程序解决这个问题吗？‎ ‎3、我国《算经十书》之一《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二.问物几何？答曰：二十三.”你 能用程序解决这个问题吗？‎ ‎4、用秦九韶算法写出求f（x）=1+x+0.5x2+0.16667x3+0.04167x4+0.00833x5‎ 在x=－0.2时的值的过程.‎ ‎5、用冒泡排序法将下列各数排成一列：8，6，3，18，21，67，54.‎ 并写出各趟的最后结果及各趟完成交换的次数.‎ ‎6、（1）将101111011（2）转化为十进制的数； ‎ ‎（2）将53（8）转化为二进制的数.‎ 以下是答案 一、解答题 ‎1、用二分法求方程的近似值一般取区间［a，b］具有以下特征：‎ f（a）＜0，f（b）＞0. 由于f（1）=13－1－1=－1＜0，‎ f（1.5）=1.53－1.5－1=0.875＞0，‎ 所以取［1，1.5］中点=1.25研究，以下同求x2－2=0的根的方法.‎ 相应的程序框图是：‎ 程序：a=1‎ b=1.5‎ c=0.001‎ DO x=（a+b）/2‎ f（a）=a∧3－a－1‎ f（x）=x∧3－x－1‎ IF f（x）=0 THEN PRINT “x=”；x ELSE IF f（a）*f（x）＜0 THEN b=x ELSE a=x END IF END IF LOOP UNTIL ABS（a－b）＜=c PRINT “方程的一个近似解x=”；x END ‎2、设鸡翁、母、雏各x、y、z只，则 由②，得z=100－x－y， ③‎ ‎③代入①，得5x+3y+=100，‎ ‎7x+4y=100. ④‎ 求方程④的解，可由程序解之.‎ 程序：x=1‎ y=1‎ WHILE x＜=14‎ WHILE y＜=25‎ IF 7*x+4*y=100 THEN z=100－x－y PRINT “鸡翁、母、雏的个数别为：”；x，y，z END IF y=y+1‎ WEND ‎ x=x+1‎ y=1‎ WEND END ‎（法二）实际上，该题可以不对方程组进行化简，通过设置多重循环的方式得以实现.由①、②可得x最大值为20，y最大值为33，z最大值为100，且z为3的倍数.程序如下：‎ x=1‎ y=1‎ z=3‎ WHILE x＜=20‎ WHILE y＜=33‎ WHILE z＜=100‎ IF 5*x+3*y+z/3=100 AND x+y+z=100 THEN PRINT “鸡翁、母、雏的个数分别为：”；x、y、z END IF z=z+3‎ WEND ‎ y=y+1‎ ‎ z=3‎ WEND ‎ x=x+1‎ ‎ y=1‎ WEND END ‎3、设物共m个，被3，5，7除所得的商分别为x、y、z，则这个问题相当于求不定方程 ‎ 的正整数解.‎ m应同时满足下列三个条件：（1）m MOD 3=2；（2）m MOD 5=3；‎ ‎（3）m MOD 7=2.因此，可以让m从2开始检验，若3个条件中有任何一个不成立，则m递增1，一直到m同时满足三个条件为止.‎ 程序：m=2‎ f=0‎ WHILE f=0‎ IF m MOD 3=2 AND m MOD 5=3‎ AND m MOD 7=2 THEN PRINT “物体的个数为：”；m f=1‎ ELSE m=m+1‎ END IF WEND END ‎4、先把函数整理成 f（x）=（（（（0.00833x+0.04167）x+0.16667）x+0.5）x+1）x+1，按照从内向外的顺序依次进行. ‎ x=－0.2‎ a5=0.00833 V0=a5=0.008333‎ a4=0.04167 V1=V0x+a4=0.04‎ a3=0.016667 V2=V1x+a3=0.15867‎ a2=0.5 V3=V2x+a2=0.46827 ‎ a1=1 V4=V3x+a1=0.90635‎ a0=1 V5=V4x+a0=0.81873‎ ‎∴f（－0.2）=0.81873.‎ ‎5、每一趟都从头开始，两个两个地比较，若前者小，则两数位置不变；否则，调整这两个数的位置.‎ 解：第一趟的结果是：‎ ‎6 3 8 18 21 54 67‎ 完成3次交换.‎ 第二趟的结果是：‎ ‎3 6 8 18 21 54 67‎ 完成1次交换.‎ 第三趟交换次数为0，说明已排好次序，‎ 即3 6 8 18 21 54 67.‎ ‎6、解：（1）101111011（2）=1×28+0×27+1×26+1×25+1×24+1×23+0×22+1×21+1=379.‎ ‎（2）53（8）=5×81+3=43.‎ ‎∴53（8）=101011（2）.‎