- 2021-06-22 发布 |
- 37.5 KB |
- 2页

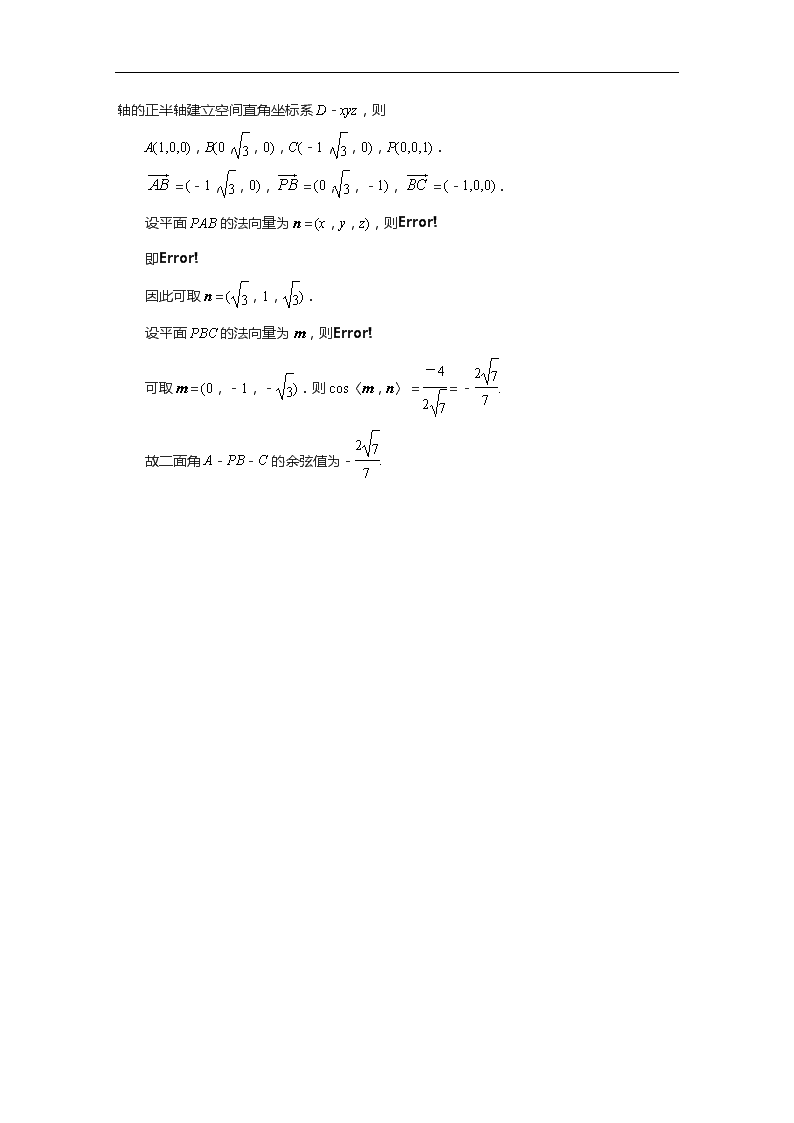
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2016届高考数学(理)5年高考真题备考试题库:第7章 第5节 直线、平面垂直的判定与性质
2010~2014年高考真题备选题库 第7章 立体几何 第5节 直线、平面垂直的判定与性质 1.(2012安徽,5分)设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 解析:若α⊥β,又α∩β=m,b⊂β,b⊥m,根据两个平面垂直的性质定理可得b⊥α,又因为a⊂α,所以a⊥b;反过来,当a∥m时,因为b⊥m,一定有b⊥a,但不能保证b⊥α,即不能推出α⊥β. 答案:A 2.(2011浙江,5分)下列命题中错误的是( ) A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β 解析:对于D,若平面α⊥平面β,则平面α内的直线可能不垂直于平面β,甚至可能平行于平面β,其余选项均是正确的. 答案:D 3.(2011新课标全国,12分)如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD. (1)证明:PA⊥BD; (2)若PD=AD,求二面角A-PB-C的余弦值. 解:(1)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD=AD. 从而BD2+AD2=AB2,故BD⊥AD. 又PD⊥底面ABCD,可得BD⊥PD. 所以BD⊥平面PAD.故PA⊥BD. (2)如图,以D为坐标原点,AD的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D-xyz,则 A(1,0,0),B(0,,0),C(-1,,0),P(0,0,1). =(-1,,0),=(0,,-1),=(-1,0,0). 设平面PAB的法向量为n=(x,y,z),则 即 因此可取n=(,1,). 设平面PBC的法向量为m,则 可取m=(0,-1,-).则cos〈m,n〉==-. 故二面角A-PB-C的余弦值为-.查看更多