吉林省北大附属长春实验学校2019届高三上学期第三次月考数学（理）试题

吉林省北大附属长春实验学校2019届高三上学期第三次月考数学（理）试题

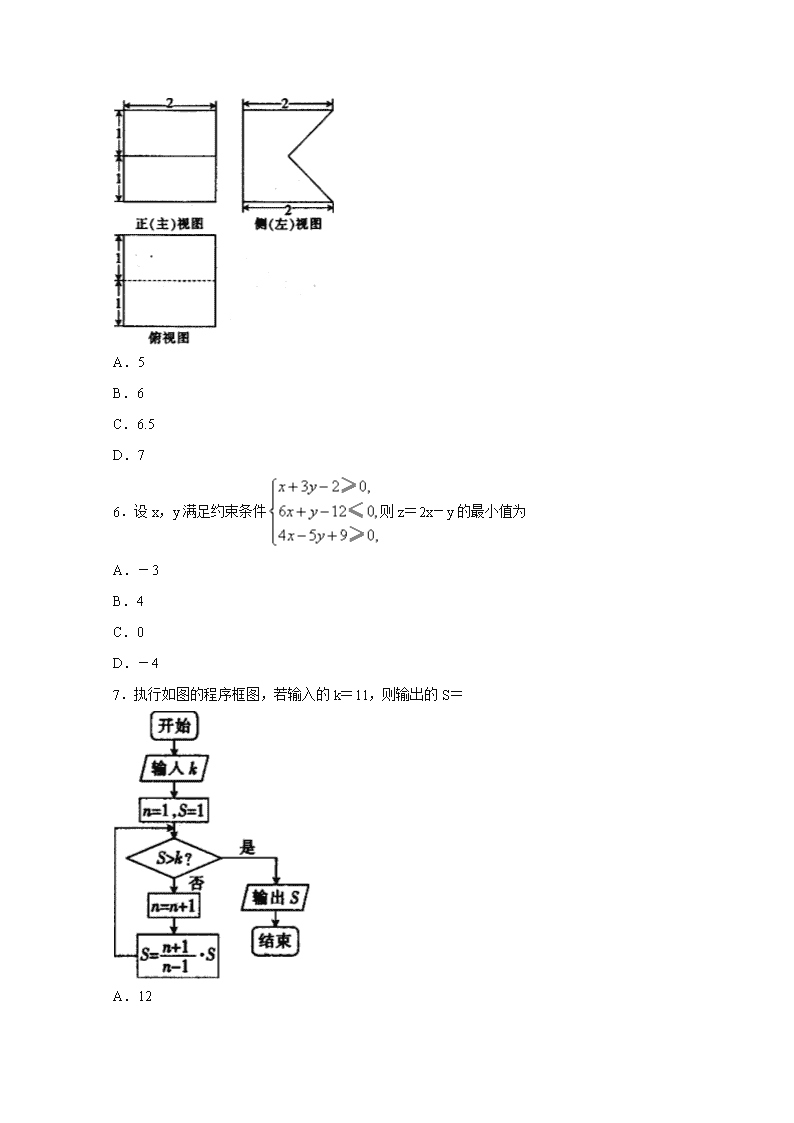
高三数学试卷（理科）‎ 第Ⅰ卷 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．设集合，B＝{x|x＞－2}，则 A．（－2，－1）‎ B．（－2，－1]‎ C．（－4，＋∞）‎ D．[－4，＋∞）‎ ‎2．设复数z＝1＋2i，则 A．z2＝2z－3‎ B．z2＝2z－4‎ C．z2＝2z－5‎ D．z2＝2z－6‎ ‎3．若双曲线的一个焦点为（－3，0），则m＝ ‎ A．‎ B．8‎ C．9‎ D．64‎ ‎4．设向量a、b满足|a|＝1，，且a·b＝1，则|a－2b|＝‎ A．2 ‎ B．‎ C．4‎ D．5‎ ‎5．某几何体的三视图如图所示，则该几何体的体积为 A．5‎ B．6‎ C．6.5‎ D．7‎ ‎6．设x，y满足约束条件则z＝2x－y的最小值为 A．－3‎ B．4‎ C．0‎ D．－4‎ ‎7．执行如图的程序框图，若输入的k＝11，则输出的S＝‎ A．12‎ B．13‎ C．15‎ D．18‎ ‎8．若函数f（x）＝|2x－4|－a存在两个零点，且一个为正数，另一个为负数，则a的取值范围为 A．（0，4）‎ B．（0，＋∞）‎ C．（3，4）‎ D．（3，＋∞）‎ ‎9．已知等差数列{an}的前n项和为Sn，a2＝1，则“a3＞5”是“S3＋S9＞93”的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎10．函数，f（x）＝Acos（wx＋φ）（A＞0，w＞0，－π＜φ＜0）的部分图象如图所示，为了得到g（x）＝Asinwx的图象，只需将函数y＝f（x）的图象 A．向左平移个单位长度 B．向右平移个单位长度 C．向右平移个单位长度 D．向左平移个单位长度 ‎11．在四面体ABCD中，AD⊥底面ABC，‎ ‎，BC＝2，E为棱BC的中点，点G在AE上且满足AG＝2GE，若四面体ABCD的外接球的表面积为，则tan∠AGD＝‎ A．‎ B．2‎ C．‎ D．‎ ‎12．已知函数f（x）的导数为f′（x），f（x）不是常数函数，且（x＋1）f（x）＋xf′（x）≥0对x∈[0，＋∞）恒成立，则下列不等式一定成立的是 A．f（1）＜2ef（2）‎ B．ef（1）＜f（2）‎ C．f（1）＜0‎ D．ef（e）＜2f（2）‎ 第Ⅱ卷 二、填空题 ‎13．若函数f（x）＝log8x＋log2x2，则，f（8）＝________．‎ ‎14．在（x＋a）9的展开式中，若第四项的系数为84，则a＝________．‎ ‎15．直线l经过抛物线y2＝4x的焦点F，且与抛物线交于A，B两点，若，则直线l的斜率为________．‎ ‎16．在数列{an}中，a1＝12，且．记，，则下列判断正确的是________．（填写所有正确结论的编号）‎ ‎①数列为等比数列；②存在正整数n，使得an能被11整除；‎ ‎③S10＞T243；④T21能被51整除．‎ 三、解答题 ‎17．在△ABC中，角A，B，C所对的边分别为a，b，c，且．‎ ‎（1）求角C；‎ ‎（2）若，△ABC的面积为，D为AB的中点，求sin∠BCD．‎ ‎18．某家电公司根据销售区域将销售员分成A，B两组．2017年年初，公司根据销售员的销售业绩分发年终奖，销售员的销售额（单位：十万元）在区间[90，95），[95，100），[100，105），[105，110]内对应的年终奖分别为2万元，2.5万元，3万元，3.5万元．已知200名销售员的年销售额都在区间[90，110]内，将这些数据分成4组：[90，95），[95，100），[100，105），[105，110]，得到如下两个频率分布直方图：‎ 以上面数据的频率作为概率，分别从A组与B组的销售员中随机选取1位，记X，Y分别表示A组与B组被选取的销售员获得的年终奖．‎ ‎（1）求X的分布列及数学期望；‎ ‎（2）试问A组与B组哪个组销售员获得的年终奖的平均值更高？为什么？‎ ‎19．如图，在四棱锥P－ABCD中，AC⊥BD，AC∩BD＝O，PO⊥AB，△POD是以PD为斜边的等腰直角三角形，且．‎ ‎（1）证明：平面PAC⊥平面PBD；‎ ‎（2）求二面角A－PD－B的余弦值．‎ ‎20．已知椭圆（a＞b＞0）的焦距与椭圆的短轴长相等，且W与Ω长轴长相等，这两个椭圆在第一象限的交点为A，直线l与直线OA（O为坐标原点）垂直，且l与W交于M，N两点．‎ ‎（1）求W的方程；‎ ‎（2）求△MON的面积的最大值．‎ ‎21．已知a∈R，函数．‎ ‎（1）若曲线y＝f（x）在点（0，f（0））处的切线的斜率为，判断函数，f（x）在上的单调性；‎ ‎（2）若，证明：f（x）＞2a对x∈R恒成立．‎ ‎22．[选修4—4：坐标系与参数方程]‎ 在直角坐标系xOy中，曲线C1的参数方程为（α为参数），直线C2的方程为，以O为极点，x轴的正半轴为极轴建立极坐标系．‎ ‎（1）求曲线C1和直线C2的极坐标方程；‎ ‎（2）若直线C2与曲线C1交于A，B两点，求．‎ ‎23．[选修4—5：不等式选讲]‎ 已知函数f（x）＝|x|＋|x－3|．‎ ‎（1）求不等式的解集；‎ ‎（2）若k＞0，且直线y＝kx＋5k与函数f（x）的图象可以围成一个三角形，求k的取值范围．‎ ‎高三数学试卷参考答案（理科）‎ ‎1．D ‎2．C ‎3．B ‎4．B ‎5．B ‎6．A ‎7．C ‎8．C ‎9．A ‎10．D ‎11．B ‎12．A ‎13．7‎ ‎14．1‎ ‎15．‎ ‎16．①②④‎ ‎17．解：（1）由，得，由正弦定理可得，‎ ‎，因为sinB≠0，所以，因为0＜C＜π，‎ 所以．‎ ‎（2）因为，故△ABC为等腰三角形，且顶角，‎ 故，‎ 所以a＝2，在△DBC中，由余弦定理可得，CD2＝DB2＋BC2－2DB·BCcosB＝7，‎ 所以，在△DBC中，由正弦定理可得，，‎ 即，所以．‎ ‎18．解：（1）A组销售员的销售额在[90，95），[95，100），[100，105），[105，110]的频率分别为：0．2，0．3，0．2，0．3，‎ 则X的分布列为：‎ X（元）‎ ‎20000‎ ‎25000‎ ‎30000‎ ‎35000‎ P ‎0.2‎ ‎0.3‎ ‎0.2‎ ‎0.2‎ 故E（X）＝20000×0.2＋25000×0.3＋30000×0.2＋35000×0.3＝28000（元）．‎ ‎（2）B组销售员的销售额在 [90，95），[95，100），[100，105），[105，110]的频率分别为：0．1，0．35，0．35，0．2，‎ 则Y的分布列为：‎ X（元）‎ ‎20000‎ ‎25000‎ ‎30000‎ ‎35000‎ P ‎0.1‎ ‎0.35‎ ‎0.35‎ ‎0.2‎ 故E（Y）＝20000×0.1＋25000×0.35＋30000×0.35＋35000×0.2＝28250（元）．‎ ‎∵E（X）＜E（Y），‎ ‎∴B组销售员获得的年终奖的平均值更高．‎ ‎19．（1）证明：∵△POD是以PD为斜边的等腰直角三角形，‎ ‎∴PO⊥DO．‎ 又PO⊥AB，AB∩DO＝B，∴PO⊥平面ABCD，‎ 则PO⊥AC，又AC⊥BD，BD∩PO＝O，‎ ‎∴AC⊥平面PBD．‎ 又AC平面PAC，∴平面PAC⊥平面PBD．‎ ‎（2）解：以O为坐标原点，建立如图所示的空间直角坐标系O－xyz，‎ 则A（3，0，0），D（0，－2，0），P（0，0，2），‎ 则，，‎ 设n＝（x，y，z）是平面ADP的法向量，‎ 则，即，‎ 令y＝3得n＝（2，3，－3）．‎ 由（1）知，平面PBD的一个法向量为，‎ ‎∴，‎ 由图可知，二面角A－PD－B的平面角为锐角，‎ 故二面角A－PD－B的平面角的余弦值为．‎ ‎20．解：（1）由题意可得，∴，‎ 故W的方程为．‎ ‎（2）联立，得，‎ ‎∴，又A在第一象限，∴．‎ 故可设l的方程为y＝3x＋m．‎ 联立，得31x2－18mx＋3m2－12＝0，‎ 设M（x1，y1），N（x2，y2），则，，‎ ‎∴，‎ 又O到直线l的距离为，则△MON的面积，‎ ‎∴，‎ 当且仅当m2＝31－m2，即，满足Δ＞0，故△MON的面积的最大值为．‎ ‎21．（1）解：∵，‎ ‎∴，‎ ‎∴，∴ａ＝0．‎ ‎∴，‎ 当时，2x＋1＞0，e2x＞0，ex＞0，∴f′（x）＞0，‎ ‎∴函数f（x）在上单调递增．‎ ‎（2）证明：设，g′（x）＝（x＋1）ex，‎ 令g′（x）＞0，得x＞－1，g（x）递增；令g′（x）＜0，得x＜－1，g（x）递减．‎ ‎∴，∵e≈2.7，∴，∴g（x）＞1．‎ 设h（x）＝ex－ax，令h′（x）＝0得x＝lna，‎ 令h′（x）＞0，得x＞lna，h（x）递增；令h′（x）＜0，得x＜lna，h（x）递减．‎ ‎∴h（x）min＝h（lna）＝a－alna＝a（1－lna），‎ ‎∵，∴lna＜－1，∴1－lna＞2，∴h（x）min＞2a，∴h（x）＞2a＞0．‎ 又g（x）＞1，∴g（x）h（x）＞2a，即f（x）＞2a．‎ ‎22．解：（1）曲线C1的普通方程为（x－2）2＋（y－2）2＝1，则C1的极坐标方程为ρ2－4ρcosθ－4ρsinθ＋7＝0，由于直线C2过原点，且倾斜角为，故其极坐标为（ρ∈R）（或）．‎ ‎（2）由得，‎ 故，，‎ ‎∴．‎ ‎23．解：（1）由即得，‎ 或或，‎ 解得－3＜x＜9，∴不等式的解集为（－3，9）．‎ ‎（2）作出函数的图象，如图所示，‎ ‎∵直线y＝k（x＋5）经过定点A（－5，0），‎ ‎∴当直线y＝k（x＋5）经过点B（0，3）时，，‎ ‎∴当直线y＝k（x＋5）经过点C（3，3）时，．‎ ‎∴当时，直线y＝kx＋5k与函数f（x）的图象可以围成一个三角形．‎