专题7-3+二元一次不等式（组）与线性规划（练）-2018年高考数学（文）一轮复习讲练测

专题7-3+二元一次不等式（组）与线性规划（练）-2018年高考数学（文）一轮复习讲练测

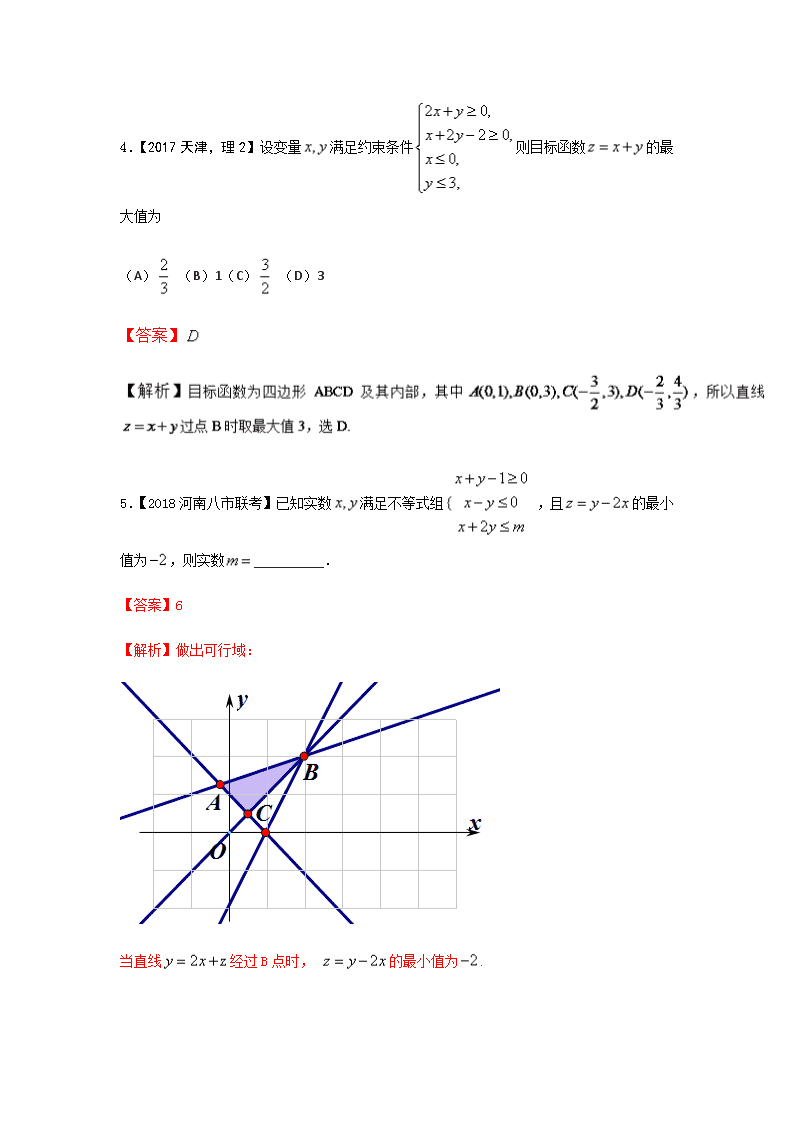
全品教学网2018年高考数学讲练测【新课标版文】【练】【来.源：全,品…中&高*考*网】第七章 不等式 第03节 二元一次不等式（组）与线性规划 A基础巩固训练 ‎1．若关于x，y的不等式组‎{‎x≤0‎x+y≥0‎kx-y+1≥0‎，表示的平面区域是等腰直角三角形区域，则其表示的区域面积为（ ）‎ A. 1或 B. 或 C. 1或 D. 或 ‎【答案】B ‎【解析】x+y=0的斜率为-1，x=0倾斜角为‎90‎‎0‎，而直线kx-y+1=0的过定点(0,1),当k=0时，满足条件，面积为。当k=1时，满足条件，面积为。选B.‎ ‎2．【2018河南商丘模拟】不等式组所表示的平面区域为，若直线与有公共点，则实数的最小值为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】【来.源：全,品…中&高*考*网】‎ 由得:y-1=a(x+1),故直线恒过(-1,1),由图象得,直线AB的斜率为: ,故选B.‎ ‎3．【2018百校联盟联考】若函数的图像上存在点，满足约束条件，则实数的最大值为__________．‎ ‎【答案】1‎ ‎【解析】【来.源：全,品…中&高*考*网】‎ 作出不等式组表示的平面区域，得到如图的三角形，再作出对数函数的图象，可得该图象与直线交于点，当该点在区域内时，图象上存在点满足不等式组，即符合题意，即的最大值为1，故答案为1. ‎ ‎4．【2017天津，理2】设变量满足约束条件则目标函数的最大值为 ‎（A） （B）1（C） （D）3‎ ‎【答案】 【来.源：全,品…中&高*考*网】‎ ‎5．【2018河南八市联考】已知实数满足不等式组，且的最小值为，则实数__________．‎ ‎【答案】6‎ ‎【解析】做出可行域：‎ 当直线经过B点时， 的最小值为.‎ 此时，即，即 B能力提升训练 ‎1．【2017安徽阜阳二模】不等式所对应的平面区域的面积为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】不等式所对应的平面区域为一个菱形及其内部，对角线长分别为，所以面积为 选B.‎ ‎2. 【2017湖南娄底二模】记不等式组所表示的平面区域为，若对任意，不等式恒成立，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】根据平面区域，易知当时，由题设得，所以，故选D.‎ ‎3．已知变量x，y满足则的取值范围是( )‎ A． B． C． D．‎ ‎【答案】A ‎4．【2018云南玉溪第一中学模拟】已知变量满足约束条件，目标函数的最小值为，则实数____________.‎ ‎【答案】‎ ‎【解析】约束条件对应的可行域为三角形区域，‎ 其中顶点，由得,经过点 时取得最小值-5，即.‎ ‎5．【2017福建三明5月质检】在区域中，若满足的区域面积占面积的，则实数的值是（　）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】如图所示，绘制不等式所表示的可行域， ，‎ 则满足的区域面积，据此可得： ，‎ 代入直线方程可得： .‎ 本题选择C选项.‎ ‎6．【2018江西赣州红色七校联考】设实数满足 x+y-3≤0‎y-‎1‎‎2‎x≥0‎x-1≥0‎ , 则 u=yx-‎xy 的取值范围为（ ）‎ A. ‎[‎1‎‎2‎,2]‎ B. ‎[-‎2‎‎3‎,2]‎ C. ‎[-‎2‎‎3‎,‎3‎‎2‎]‎ D. ‎[-‎3‎‎2‎,‎3‎‎2‎]‎【来.源：全,品…中&高*考*网】‎ ‎【答案】D ‎【解析】画出可行域如图所示：‎ u=yx-‎xy‎，设k=‎yx表示可行域中的点与点(0,0)连线的斜率，‎ 由图知k∈‎‎1‎‎2‎‎,2‎，‎ ‎∴利用函数u=k-‎‎1‎k单调递增可得u的取值范围为‎[-‎3‎‎2‎,‎3‎‎2‎]‎ .‎ 本题选择D选项.‎ ‎ C 思维拓展训练 ‎1．【2018贵州贵阳联考】已知实数满足，直线 过定点，则的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎2．已知不等式组，表示的平面区域为D，点．若点M是D上的动点，则的最小值是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】‎ ‎3．已知实数满足，则的最大值是（ ）‎ A. B. C . D. ‎ ‎【答案】D ‎【解析】根据约束条件可作出如下可行域，‎ 将目标函数，转化为，在可行域中画出抛物线的大致图像，可知经过点时，取到最大值，此时，故选D.‎ ‎4．【2018河北邯郸模拟】已知函数，点是平面区域内的任意一点，若的最小值为-6，则的值为（ ）‎ A. -1 B. 0 C. 1 D. 2‎ ‎【答案】A ‎【解析】由函数的解析式可得： ，‎ 结合题意可得目标函数在给定的可行域内的最小值为，‎ 可行域的顶点坐标为，‎ 结合目标函数的几何意义可得目标函数在点处取得最小值，‎ 即： ，解得： .‎ 本题选择A选项. ‎ ‎5．已知点在内（不含边界），且，则的取值范围为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【来.源：全,品…中&高*考*网】‎ ‎ ‎