- 2021-06-22 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
云南省玉溪一中10-11学年高二数学下学期期末考试 文 新人教A版
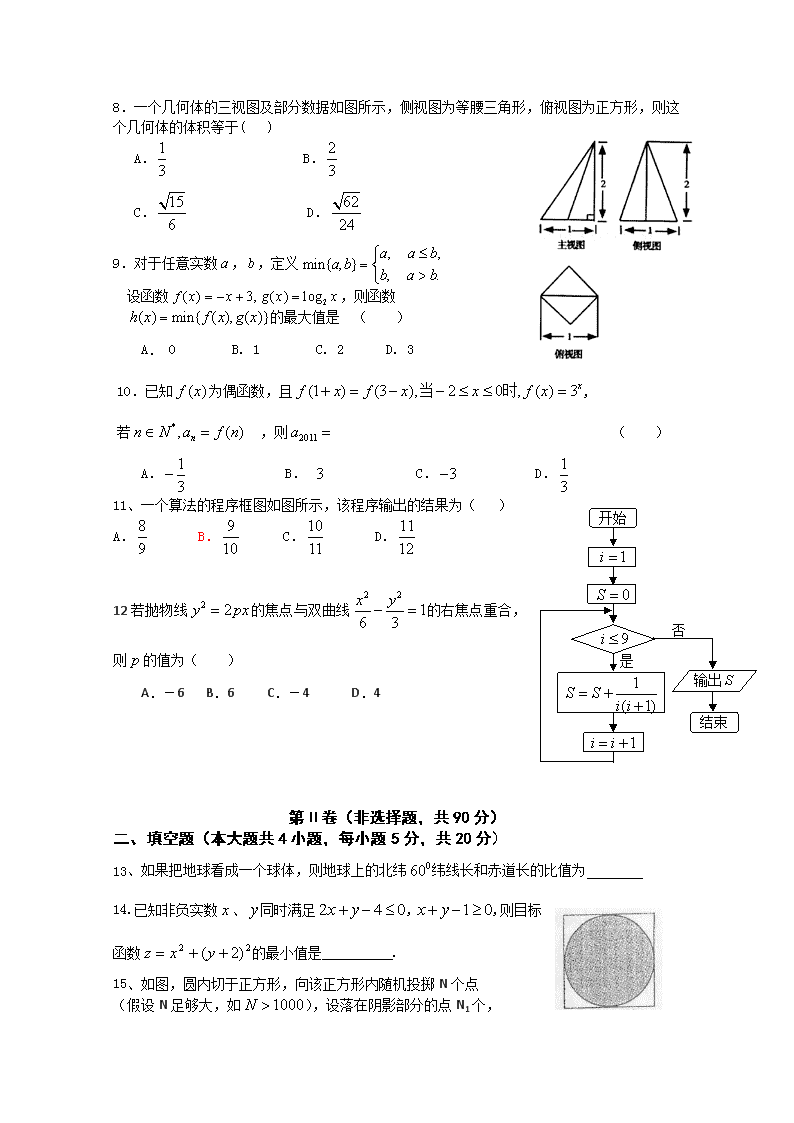
玉溪一中2012届高二下学期期末测试文 科 数 学 试 卷 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟,答案均填写在答题卡上,否则无效。 参考公式: 球的表面积公式 : ,球的体积公式 : 其中R表示球的半径 柱体的体积公式 :v=sh 锥体的体积公式 :v=sh 第Ⅰ卷(选择题,共60分) 一、选择题(本大题共12小题,每小题5分,共60分) 1. 已知集合则为 ( ) A. B. C. D. 2.在中,“”是“为锐角三角形”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既非充分又非必要条件 3.已知命题p:;命题q:,则下列命题为真命题的是( ) A. p∧q B. p∨(﹁q) C. (﹁p)∧q D. p∧(﹁q) 4.复数的共轭复数是( ) A. B. C. D. 5.已知直线被圆所截得的弦长为4,则是( ) A.-1 B.-2 C. 0 D.2 6.曲线的最小值为 ( ) A. B. C. D. 7. 一个单位有职工800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( ) A.12,24,15,9 B.9,12,12,7 C.8,15,12,5 D.8,16,10,6 8.一个几何体的三视图及部分数据如图所示,侧视图为等腰三角形,俯视图为正方形,则这个几何体的体积等于( ) A. B. C. D. 9.对于任意实数,,定义 设函数,则函数 的最大值是 ( ) A. 0 B. 1 C. 2 D. 3 10.已知为偶函数,且, 若 ,则 ( ) A. B. C. D. 结束 输出 开始 是 否 11、一个算法的程序框图如图所示,该程序输出的结果为( ) A. B. C. D. 12若抛物线的焦点与双曲线的右焦点重合,则的值为( ) A.-6 B.6 C.-4 D.4 第Ⅱ卷(非选择题,共90分) 二、填空题(本大题共4小题,每小题5分,共20分) 13、如果把地球看成一个球体,则地球上的北纬纬线长和赤道长的比值为 14. 已知非负实数、同时满足,, 则目标函数的最小值是 . 15、如图,圆内切于正方形,向该正方形内随机投掷N个点 (假设N足够大,如),设落在阴影部分的点N1个, 那么由随机模拟思想可得圆周率的近似值为 。 16、设P是一个数集,且至少含有两个数,若对任意a、b∈P,都有a+b、a-b、ab、∈P(除数b≠0)则称P是一个数域,例如有理数集Q是数域,有下列命题: ①数域必含有0,1两个数; ②整数集是数域; ③若有理数集QM,则数集M必为数域; ④数域必为无限集. 其中正确的命题的序号是 .(把你认为正确的命题的序号都填上) 三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤) 17、(本小题满分10分) 已知函数.求的单调区间; 18、(本小题满分12分已知等差数列{}中,求{}前n项和 19、(本小题满分12分) 在ABC中,C-A=, sinB=。 (I)求sinA的值; (II)设AC=,求△ABC的面积。 20.(本小题满分12分) 某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表: 甲厂: 分组 频数 12 63 86 182 92 61 4 乙厂: 分组 频数 29 71 85 159 76 62 18 (1) 试分别估计两个分厂生产的零件的优质品率; (2) 由以上统计数据填入答题卡的列联表,并问是否有99%的把握认为“ 两个分厂生产的零件的质量有差异”。 附: , K2=。 图5 直观图 俯视图 21. (本小题满分12分) 如图,四棱锥,≌, 在它的俯视图中,, ,. ⑴求证:是直角三角形; ⑵求四棱锥的体积. 22.(本小题满分12分))已知椭圆C过点,两个焦点为,,O为坐标原点。 (I)求椭圆C的方程; (2)直线l过 点A(—1,0),且与椭圆C交于P,Q两点,求△BPQ面积的最大值。 玉溪一中2012届高二下学期期末测试 文科数学 参考答案 一、选择题:CBCBA DDABD BB 二、填空题: 13、1:2 14. 5 15. (16)①④ 三、解答题: 17.解:由已知得.因为, 所以当. 故区间为的单调递减区间, 区间为的单调递增区间. 18. 解:设的公差为,则 即解得 因此 19.解:(1)∵∴ ∴ ∴ 又 ∴ (2)由正弦定理得∴ ∴ 20.解:(Ⅰ)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为; 乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为 (Ⅱ) 甲厂 乙厂 合计 优质品 360 320 680 非优质品 140 180 320 合计 500 500 1000 所以有99%的把握认为“两个分厂生产的零件的质量有差异”。 21.解:.解:⑴由已知,点在底面上的投影是点,所以 因为、,所以, 因为≌,所以, 因为,所以平面, 所以,是直角三角形 ⑵连接,因为,,所以是等边三角形 在中,根据多边形内角和定理计算得 又因为,所以 所以,, 所以 又, 所以,四棱锥的体积 22.解:(Ⅰ)由题意,,可设椭圆方程为。 因为A在椭圆上,所以,解得,(舍去) 所以椭圆方程为 设直线为:,,,则 所以 令,则,所以,而在上单调递增 所以。 当时取等号,即当时,的面积最大值为3。 查看更多