2018-2019学年山西省范亭中学高二上学期期中考试数学（文）试题（Word版）

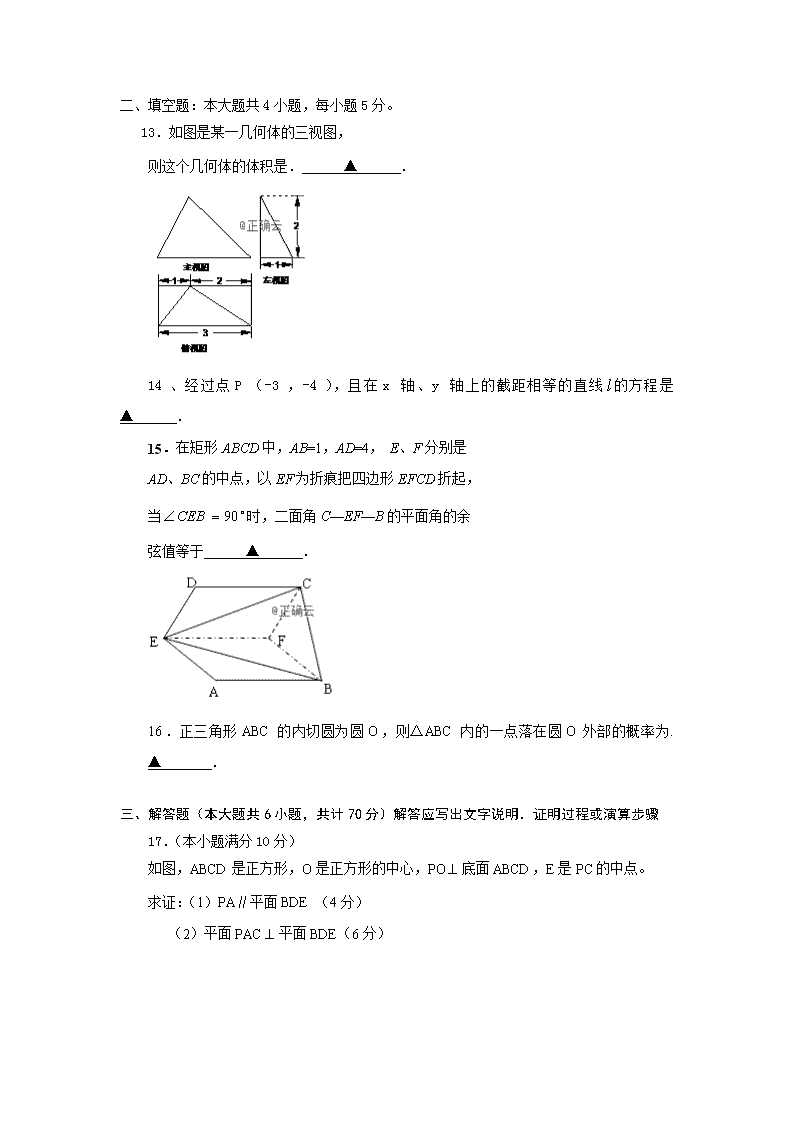
2018-2019学年山西省范亭中学高二上学期期中考试数学（文）试题（Word版）

范亭中学高二数学第一学期期中考试试题 高二文科数学 命题人： 丁垒柱 史晓娟 本试题分第I卷（选择题）和第II卷（非选择题）两部分，满分150分，‎ 考试时间120分钟 第I卷（选择题）‎ 一 选择题（本题共12道小题，每小题5分，共60分）‎ ‎1.设，，则=（ ）‎ A. B. ‎ C. D. ‎ ‎2、直线的倾斜角是（ ）‎ A．30°　　　　B．60° C．120° D.135°‎ ‎3、下列函数中，定义域与值域相同的是 A. B. C. D.‎ ‎4. 一个平面内有无数条直线平行于另一个平面，那么这两个平面 A、 一定平行 B、一定相交 C、平行或相交 D、一定重合 ‎5. 两圆和的位置关系是 Ａ、相离　　　　Ｂ、相交　　　Ｃ、内切　　　　Ｄ、外切 ‎6、在空间直角坐标系中，点关于原点的对称点坐标是（ ）‎ A．B．C．D．‎ ‎7、如图：直线L1 的倾斜角1=30０，直线L1L2 ，则L2的斜率为 ‎（　　）‎ Ａ、　　Ｂ、　　　　Ｃ、　　　Ｄ、‎ ‎8、若a，b是异面直线，直线c∥a，则c与b的位置关系是（ ）‎ A 、 相交 B、 异面 C、 平行 D、异面或相交 ‎9、已知向量＝(cos120°，sin120°)，＝(cos30°，sin30°)，则△ABC的形状为 A．直角三角形 B．钝角三角形 C．锐角三角形 D．等边三角形 ‎10. 直线与圆交于Ｅ、F两点，则EOF（O为原点）的面积为（ ）‎ A、 B、 C、 D、 ‎ ‎11．已知{an}是首项为1的等比数列，且4a1，2a2，a3成等差数列，则数列{an}的前5项的和为 A． B． C．32 D．31‎ ‎12.在圆内，过点的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为为（ ）‎ ‎（A） （B）‎ ‎（C） （D）‎ 第II卷（非选择题）‎ 二、填空题：本大题共4小题，每小题5分。‎ ‎13．如图是某一几何体的三视图，‎ 则这个几何体的体积是． ▲ ．‎ ‎14、经过点P（-3，-4），且在x轴、y轴上的截距相等的直线的方程是 ▲ ．‎ ‎15．在矩形ABCD中，AB=1，AD=4， E、F分别是 AD、BC的中点，以EF为折痕把四边形EFCD折起，‎ 当时，二面角C—EF—B的平面角的余 弦值等于 ▲ ．‎ ‎16．正三角形ABC的内切圆为圆O，则△ABC内的一点落在圆O外部的概率为. ▲ ．‎ 三、解答题（本大题共6小题，共计70分）解答应写出文字说明．证明过程或演算步骤 ‎17．（本小题满分10分）‎ 如图，ABCD是正方形，O是正方形的中心，PO底面ABCD，E是PC的中点。‎ ‎ 求证：（1）PA∥平面BDE （4分）‎ ‎（2）平面PAC平面BDE（6分）‎ ‎18、（本小题满分12分）‎ 已知圆c：(x-3)2+(y-4)2=4和直线：kx-y-4k+3=0.‎ ‎（1）求证：不论k取何值，直线和圆相交；‎ ‎（2）求k取何值时，圆被直线截得的弦最短，并求最短弦的长.‎ ‎19．（本小题满分12分）‎ 已知函数在定义域上为增函数，且满足，.‎ ‎（1）求、的值；‎ ‎（2）解不等式.‎ ‎20.(本小题满分12分)‎ 已知一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱。‎ ‎（1）求圆柱的侧面积 ‎（2）当x为何值时，圆柱的侧面积最大？‎ 21． ‎（本小题满分12分）‎ 如图，在棱长为a的正方体ABCD—A1B1C1D1中，E、F分别是棱AB与BC的中点．‎ ‎（1）求异面直线B1E与CC1间的距离；‎ ‎（2）求二面角B—FB1—E的大小；‎ ‎（3）求点D到平面B1EF的距离．‎ 22. ‎（本小题满分12分）‎ 已知直线l过点P（1，1），并与直线l1：x－y+3=0和 l2：2x+y－6=0分别交于点A、B，若线段AB被点P平分，求：‎ ‎（Ⅰ）直线l的方程 ‎（Ⅱ）以坐标原点O为圆心且被l截得的弦长为的圆的方程．‎ 答案 一、选择题 ACDC C DCDAD DA 二、填空题 ‎13. ２ ‎ ‎ ‎ ‎16． ‎ ‎17、证明（１）∵O是AC的中点，E是PC的中点，∴OE∥AP，………2‎ 又∵OE平面BDE，PA平面BDE，∴PA∥平面BDE ………3‎ 21． ‎∵PO底面ABCD，∴POBD，………1‎ 又∵ACBD，且ACPO=O………2‎ ‎∴BD平面PAC，而BD平面BDE，‎ ‎∴平面PAC平面BDE。………2‎ 22. ‎（1）证明：直线方程可化为y-3=k(x-4),知直线恒过点A（4，3），………2‎ 可证点（4，3）在圆内， ………2‎ 故结论可证。 ………1‎ ‎（2）解：作AC⊥，则⊥AC的弦最短，………3‎ 此时k=1，最短弦的长为 ………3‎ ‎19(1)‎ ‎(2)‎ 由题意得 ‎20、解（1）画圆锥及内接圆柱的轴截面如图 设：所求的圆柱的底面半径为r，它的侧面积为S，圆柱侧面积=2rx………1‎ ‎ ………3‎ ‎ ………2‎ ‎（2）‎ ‎………2‎ ‎ ‎ ‎ ………3‎ 即当圆柱的高是已知圆锥的高的一半时，它的侧面积最大………1‎ ‎21、（1）∵B1C1⊥平面A1B1BA B1C1⊥B1E 又B1C1⊥C1C ‎∴B1C1为异面直线B1E与CC1的公垂线段……………（3分）‎ 故B1E与CC1的距离为a…………………（4分）‎ ‎（2）作BH⊥B1F于H，连结EH ‎∵EB⊥平面B1BF ‎∴BH为EH在平面B1BF内的射影 ‎∴EH⊥B1F（三垂线定理）‎ ‎∴∠EHB为所求二面角的平面角………………………（6分）‎ ‎∵BH= ‎ ‎…………………（7分）‎ ‎∴二面角正切值为…………………（8分）‎ ‎（3）连结B1D1、BD，设BDEF=G，连结B1G ‎∵B1B⊥平面ABCD ∴B1B⊥EF 又EF⊥BD且B1BBD=B ‎∴EF⊥平面D1DBB1 ∴平面B1EF⊥平面D1DBB1‎ 作DQ⊥B1G的延长线于Q，则DQ⊥平面B1EF ∴DQ长即为所求…………（12分）‎ 又G为BD四等分点，∴B1G=DG ∴DQ=a即D到平面B1EF的距离为a…………（14分） ‎ ‎（也可用等体积法）‎ ‎22解：（Ⅰ）依题意可设A、，则 ‎ ， ，解得，． ………………4分 ‎ 即，又l过点P，易得AB方程为． ………………6分 ‎（Ⅱ）设圆的半径为R，则，其中d为弦心距，，可得，故所求圆的方程为．……………………12分