2017-2018学年贵州省遵义四中高二上学期第二次月考数学试题（文科）（解析版）

2017-2018学年贵州省遵义四中高二上学期第二次月考数学试题（文科）（解析版）

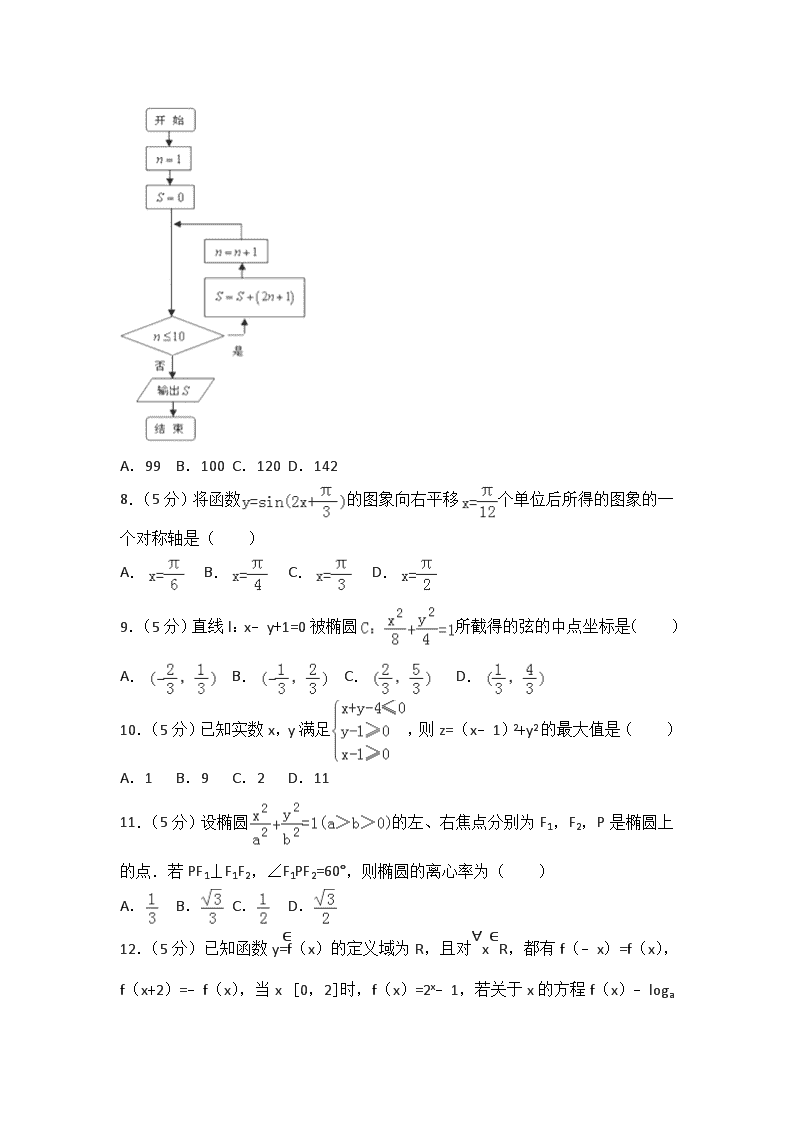
‎2017-2018学年贵州省遵义四中高二（上）第二次月考数学试卷（文科）‎ ‎　‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1．（5分）已知全集U={1，2，3，4，5}，集合A={1，2}，B={2，3，4}，则（∁UA）∩B=（　　）‎ A．{2} B．{3，4} C．ab＞0 D．a＞0‎ ‎2．（5分）等差数列{an}中，已知a4+a8=16，则a6=（　　）‎ A．6 B．10 C．8 D．4‎ ‎3．（5分）已知椭圆，焦点在y轴上，且焦距为4，则m=（　　）‎ A．10 B．12 C．8 D．36‎ ‎4．（5分）“x=1”是“x2﹣1=0”的（　　）‎ A．充分而不必要条件 B．必要而充分不条件 C．充要条件 D．既不充分也不必要条件 ‎5．（5分）下列命题中是假命题的是（　　）‎ A．∃x0∈R，lgx0=0 B．∃x0∈R，tanx0=1‎ C．∀x∈R，x2＞0 D．∀x∈R，2x＞0‎ ‎6．（5分）若两直线l1：x+my﹣1=0，l2：mx+y+4=0互相平行，则m=（　　）‎ A．﹣2 B．1 C．1或﹣1 D．﹣2或1‎ ‎7．（5分）执行如图所示程序框图所表达的算法，输出的结果是（　　）‎ A．99 B．100 C．120 D．142‎ ‎8．（5分）将函数的图象向右平移个单位后所得的图象的一个对称轴是（　　）‎ A． B． C． D．‎ ‎9．（5分）直线l：x﹣y+1=0被椭圆所截得的弦的中点坐标是（　　）‎ A． B． C． D．‎ ‎10．（5分）已知实数x，y满足，则z=（x﹣1）2+y2的最大值是（　　）‎ A．1 B．9 C．2 D．11‎ ‎11．（5分）设椭圆的左、右焦点分别为F1，F2，P是椭圆上的点．若PF1⊥F1F2，∠F1PF2=60°，则椭圆的离心率为（　　）‎ A． B． C． D．‎ ‎12．（5分）已知函数y=f（x）的定义域为R，且对∀x∈R，都有f（﹣x）=f（x），f（x+2）=﹣f（x），当x∈[0，2]时，f（x）=2x﹣1，若关于x的方程f（x）﹣loga ‎（x+2）=0（a＞1）在区间[﹣2，10]上有五个不同的根，则a的取值范围是（　　）‎ A．（1，2） B．（2，+∞） C． D．‎ ‎　‎ 二、填空题（本大题共20分，每小题5分）‎ ‎13．（5分）已知向量=　 　．‎ ‎14．（5分）已知函数f（x）=，则f（f（））　 　．‎ ‎15．（5分）已知椭圆+=1的焦点为F1，F2，P是椭圆上一点，△F1PF2的周长为　 　．‎ ‎16．（5分）设m，n∈R，若直线（m+1）x+（n+1）y﹣2=0与圆（x﹣1）2+（y﹣1）2=1相切，则m+n的取值范围是　 　．‎ ‎　‎ 三、解答题（解答应写出文字说明，证明过程或演算步骤．）‎ ‎17．（10分）在锐角三角形ABC中，内角A，B，C的对边分别为a，b，c且2asinB=b．‎ ‎（1）求角A的大小；‎ ‎（2）若a=6，b+c=8，求△ABC的面积．‎ ‎18．（12分）随机抽取100名学生，他们的身高（单位cm）的频率分布直方图如图所示．‎ ‎（1）求频率分布直方图中的x的值及身高在170cm以上的学生人数；‎ ‎（2）将身高在[170，175），[175，180），[180，185）区间内的学生依次记为A，B，C三组，用分层抽样的方法从这三组中抽取6人，求从这三组分别抽取的人数；‎ ‎（3）在（Ⅱ）的条件下从6名学生中抽取2人，计算B组中至少有1人被抽中的概率．‎ ‎19．（12分）已知数列{an}是等差数列，a2=6，a5=18，数列{bn}的前n项和为Tn．且Tn=2bn﹣2‎ ‎（1）求{an}，{bn}的通项公式；‎ ‎（2）令cn=anbn，求数列{cn}的前n项和Sn．‎ ‎20．（12分）如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的点．‎ ‎（1）证明：PB∥平面AEC；‎ ‎（2）设AP=1，AD=，三棱锥P﹣ABD的体积V=，求A点到平面PBD的距离．‎ ‎21．（12分）已知，圆C：x2+y2﹣8y+12=0，直线l：ax+y+2a=0．‎ ‎（1）当a为何值时，直线l与圆C相切；‎ ‎（2）当直线l与圆C相交于A、B两点，且AB=2时，求直线l的方程．‎ ‎22．（12分）已知椭圆C：的右焦点为，离心率为．‎ ‎（1）求椭圆的标准方程；‎ ‎（2）若直线l与椭圆相交于A，B两点，且以AB为直径的圆经过原点O，求证：点O到直线AB的距离为定值；‎ ‎（3）在（2）的条件下，求△OAB面积的最大值．‎ ‎　‎ ‎2017-2018学年贵州省遵义四中高二（上）第二次月考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1．（5分）已知全集U={1，2，3，4，5}，集合A={1，2}，B={2，3，4}，则（∁UA）∩B=（　　）‎ A．{2} B．{3，4} C．ab＞0 D．a＞0‎ ‎【分析】根据补集与交集的定义，计算即可．‎ ‎【解答】解：全集U={1，2，3，4，5}，集合A={1，2}，B={2，3，4}，‎ ‎∴∁UA={3，4，5}，‎ ‎∴（∁UA）∩B={3，4}．‎ 故选：B．‎ ‎【点评】本题考查了集合的定义与运算问题，是基础题．‎ ‎　‎ ‎2．（5分）等差数列{an}中，已知a4+a8=16，则a6=（　　）‎ A．6 B．10 C．8 D．4‎ ‎【分析】由等差数列中项的定义，2a6=a4+a8，计算即可得到所求值．‎ ‎【解答】解：等差数列{an}中，a4+a8=16，‎ 可得2a6=a4+a8=16，‎ 解得a6=8．‎ 故选C．‎ ‎【点评】本题考查等差数列中项的定义和计算，考查方程思想，属于基础题．‎ ‎　‎ ‎3．（5分）已知椭圆，焦点在y轴上，且焦距为4，则m=（　　）‎ A．10 B．12 C．8 D．36‎ ‎【分析】利用已知条件列出方程，求解即可．‎ ‎【解答】解：椭圆，焦点在y轴上，且焦距为4，c=2；‎ ‎∴m﹣2＞10﹣m＞0，可得c2=a2﹣b2，即m﹣2﹣（10﹣m）=4，‎ 解得m=8．‎ 故选：C．‎ ‎【点评】本题考查椭圆的简单性质的应用，考查计算能力．‎ ‎　‎ ‎4．（5分）“x=1”是“x2﹣1=0”的（　　）‎ A．充分而不必要条件 B．必要而充分不条件 C．充要条件 D．既不充分也不必要条件 ‎【分析】利用充分条件和必要条件的定义进行判断．‎ ‎【解答】解：由x2﹣1=0，解得x=±1，‎ ‎∴“x=1”是“x2﹣1=0”的充分不必要条件．‎ 故选A．‎ ‎【点评】本题主要考查充分条件和必要条件的判断和应用，比较基础．‎ ‎　‎ ‎5．（5分）下列命题中是假命题的是（　　）‎ A．∃x0∈R，lgx0=0 B．∃x0∈R，tanx0=1‎ C．∀x∈R，x2＞0 D．∀x∈R，2x＞0‎ ‎【分析】求出x0，判断A、B的正误；利用反例判断C的正误；指数函数的性质判断D的正误；‎ ‎【解答】解：当x0=1时，lgx0=0，所以∃x0∈R，lgx0=0，正确；‎ 当x0=时，tanx0=1，所以∃x0∈R，tanx0=1，正确；‎ 当x=0时，x2=0，所以∀x∈R，x2＞0不正确；‎ 由指数函数y=2x＞0，可知∀x∈R，2x＞0，正确；‎ 故选：C．‎ ‎【点评】本题考查命题的真假的判断，全称命题与特称命题的判断，指数函数的性质的应用，是基本知识的考查．‎ ‎　‎ ‎6．（5分）若两直线l1：x+my﹣1=0，l2：mx+y+4=0互相平行，则m=（　　）‎ A．﹣2 B．1 C．1或﹣1 D．﹣2或1‎ ‎【分析】由两直线平行的条件可得=≠，解方程即可得到所求值．‎ ‎【解答】解：两直线l1：x+my﹣1=0，l2：mx+y+4=0互相平行，‎ 当m=0时，两直线分别为x=1和y=﹣4显然垂直；‎ 可得=≠，‎ 解得m=±1．‎ 故选：C．‎ ‎【点评】本题考查两直线平行的条件，考查方程思想和运算能力，属于基础题．‎ ‎　‎ ‎7．（5分）执行如图所示程序框图所表达的算法，输出的结果是（　　）‎ A．99 B．100 C．120 D．142‎ ‎【分析】由图知，每次进入循环体后，新的s值是s加上2n+1得到的，故由此运算规律进行计算，经过10次运算后输出的结果即可．‎ ‎【解答】解：由图知s的运算规则是：s=s+（2n+1），故有：‎ 第一次进入循环体后s=3，n=2，‎ 第二次进入循环体后s=3+5，n=3，‎ 第三次进入循环体后s=3+5+7，n=4，‎ 第四次进入循环体后s=3+5+7+9，n=5，‎ ‎…‎ 第10次进入循环体后s=3+5+7+9+…+21，n=11．‎ 由于n=11＞10，退出循环．‎ 故该程序运行后输出的结果是：s=3+5+7+9+…+21=120．‎ 故选C．‎ ‎【点评】本题考查循环结构，已知运算规则与运算次数，求最后运算结果的一个题，是算法中一种常见的题型．‎ ‎　‎ ‎8．（5分）将函数的图象向右平移个单位后所得的图象的一个对称轴是（　　）‎ A． B． C． D．‎ ‎【分析】根据函数图象的平移，求出平移后得到的函数的解析式，依据对称轴的定义，令 2x+=kπ+，k∈z，‎ 解出 x=+，k∈z 为其对称轴方程．‎ ‎【解答】解：将函数的图象向右平移个单位后所得的函数的解析式为 ‎ y=sin[2（x﹣）+]=sin（2x+）．‎ 令 2x+=kπ+，k∈z，可得 x=+，k∈z．令k=0，可得 x=，‎ 故选 A．‎ ‎【点评】本题考查函数图象的平移，正弦函数的对称轴，凡过顶点且垂直于x轴的直线都是其对称轴．‎ ‎　‎ ‎9．（5分）直线l：x﹣y+1=0被椭圆所截得的弦的中点坐标是（　　）‎ A． B． C． D．‎ ‎【分析】将直线方程代入椭圆方程，利用韦达定理及中点坐标公式求得弦的中点横坐标，代入直线方程，即可求得弦的中点纵坐标，即可求得弦的中点坐标．‎ ‎【解答】解：设直线x﹣y+1=0与椭圆交于A（x1，y1），B（x2，y2），‎ 由，消去y整理得x2+2（x+1）2=8，‎ ‎∴3x2+4x﹣6=0，‎ 由韦达定理可知：x1+x2=﹣，‎ ‎∴弦的中点横坐标是x=﹣，‎ 代入直线方程中，得y=x+1=，‎ ‎∴弦的中点是（﹣，）‎ 故选：A．‎ ‎【点评】本题考查椭圆的标准方程，直线与椭圆的位置关系，韦达定理，中点坐标公式，考查计算能力，属于中档题．‎ ‎　‎ ‎10．（5分）已知实数x，y满足，则z=（x﹣1）2+y2的最大值是（　　）‎ A．1 B．9 C．2 D．11‎ ‎【分析】画出平面区域，利用z=（x﹣1）2+y2的几何意义表示为区域内的点与（1，0）的距离的平方最大值求得．‎ ‎【解答】解：x，y满足的平面区域如图：z=（x﹣1）2+y2‎ 的几何意义表示为区域内的点与（1，0）的距离的平方最大值，显然到D 的距离最大，所以z=（x﹣1）2+y2的最大值 z=（1﹣1）2+32=9；‎ 故选B．‎ ‎【点评】本题考查了简单线性规划问题；一般的，正确画出平面区域，利用目标函数的几何意义求最值是常用方法．‎ ‎　‎ ‎11．（5分）设椭圆的左、右焦点分别为F1，F2，P是椭圆上的点．若PF1⊥F1F2，∠F1PF2=60°，则椭圆的离心率为（　　）‎ A． B． C． D．‎ ‎【分析】设F1（﹣c，0），F2（c，0），由题意可得xP=﹣c，代入椭圆方程求得P的坐标，再由解直角三角形的知识，结合离心率公式，解方程可得所求值．‎ ‎【解答】解：设F1（﹣c，0），F2（c，0），由题意可得xP=﹣c，‎ 代入椭圆方程，解得yP=±b=±，‎ 在直角三角形F1PF2中，‎ tan60°==，‎ 即有b2=2ac，‎ 即为a2﹣2ac﹣c2=0，‎ 由e=，可得e2+2e﹣=0，‎ 解得e=（负的舍去）．‎ 故选：B．‎ ‎【点评】本题考查椭圆的方程及运用，考查离心率的求法，注意运用解直角三角形，以及离心率公式，考查运算能力，属于中档题．‎ ‎　‎ ‎12．（5分）已知函数y=f（x）的定义域为R，且对∀x∈R，都有f（﹣x）=f（x），f（x+2）=﹣f（x），当x∈[0，2]时，f（x）=2x﹣1，若关于x的方程f（x）﹣loga（x+2）=0（a＞1）在区间[﹣2，10]上有五个不同的根，则a的取值范围是（　　）‎ A．（1，2） B．（2，+∞） C． D．‎ ‎【分析】由已知可得函数为偶函数且周期为4，另外问题可化为两函数图象的交点个数问题，作出图象可得不等式，解之即可．‎ ‎【解答】解：由对任意的x∈R都有f（﹣x）=f（x），可得f（x）为偶函数，‎ 而f（x﹣4）=f[（x﹣2）﹣2]=﹣f（x﹣2）=f（x），即函数f（x）为周期函数且周期为4，‎ 又当x∈[0，2]时，f（x）=2x﹣1∈[0，3]，‎ 在区间[﹣2，10]上关于x的方程f（x）﹣loga（x+2）=0（a＞1）有五个不同的实数根，‎ 等价于函数f（x）与函数y=loga（x+2）（a＞1）有五个不同的交点，‎ 在同一个坐标系中作出函数的图象，‎ 由题意可得只需，解得8＜a3＜12，‎ 解得2＜a＜．‎ 故选D ‎【点评】本题考查方程根的个数问题，转化为函数图象交点的个数，用数形结合的方式解决问题是关键，属中档题．‎ ‎　‎ 二、填空题（本大题共20分，每小题5分）‎ ‎13．（5分）已知向量=　﹣1　．‎ ‎【分析】根据题意，由向量垂直与向量数量积的关系可得若⊥，则•=2+2k=0，解可得k的值，即可得答案．‎ ‎【解答】解：根据题意，向量=（1，2），=（2，k），‎ 若⊥，则•=2+2k=0，‎ 解可得k=﹣1；‎ 故答案为：﹣1．‎ ‎【点评】本题考查向量数量积的坐标计算，关键是掌握向量垂直与向量数量积的关系．‎ ‎　‎ ‎14．（5分）已知函数f（x）=，则f（f（））　﹣2　．‎ ‎【分析】由已知得f（）=﹣tan=﹣1，从而f（f（））=f（﹣1）=2×（﹣1）3=﹣2．‎ ‎【解答】解：∵函数f（x）=，‎ ‎∴f（）=﹣tan=﹣1，‎ f（f（））=f（﹣1）=2×（﹣1）3=﹣2．‎ 故答案为：﹣2．‎ ‎【点评】本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．‎ ‎　‎ ‎15．（5分）已知椭圆+=1的焦点为F1，F2，P是椭圆上一点，△F1PF2的周长为　32　．‎ ‎【分析】由题意知a=10，b=8，c=6，从而可得|PF1|+|PF2|=2a=20，|F1F2|=2c=12．然后求出三角形的周长．‎ ‎【解答】解：由题意作图如右图，‎ ‎∵椭圆的标准方程为椭圆+=1，‎ ‎∴a=10，b=8，c=6，‎ ‎∴|PF1|+|PF2|=2a=20，‎ ‎|F1F2|=2c=12，‎ ‎∴△PF1F2的周长为20+12=32；‎ 故答案为：32．‎ ‎【点评】本题考查了数形结合的思想应用及椭圆的简单性质的应用，是基础题．‎ ‎　‎ ‎16．（5分）设m，n∈R，若直线（m+1）x+（n+1）y﹣2=0与圆（x﹣1）2+（y﹣1）2=1相切，则m+n的取值范围是　（﹣∞，2﹣2]∪[2+2，+∞）　．‎ ‎【分析】由圆的标准方程找出圆心坐标和半径r，由直线与圆相切时，圆心到直线的距离等于圆的半径，利用点到直线的距离公式列出关系式，整理后利用基本不等式变形，设m+n=x，得到关于x的不等式，求出不等式的解集得到x的范围，即为m+n的范围．‎ ‎【解答】解：由圆的方程（x﹣1）2+（y﹣1）2=1，得到圆心坐标为（1，1），半径r=1，‎ ‎∵直线（m+1）x+（n+1）y﹣2=0与圆相切，‎ ‎∴圆心到直线的距离d==1，‎ 整理得：m+n+1=mn≤（）2，‎ 设m+n=x，则有x+1≤，即x2﹣4x﹣4≥0，‎ ‎∵x2﹣4x﹣4=0的解为：x1=2+2，x2=2﹣2，‎ ‎∴不等式变形得：（x﹣2﹣2）（x﹣2+2）≥0，‎ 解得：x≥2+2或x≤2﹣2，‎ 则m+n的取值范围为（﹣∞，2﹣2]∪[2+2，+∞）．‎ 故答案为：（﹣∞，2﹣2]∪[2+2，+∞）．‎ ‎【点评】此题考查了直线与圆的位置关系，涉及的知识有：点到直线的距离公式，基本不等式，以及一元二次不等式的解法，利用了转化及换元的思想，当直线与圆相切时，圆心到直线的距离等于圆的半径，熟练掌握此性质是解本题的关键．‎ ‎　‎ 三、解答题（解答应写出文字说明，证明过程或演算步骤．）‎ ‎17．（10分）在锐角三角形ABC中，内角A，B，C的对边分别为a，b，c且2asinB=b．‎ ‎（1）求角A的大小；‎ ‎（2）若a=6，b+c=8，求△ABC的面积．‎ ‎【分析】（1）已知等式利用正弦定理化简，求出sinA的值，即可确定出A的度数；‎ ‎（2）利用余弦定理列出关系式，将a，cosA的值代入利用完全平方公式化简，再将b+c的值代入求出bc的值，利用三角形面积公式即可求出三角形ABC面积．‎ ‎【解答】解：（1）将2asinB=b，利用正弦定理化简得：2sinAsinB=sinB，‎ ‎∵sinB≠0，∴sinA=，‎ ‎∵A为锐角，∴A=60°；‎ ‎（2）∵a=6，A=60°，b+c=8，‎ ‎∴由余弦定理得：a2=b2+c2﹣2bccosA，‎ 即36=b2+c2﹣bc=（b+c）2﹣3bc=64﹣3bc，‎ 整理得：bc=，‎ 则S△ABC=bcsinA=．‎ ‎【点评】此题考查了正弦、余弦定理，以及三角形面积公式，熟练掌握定理及公式是解本题的关键．‎ ‎　‎ ‎18．（12分）随机抽取100名学生，他们的身高（单位cm）的频率分布直方图如图所示．‎ ‎（1）求频率分布直方图中的x的值及身高在170cm以上的学生人数；‎ ‎（2）将身高在[170，175），[175，180），[180，185）区间内的学生依次记为A，B，C三组，用分层抽样的方法从这三组中抽取6人，求从这三组分别抽取的人数；‎ ‎（3）在（Ⅱ）的条件下从6名学生中抽取2人，计算B组中至少有1人被抽中的概率．‎ ‎【分析】（1）由频率分布直方图中小矩形面积之和为1，求出x=0.06．由此能出身高在170cm以上的学生人数．‎ ‎（2）身高在[170，175），[175，180），[180，185）区间内的频率分别为：0.3，0.2，0.1，将身高在[170，175），[175，180），[180，185）区间内的学生依次记为A，B，C三组，用分层抽样的方法从这三组中抽取6人，由此能求出从这三组分别抽取的人数．‎ ‎（3）从6名学生中抽取2人，基本事件总数n==15，B组中至少有1人被抽中的对立事件是B组中没有人被抽中，由此利用对立事件概率计算公式能求出B组中至少有1人被抽中的概率．‎ ‎【解答】解：（1）由频率分布直方图得：‎ ‎（0.01+0.03+0.04+x+0.04+0.02）×5=1，‎ 解得x=0.06．‎ ‎∴身高在170cm以上的学生人数为：100×（0.06+0.04+0.02）×5=60人．‎ ‎（2）身高在[170，175），[175，180），[180，185）区间内的频率分别为：0.3，0.2，0.1，‎ 将身高在[170，175），[175，180），[180，185）区间内的学生依次记为A，B，C三组，‎ 用分层抽样的方法从这三组中抽取6人，‎ 从A组抽取的人数为：6×=3人，‎ 从B组抽取的人数为：6×=2人，‎ 从C组抽取的人数为：6×=1人．‎ ‎（3）从6名学生中抽取2人，‎ 基本事件总数n==15，‎ B组中至少有1人被抽中的对立事件是B组中没有人被抽中，‎ ‎∴B组中至少有1人被抽中的概率p=1﹣=．‎ ‎【点评】本题考查频率分布直方图、分层抽样的应用，考查概率的求法，考查频率分布直方图、分层抽样、对立事件概率计算公式等基础知识，考查运用统计知识解决简单实际问题的能力，数据处理能力和运用意识．‎ ‎　‎ ‎19．（12分）已知数列{an}是等差数列，a2=6，a5=18，数列{bn}的前n项和为Tn．且Tn=2bn﹣2‎ ‎（1）求{an}，{bn}的通项公式；‎ ‎（2）令cn=anbn，求数列{cn}的前n项和Sn．‎ ‎【分析】（1）设出公差为d，运用等差数列的通项公式解方程可得首项和公差，即可得到所求{an}的通项公式；再由数列的递推式：b1=T1，n≥2时，bn=Tn﹣Tn﹣1，可得{bn}的通项公式；‎ ‎（2）求得cn=anbn=（4n﹣2）•2n=（2n﹣1）•2n+1‎ ‎，运用数列的求和方法：错位相减法和等比数列的求和公式，计算即可得到所求和．‎ ‎【解答】解：（1）数列{an}是公差为d的等差数列，a2=6，a5=18，‎ 可得a1+d=6，a1+4d=18，‎ 解得d=4，a1=2，‎ 则an=2+4（n﹣1）=4n﹣2；‎ 数列{bn}的前n项和为Tn．且Tn=2bn﹣2，‎ 可得b1=T1=2b1﹣2，解得b1=2，‎ n≥2时，bn=Tn﹣Tn﹣1=2bn﹣2﹣2bn﹣1+2，‎ 即为bn=2bn﹣1，‎ 则bn=2•2n﹣1=2n；‎ ‎（2）cn=anbn=（4n﹣2）•2n=（2n﹣1）•2n+1；‎ 数列{cn}的前n项和Sn=1•22+3•23+…+（2n﹣1）•2n+1，‎ ‎2Sn=1•23+3•24+…+（2n﹣1）•2n+2，‎ 两式相减可得，﹣Sn=22+2（23+…+2n+1）﹣（2n﹣1）•2n+2‎ ‎=4+2•﹣（2n﹣1）•2n+2，‎ 化简可得Sn=（2n﹣3）•2n+2+12．‎ ‎【点评】本题考查等比数列和等差数列的通项公式和求和公式的运用，考查数列的递推式的运用，以及数列的求和方法：错位相减法，考查运算能力，属于中档题．‎ ‎　‎ ‎20．（12分）如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的点．‎ ‎（1）证明：PB∥平面AEC；‎ ‎（2）设AP=1，AD=，三棱锥P﹣ABD的体积V=，求A点到平面PBD的距离．‎ ‎【分析】（1）连接BD交AC于点O，连接EO，推导出EO∥PB．由此能证明PB∥平面AEC．‎ ‎（2）由三棱锥P﹣ABD的体积V=，求出AB=，分别以AD，AB，AP为x，y，z轴建立坐标系，利用向量法能求出A点到平面PBD的距离．‎ ‎【解答】证明：（1）连接BD交AC于点O，连接EO．‎ ‎∵ABCD为矩形，∴O为BD的中点，‎ 又E为PD的中点，∴EO∥PB．‎ ‎∵EO⊂平面AEC，PB⊄平面AEC，‎ ‎∴PB∥平面AEC．‎ 解：（2）∵四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，‎ AP=1，AD=，三棱锥P﹣ABD的体积V=，‎ ‎∴V===，‎ 解得AB=，‎ 分别以AD，AB，AP为x，y，z轴建立坐标系，‎ A（0，0，0），P（0，0，1），B（，0，0），D（0，，0），‎ ‎=（0，0，﹣1），=（，0，﹣1），=（0，，﹣1），‎ 设平面PBD的法向量=（x，y，z），‎ 则，取x=4，得=（4，，3）．‎ ‎∴A点到平面PBD的距离d===．‎ ‎【点评】本题考查线面平行的证明，考查点到平面的距离的求法，考查线段长的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、函数与方程思想、数形结合思想，是中档题．‎ ‎　‎ ‎21．（12分）已知，圆C：x2+y2﹣8y+12=0，直线l：ax+y+2a=0．‎ ‎（1）当a为何值时，直线l与圆C相切；‎ ‎（2）当直线l与圆C相交于A、B两点，且AB=2时，求直线l的方程．‎ ‎【分析】把圆的方程化为标准方程后，找出圆心坐标与圆的半径r，‎ ‎（1）当直线l与圆相切时，圆心到直线的距离d等于圆的半径r，利用点到直线的距离公式表示出圆心到直线l的距离d，让d等于圆的半径r，列出关于a的方程，求出方程的解即可得到a的值；‎ ‎（2）联立圆C和直线l的方程，消去y后，得到关于x的一元二次方程，然后利用韦达定理表示出AB的长度，列出关于a的方程，求出方程的解即可得到a的值．‎ ‎【解答】解：将圆C的方程x2+y2﹣8y+12=0配方得标准方程为x2+（y﹣4）2=4，‎ 则此圆的圆心为（0，4），半径为2．‎ ‎（1）若直线l与圆C相切，则有．解得．‎ ‎（2）联立方程并消去y，‎ 得（a2+1）x2+4（a2+2a）x+4（a2+4a+3）=0．‎ 设此方程的两根分别为x1、x2，‎ 所以x1+x2=﹣，x1x2=‎ 则AB===2‎ 两边平方并代入解得：a=﹣7或a=﹣1，‎ ‎∴直线l的方程是7x﹣y+14=0和x﹣y+2=0．‎ 另解：圆心到直线的距离为d=，‎ AB=2=2，可得d=，‎ 解方程可得a=﹣7或a=﹣1，‎ ‎∴直线l的方程是7x﹣y+14=0和x﹣y+2=0．‎ ‎【点评】此题考查学生掌握直线与圆相切时圆心到直线的距离等于圆的半径，灵活运用韦达定理及两点间的距离公式化简求值，是一道综合题．‎ ‎　‎ ‎22．（12分）已知椭圆C：的右焦点为，离心率为．‎ ‎（1）求椭圆的标准方程；‎ ‎（2）若直线l与椭圆相交于A，B两点，且以AB为直径的圆经过原点O，求证：点O到直线AB的距离为定值；‎ ‎（3）在（2）的条件下，求△OAB面积的最大值．‎ ‎【分析】（1）由c=，根据离心率公式求得a=，则b2=a2﹣c2=1，求出椭圆C的方程；‎ ‎（2）分类讨论，设出直线AB的方程为y=kx+‎ m，代入椭圆方程，利用韦达定理，结合以AB为直径的圆D经过坐标原点，根据点到直线的距离公式，即可得证；‎ ‎（3）分类讨论，求出|AB|的最大值，即可求△OAB面积的最大值 ‎【解答】解：（1）由c=，椭圆的离心率e==，则a=，‎ b2=a2﹣c2=1，‎ ‎∴椭圆的标准方程为：；‎ ‎（2）证明：直线AB斜率存在时，设直线AB的方程为y=kx+m，代入椭圆方程，‎ 消元可得（1+3k2）x2+6kmx+3m2﹣3=0‎ ‎∴x1+x2=﹣，x1x2=，‎ ‎∵以AB为直径的圆D经过坐标原点，∴•=0，‎ ‎∴x1x2+y1y2=0，∴（1+k2）﹣km×+m2=0，‎ ‎∴4m2=3（k2+1）‎ ‎∴原点O到直线的距离为d==，‎ 当直线AB斜率不存在时，由椭圆的对称性可知x1=x2，y1=﹣y2，‎ ‎∵以AB为直径的圆D经过坐标原点，∴•=0，‎ ‎∴x1x2+y1y2=0，∴x12﹣y12=0‎ ‎∵x12+3y12=3，∴|x1|=|y1|=，‎ ‎∴原点O到直线的距离为d=|x1|=，综上，点O到直线AB的距离为定值；‎ ‎（3）解：直线AB斜率存在时，‎ 由弦长公式可得|AB|=‎ ‎=≤=2，‎ 当且仅当k=±时，等号成立，∴|AB|≤2，‎ 直线AB斜率不存在时，|AB|=|y1﹣y2|=＜2，‎ ‎∴△OAB面积=×|AB|×d≤×2×=，‎ ‎∴△OAB面积的最大值为．‎ ‎【点评】本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查韦达定理的运用，考查分类讨论的数学思想，考查学生的计算能力，属于中档题．‎ ‎　‎