2017年高考数学（理科,江苏专版）二轮专题复习与策略 专题限时集训24 第1部分 专题7 选讲部分

2017年高考数学（理科,江苏专版）二轮专题复习与策略 专题限时集训24 第1部分 专题7 选讲部分

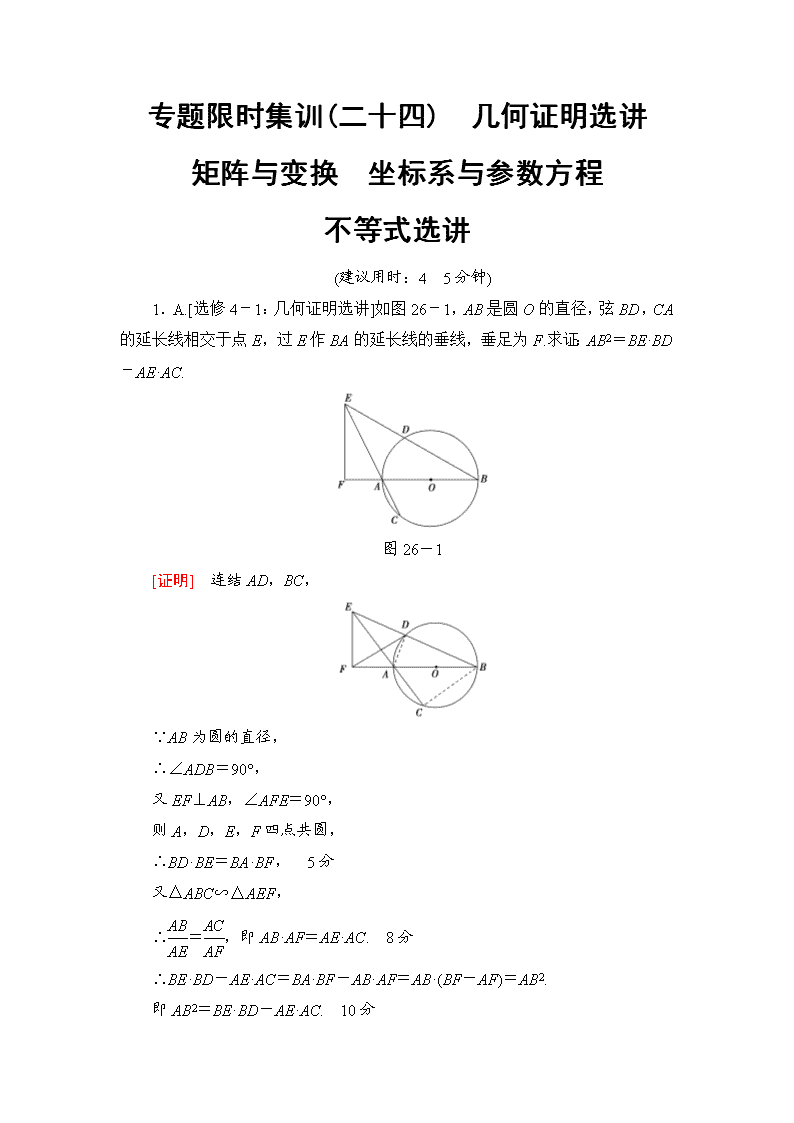
专题限时集训(二十四)　几何证明选讲　矩阵与变换 坐标系与参数方程 不等式选讲 ‎(建议用时：4 5分钟)‎ ‎1．A.[选修4－1：几何证明选讲]如图26－1，AB是圆O的直径，弦BD，CA的延长线相交于点E，过E作BA的延长线的垂线，垂足为F.求证：AB2＝BE·BD－AE·AC.‎ 图26－1‎ ‎[证明]　连结AD，BC，‎ ‎∵AB为圆的直径，‎ ‎∴∠ADB＝90°，‎ 又EF⊥AB，∠AFE＝90°，‎ 则A，D，E，F四点共圆，‎ ‎∴BD·BE＝BA·BF， 5分 又△ABC∽△AEF，‎ ‎∴＝，即AB·AF＝AE·AC. 8分 ‎∴BE·BD－AE·AC＝BA·BF－AB·AF＝AB·(BF－AF)＝AB2.‎ 即AB2＝BE·BD－AE·AC. 10分 B．[选修4－2：矩阵与变换]已知矩阵A＝，A的逆矩阵A－1＝.‎ ‎(1)求a，b的值；‎ ‎(2)求A的特征值．‎ ‎[解]　(1)因为AA－1＝ ‎＝＝，3分 所以解得a＝1，b＝－. 6分 ‎(2)由(1)得A＝，则A的特征多项式f(λ)＝＝(λ－3)(λ－1). 8分 令f(λ)＝0，解得A的特征值λ1＝1，λ2＝3. 10分 C．[选修4－4：坐标系与参数方程]在平面直角坐标系xOy中，已知直线l的参数方程为(t为参数)，椭圆C的参数方程为(θ为参数)．设直线l与椭圆C相交于A，B两点，求线段AB的长．‎ ‎[解]　椭圆C的普通方程为x2＋＝1. 3分 将直线l的参数方程代入x2＋＝1，得2＋＝1，即7t2＋16t＝0， 8分 解得t1＝0，t2＝－.所以AB＝|t1－t2|＝. 10分 D．[选修4－5：不等式选讲]设x为实数，求证：(x2＋x＋1)2≤3(x4＋x2＋1)．‎ ‎[证明]　右－左＝2x4－2x3－2x＋2‎ ‎＝2(x－1)(x3－1)＝2(x－1)2(x2＋x＋1) 5分 ‎＝2(x－1)2≥0，‎ 所以(x2＋x＋1)2≤3(x4＋x2＋1). 10分 ‎2．A.[选修4－1：几何证明选讲]如图26－2，AB为圆O的切线，A为切点，C为线段AB的中点，过C作圆O的割线CED(E在C，D之间)，求证：∠CBE＝∠BDE.‎ 图26－2‎ ‎[证明]　∵直线AB，直线CED分别是⊙O的切线和割线，‎ 由切割线定理得CA2＝CE·CD，‎ ‎∵C为线段AB的中点，∴BC2＝CA2， 5分 ‎∴BC2＝CE·CD，‎ 在△BCE和△DCB中，＝.‎ ‎∵∠BCE＝∠DCB，∴△BCE∽△DCB，‎ ‎∴∠CBE＝∠BDE. 10分 B．[选修4－2：矩阵与变换]已知矩阵M＝的一个特征值为－2，求M2.‎ ‎[解]　将λ＝－2代入＝λ2－(x－1)λ－(x＋5)＝0，得x＝3. 5分 矩阵M＝.‎ ‎∴M2＝. 10分 C．[选修4－4：坐标系与参数方程]已知直线l的参数方程为曲线C的极坐标方程为ρ＝4sin θ，试判断直线l与曲线C的位置关系．‎ ‎[解]　直线l的普通方程为2x－y－2＝0.‎ 曲线C的直角坐标方程为x2＋(y－2)2＝4，它表示圆. 5分 由圆心到直线l的距离d＝＝＜2，得直线l与曲线C相交. 10分 D．[选修4－5：不等式选讲]解不等式2|x－1|≤5－x.‎ ‎[解]　当x≥1时，原不等式等价于2(x－1)≤5－x，‎ 解得x≤，即1≤x≤. 5分 当x＜1时，原不等式等价于2(1－x)≤5－x，‎ 解得x≥－3，即－3≤x＜1.‎ 综上可知，原不等式的解集为. 10分