2014高考数学 必考热点分类集中营3
2014 高考数学必考热点分类集中营 3
2.【2010 新课标全国】已知命题 1p :函数 2 2x xy 在 R 为增函数,
2p :函数 2 2x xy 在 R 为减函数,则在命题 1q : 1 2p p , 2q : 1 2p p , 3q : 1 2p p
和 4q : 1 2p p 中,真命题是
(A) 1q , 3q (B) 2q , 3q (C) 1q , 4q (D) 2q , 4q
3. 【2012 新课标全国文】当 0
0,a≠1).
3.幂函数:通过实例,了解幂函数的概念;结合函数 y=x,y=x2,y=x3,y=
1
x,
1
2y x 的
图象,了解它们的变化情况.
4.解读考纲: 指数函数、对数函数是新课标考查的重要方面.指数函数主要题型有:指数函
数的图象与性质、幂值的大小比较、由指数函数复合而成的综合问题.对数是常考常变的内
容,主要题型是对数函数的图象性质、对数运算法则、对数函数定义域.幂函数新课标要求
较低,只要掌握幂函数的概念、图象与简单性质,仅限于几个特殊的幂函数.反函数新课标
比原大纲要求有较大幅度降低,只要知道指数函数与对数函数互为反函数及定义域、图象的
关系即可,不宜过分延伸.因此命题会主要集中在指数、对数的运算性质,指、对函数的图
象与性质及数值大小比较等问题上,结合数形结合、分类讨论、函数与方程的思想予以考查,
与方程、不等式、分段函数、数列、导数、三角函数等相联系,仍将是命题的重点.
【回归课本整合】
1 指数式、对数式:
m
n mna a , 1m
n
m
n
a
a
,, 0 1a , log 1 0a , log 1a a , lg 2 lg5 1 , log lne x x ,
log ( 0, 1, 0)b
aa N N b a a N , loga Na N , loglog log
c
a
c
bb a
,
log logm
n
aa
nb bm
.
2.指数、对数值的大小比较:(1)化同底后利用函数的单调性;(2)作差或作商法;(3)利
用中间量(0 或 1);(4)化同指数(或同真数)后利用图象比较.
3.指数函数:
(1)指数函数图象和性质
1a 0 1a
图象
性质
定义域: R 值域: 0, 过定点 0,1
在 R 上是增函数 在 R 上是减函数
当 0x , 1y ;
当 0x , 0 1y .
当 0x , 0 1y ;
当 0x , 1y .
抽象
形式 ( ) ( ) ( ), ( ) ( ) ( )f x y f x f y f x y f x f y
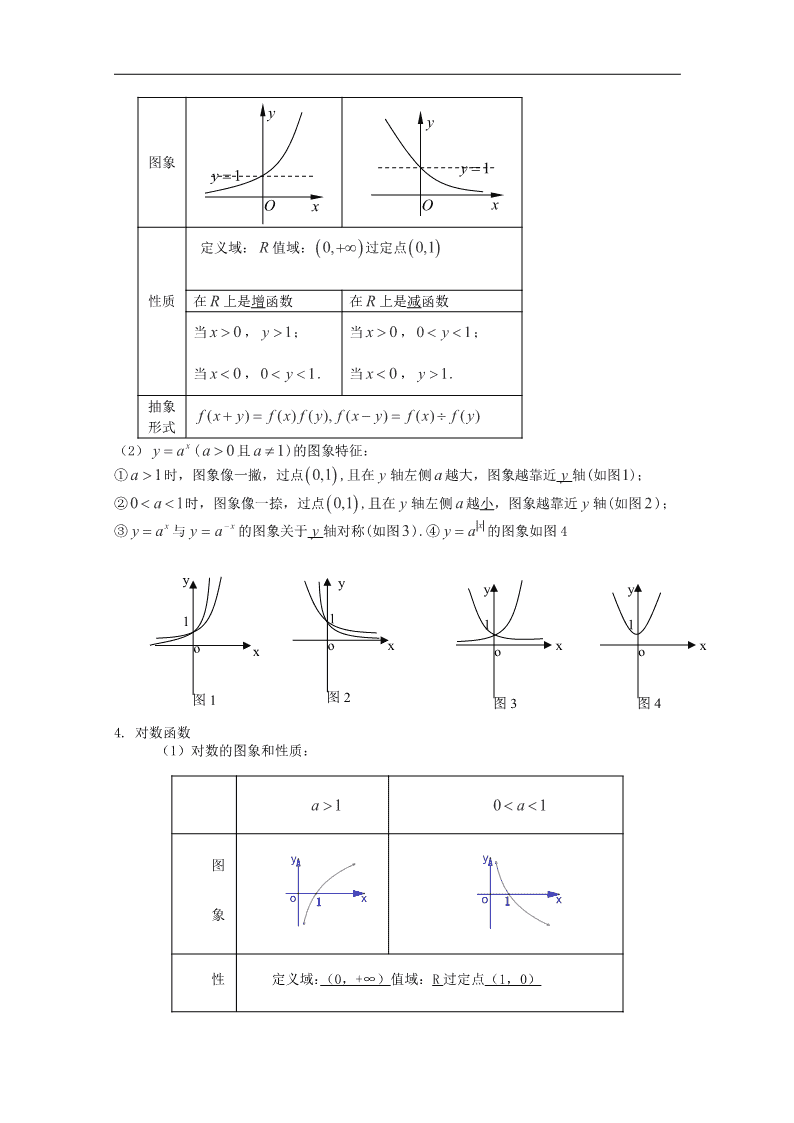
(2) xy a ( 0a 且 1a )的图象特征:
① 1a 时,图象像一撇,过点 0,1 ,且在 y 轴左侧 a 越大,图象越靠近 y 轴(如图1);
② 0 1a 时,图象像一捺,过点 0,1 ,且在 y 轴左侧 a 越小,图象越靠近 y 轴(如图 2 );
③ xy a 与 xay 的图象关于 y 轴对称(如图3).④ xy a 的图象如图 4
x
y
o
图 2
1
x
y
o
图 1
1
x
y
o
图 3
1
x
y
o
图 4
1
4. 对数函数
(1)对数的图象和性质:
1a 0 1a
图
象
�
1
o
y
x
�
1
o
y
x
性 定义域:(0,+∞)值域:R 过定点(1,0)
xO
y
1y 1y
O x
y
( 2 )
)10(log aaxy a 且 的图象特征:
① 1a 时,图象像一撇,过 1,0 点,在 x 轴上方 a 越大越靠近 x 轴;
② 0 1a 时,图象像一捺,过 1,0 点,在 x 轴上方 a 越小越靠近 x 轴.
③ xay ( 1, 1a a )与 xy alog 互为反函数,图象关于 y x 对称;如图 2
④ log ( 1)ay x a 的图象 3.⑤ log ( 1)ay x a 的图象 4.
x
y
o
图 2
1
x
y
o
图 1
1
x
y
o
图 3
1 x
y
o
图 4
1-1
5.幂函数的定义和图象
(1)定义:形如 y=xα的函数叫幂函数(α为常数)要重点掌握α=1,2,3,
1
2,-1,0,-
1
2,
-2 时的幂函数。
(2)图象:(只作出第一象限图象)
.
(3)性质:
质 )1,0(x 时 0y
),1( x 时 0y
)1,0(x 时 0y
),1( x 时 0y
在(0,+∞)上是增函数 在(0,+∞)上是减函数
形式 ( ) ( ) ( ) ( ) ( ) ( )f xy f x f y f x y f x f y ;
(1)当α>0 时,幂函数图象都过 (0,0)点和 (1,1)点;且在第一象限都是增 函数;当 0<α
<1 时曲线上凸;当α>1 时,曲线下凸;α=1 时,为过(0,0)点和(1,1)点的直线 (2)当α<0
时,幂函数图象总经过 (1,1) 点,且在第一象限为减函数.
(3)α=0 时 y=x0,表示过(1,1)点平行于 x 轴的直线(除去(0,1)点).
6. 常见复合函数类型
y=af(x)(a>0 且 a≠1) y=logaf(x)(a>0 且 a≠1)
定义域 t=f(x)的定义域 t=f(x)>0 的解集
值域
先求 t=f(x)的值域,再由 y
=at 的单调性得解
先求 t 的取值范围,再由 y=logat 的单调性得解
y=af(x)(a>0 且 a≠1) y=logaf(x)(a>0 且 a≠1)
过定点
令 f(x)=0,得 x=x0,则过定
点(x0,1)
令 f(x)=1,得 x=x0,则过定点(x0,0)
单调区
间
先求 t=f(x)的单调区间,再
由同增异减得解
先求使 t=f(x)>0 恒成立的单调区间,再由同增异减
得解
【方法技巧提炼】
1.指数运算的实质是指数式的积、商、幂的运算,对于指数式的和、差应充分运用恒等变形
和乘法公式;对数运算的实质是把积、商、幂的对数转化为对数的和、差、倍.
2.指数函数 y=ax(a>0,且 a≠1)与对数函数 y=logax(a>0,且 a≠1)互为反函数,应从概
念、图象和性质三个方面理解它们之间的联系与区别.
3.明确函数图象的位置和形状要通过研究函数的性质,要记忆函数的性质可借助于函数的图
象.因此要掌握指数函数和对数函数的性质首先要熟记指数函数和对数函数的图象.
4.求解与指数函数有关的复合函数问题时,首先要熟知指数函数的定义域、值域、单调性等
相关性质,其次要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同
增异减”这一性质分析判断,最终将问题归纳为与内层函数相关的问题加以解决.
【考场经验分享】
1.此类题一般在选择题的中间位置,难度为中档,应该是得分的题目。在解题时注意解答选
择题常用的方法:验证法和排除法的应用。
2. 指数函数 y=ax(a>0,a≠1)的图象和性质与 a 的取值有关,要特别注意区分 a>1 与 00 且 a≠1)与对数式 logaN=b(a>0 且 a≠1,N>0)的关系以及这两种形式
的互化是对数运算法则的关键.
5.在运算性质 logaMn=nlogaM(a>0 且 a≠1,M>0)时,要特别注意条件,在无 M>0 的条件下
应为 logaMn=nloga|M|(n∈N*,且 n 为偶数).
6.幂函数的图象一定会出现在第一象限,一定不会出现在第四象限,至于是否出现在第二、
三象限,要看函数的奇偶性;幂函数的图象最多只能同时出现在两个象限内;如果幂函数图
象与坐标轴相交,则交点一定是原点.
【新题预测演练】
1.【山东省实验中学 2013 届高三第二次诊断性测试】已知幂函数 )(xf 的图像经过(9,3),
则 )1()2( ff =
A.3 B. 21 C. 12 D.1
3.【四川省绵阳南山中学高 2013 级第五期零诊考试】下列函数中,既是偶函数又在(0,+∞)
上单调递增的函数是( )
A.y=x3 B.y=|x|+1 C.y=-x2+1 D.y=2-∣x∣
4. 【 2013 届 贵 州 天 柱 民 中 、 锦 屏 中 学 、 黎 平 一 中 、 黄 平 民 中 四 校 联 考 】 设
2lg , (lg ) , lga e b e c e= = = ,则( )
A. a b c> > B. c a b> > C. a c b> > D. c b a> >
5.【安徽省 2013 届高三开年第一考文】已知函数 2( )f x ax bx c ,且 ( ) 0f x 的解集
6. 【 2013 年 乌 鲁 木 齐 地 区 高 三 年 级 第 一 次 诊 断 性 测 验 试 卷 】 函 数
,则 是
A.奇函数 B.偶函数 C.既不是奇函数又不是偶函数D.既是奇函数又是偶函数
7.【北京市海淀区北师特学校 2013 届高三第四次月考】下列函数中,是奇函数且在区间 (0,1)
内单调递减的函数是 ( )
A. 1
2
logy x B. 3y x C. 1y x
D. xy tan
8. 【 北 京 市 昌 平 区 2013 届 高 三 上 学 期 期 末 理 】已 知 函 数 : ① , ②
,③ .则以下四个命题对已知的三个函数都能成立的是
命题 是奇函数; 命题 在 上是增函数;
命题 ; 命题 的图像关于直线 对称
A.命题 B.命题 C.命题 D.命题
9.[安徽省宣城市 6 校 2013 届高三联合测评考]函数 1
xy e x
的图像大致是( )
10.【云南玉溪一中 2013 届第四次月考试卷】函数 2( ) xf x x a
的图象不可能...是 ( )
11.【2013 年长春市高中毕业班第一次调研测试】
若直角坐标平面内的两个不同点 M 、 N 满足条件:
① M 、 N 都在函数 ( )y f x 的图像上; ② M 、 N 关于原点对称.
则称点对[ , ]M N 为函数 ( )y f x 的一对“友好点对”.
(注:点对[ , ]M N 与[ , ]N M 为同一“友好点对”)
已知函数 3
2
log ( 0)
( )
4 ( 0)
x x
f x
x x x
≤
,此函数的“友好点对”有
A. 0 对 B. 1 对 C. 2 对 D. 3 对
12.【山东省实验中学 2013 届高三第二次诊断性测试】方程 xa x 2)2(log
2
1 有解,则 a 的
最小值为
A.2 B.1 C.
2
3 D.
2
1
14.【河北省唐山市 2012-2013 学年度高三年级摸底考试】
下列函数中,既是偶函数,又在区间(0,3)内是增函数的是
(A) y= 2 2x x (B) y=cosx
(C)y= 0.5log | |x (D) y=x+x-1
15.【2012 河北省名校名师俱乐部高三第二次调研考试】已知函数 ( ) | lg |f x x , 0a b ,
( ) ( )f a f b ,则
2 2a b
a b
的最小值等于
A. 2 2 B. 5 C. 2 3 D. 2 3
16. 【 北 京 市 丰 台 区 2013 届 高 三 上 学 期 期 末 理 】 已 知 函 数 f(x)= , 且
,集合 A={m|f(m)<0},则
(A) 都有 (B) 都有
(C) 使得 f(m0+3)=0 (D) 使得 f(m0+3)<0
17.【安徽省黄山市 2013 届高中毕业班第一次质量检测】
已知函数 lg( )x xf x xa b 中,常数 1 0 1a b a b a b 、 满足 ,且 ,那么
1f x 的解集为
A. (0 1), B. (1 ) , C. (1 10), D. (10 ) ,
18.【2013 届浙江省重点中学协作体高三摸底测试】
若函数 2( )f x x ax b 有两个零点 cos ,cos ,其中 , (0, ) ,那么在 ( 1), (1)f f 两个函数
值中
A.只有一个小于 1 B.至少有一个小于 1
C.都小于 1 D.可能都大于 1
19.【山东省实验中学 2013 届高三第二次诊断性测试】若函数对于函数 qpxxxxf ||)( ,
现给出四个命题:
① 0q 时, )(xf 为奇函数
② )(xfy 的图象关于 ),0( q 对称
③ 0,0 qp 时,方程 0)( xf 有且只有一个实数根
④方程 0)( xf 至多有两个实数根
其中正确命题的序号为 .
20.【上海市嘉定 2013 届高三一模】设 m、nR,定义在区间[m, n]上的函数
|)|4(log)( 2 xxf 的值域是[0, 2],若关于 t 的方程 01||
2
1 mt (tR)有实数解,
则 m+n 的取值范围是 .
21.【北京市西城区 2013 届高三上学期期末理】已知函数 的定义域为 .若 常数
,对 ,有 ,则称函数 具有性质 .给定下列三
个函数: ① ; ② ; ③ .
其中,具有性质 的函数的序号是______.