高考数学专题复习：《函数的应用》单元测试题2

高考数学专题复习：《函数的应用》单元测试题2

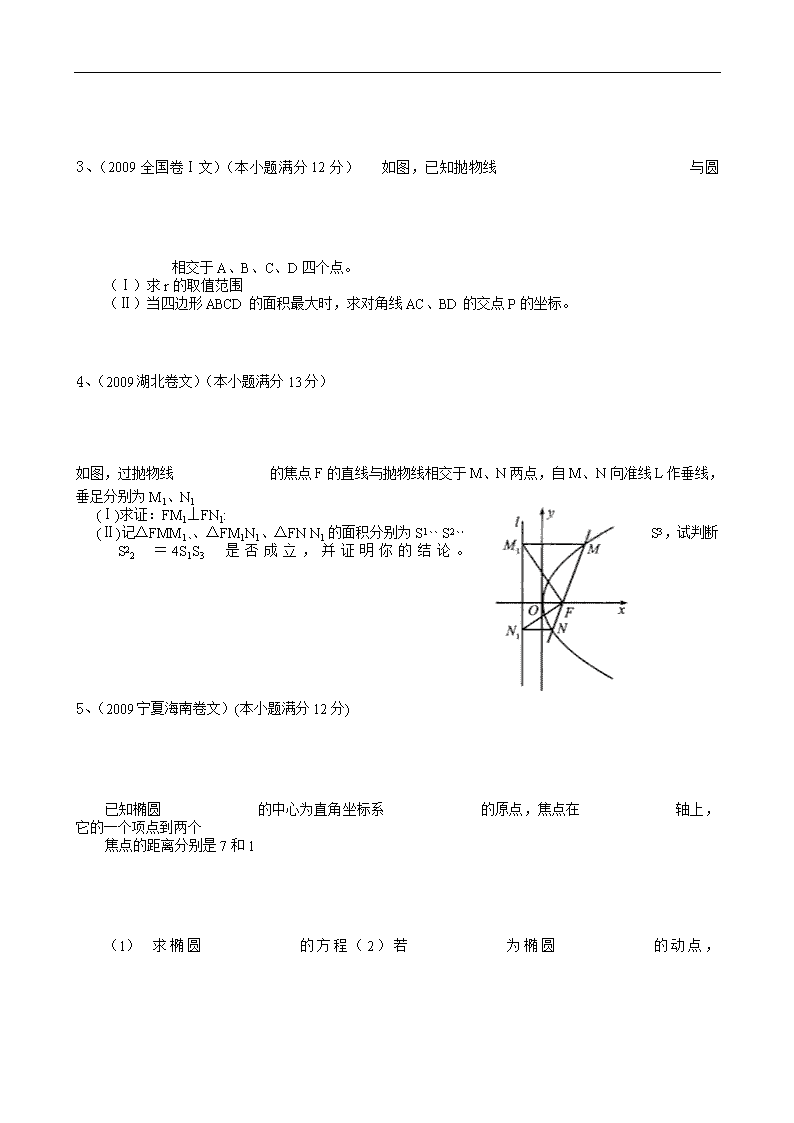
‎《函数的应用》单元测试题2‎ 一、解答题 ‎1、（2009陕西卷文）（本小题满分12分）已知双曲线C的方程为，离心率，顶点到渐近线的距离为。‎ ‎（1）求双曲线C的方程；(2)如图，P是双曲线C上一点，A，B两点在双曲线C的两条渐近线上，且分别位于第一、二象限，若，求面积的取值范围。‎ ‎2、（2009年上海卷理）（本题满分16分） 已知双曲线设过点的直线l的方向向量 ‎ ‎（1） 当直线l与双曲线C的一条渐近线m平行时，求直线l的方程及l与m的距离；‎ ‎（2） 证明：当>时，在双曲线C的右支上不存在点Q，使之到直线l的距离为。‎ ‎3、（2009全国卷Ⅰ文）（本小题满分12分） 如图，已知抛物线与圆相交于A、B、C、D四个点。‎ ‎（Ⅰ）求r的取值范围 ‎（Ⅱ）当四边形ABCD的面积最大时，求对角线AC、BD的交点P的坐标。‎ ‎4、（2009湖北卷文）（本小题满分13分）‎ 如图，过抛物线的焦点F的直线与抛物线相交于M、N两点，自M、N向准线L作垂线，垂足分别为M1、N1 ‎ (Ⅰ)求证：FM1⊥FN1:‎ ‎(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为S1、、S2、，S3，试判断S22＝4S1S3是否成立，并证明你的结论。 ‎ ‎5、（2009宁夏海南卷文）(本小题满分12分)‎ 已知椭圆的中心为直角坐标系的原点，焦点在轴上，它的一个项点到两个 焦点的距离分别是7和1‎ ‎（1） 求椭圆的方程（2）若为椭圆的动点，‎ 为过且垂直于轴的直线上的点，（e为椭圆C的离心率），求点的轨迹方程，并说明轨迹是什么曲线。‎ ‎6、（2009重庆卷文）（本小题满分12分）已知以原点为中心的双曲线的一条准线方程为，离心率．‎ ‎（Ⅰ）求双曲线方程；（Ⅱ）如题（20）图，点的坐标为，是圆上的点，点在双曲线右支上，求的最小值，并求此时点的坐标； ‎ ‎7、（2009上海卷文）（本题满分16分）已知双曲线C的中心是原点，右焦点为F，一条渐近线m:,设过点A的直线l的方向向量。‎ ‎（1） 求双曲线C的方程； ‎ ‎（2） 若过原点的直线，且a与l的距离为，求K的值；‎ ‎（3） 证明：当时，在双曲线C的右支上不存在点Q，使之到直线l的距离为.‎ ‎8、（2009福建卷文）（本小题满分14分）已知直线经过椭圆 的左顶点A和上顶点D，椭圆的右顶点为，点和椭 圆上位于轴上方的动点，直线，与直线‎10‎ ‎:‎ ‎3‎ lx = 分别交于两点。‎ ‎（I）求椭圆的方程； ‎ ‎（II）求线段MN的长度的最小值； ‎ ‎（III）当线段MN的长度最小时，在椭圆上是否存在这 样的点，使得的面积为？若存在，确定点的个数，若不存在，说明理由 ‎ ‎ 以下是答案 一、解答题 ‎1、解法1（Ⅰ）由题意知，双曲线C的顶点（0，a）到渐近线，所以所以 由所以曲线的方程是 ‎（Ⅱ）由（Ⅰ）知双曲线C的两条渐近线方程为 设 由 将P点的坐标代入 因为 又，所以 记则 由又S（1）=2，‎ 当时，面积取到最小值，当时，面积取到最大值 所以面积范围是 解答2（Ⅰ）由题意知，双曲线C的顶点（0，a）到渐近线，‎ 由 所以曲线的方程是.‎ ‎（Ⅱ）设直线AB的方程为由题意知 由 由 将P点的坐标代入得 设Q为直线AB与y轴的交点，则Q点的坐标为（0，m）‎ ‎=‎ ‎2、解：（1）双曲线C的渐近线 直线l的方程 ‎ 直线l与m的距离 ‎ ‎（2）设过原点且平行与l的直线 则直线l与b的距离当 ‎ 又双曲线C的渐近线为 双曲线C的右支在直线b的右下方，‎ 双曲线右支上的任意点到直线的距离为。‎ 故在双曲线的右支上不存在点，使之到直线的距离为。‎ ‎[ 证法二] 双曲线的右支上存在点到直线的距离为，‎ 则由（1）得， ‎ 设 ‎ 当，0‎ 将 代入（2）得 ‎ 方程（*）不存在正根，即假设不成立 ‎ 故在双曲线C的右支上不存在Q，使之到直线l 的距离为 ‎3、解：（Ⅰ）将抛物线代入圆的方程，消去，整理得．．．．．．．．．．．．．（1）‎ 抛物线与圆相交于、、、四个点的充要条件是：方程（1）有两个不相等的正根 ‎∴即。解这个方程组得 ‎.‎ ‎（II） 设四个交点的坐标分别为、、、。‎ 则由（I）根据韦达定理有，‎ 则 ‎ ‎ 令，则 下面求的最大值。‎ 方法1：由三次均值有：‎ ‎ ‎ ‎ 当且仅当，即时取最大值。经检验此时满足题意。‎ 法2：设四个交点的坐标分别为、、、‎ 则直线AC、BD的方程分别为 解得点P的坐标为。设，由及（Ⅰ）得 ‎ 由于四边形ABCD为等腰梯形，因而其面积 则将，代入上式，并令，等 ‎，‎ ‎∴，令得，或（舍去）当时，；当时；当时，‎ 故当且仅当时，有最大值，即四边形ABCD的面积最大，故所求的点P的坐标为。 ‎ ‎4、解（1）证法1：由抛物线的定义得 ‎ ‎ ‎ ‎ 如图，设准线l与的交点为， ‎ ‎ ‎ 而 即 故 证法2：依题意，焦点为准线l的方程为 设点M,N的坐标分别为直线MN的方程为，则有 由 得于是，，‎ ‎，故 ‎（Ⅱ）成立，证明如下：‎ 证法1：设，则由抛物线的定义得 ‎，于是 ‎ ‎ 将与代入上式化简可得 ，此式恒成立。故成立。‎ 证法2：如图，设直线M的倾角为，‎ 则由抛物线的定义得 于是 在和中，由余弦定理可得 由（I）的结论，得 即，得证。‎ ‎ ‎ ‎5、解：（Ⅰ）设椭圆长半轴长及分别为a,c由已知得 ‎ ‎{ 解得a=4,c=3, 21世纪教育网 ‎ 所以椭圆C的方程为 ‎ ‎（Ⅱ）设M（x,y）,P(x,),其中由已知得 而，故 ①‎ 由点P在椭圆C上得 代入①式并化简得 所以点M的轨迹方程为轨迹是两条平行于x轴的线段. ‎ ‎6、解：（Ⅰ）由题意可知，双曲线的焦点在轴上，故可设双曲线的方程为，设，由准线方程为得，由 得 解得 从而，该双曲线的方程为；‎ ‎（Ⅱ）设点D的坐标为，则点A、D为双曲线的焦点，‎ 所以 ，是圆上的点，其圆心为，半径为1，故 从而 当在线段CD上时取等号，此时的最小值为 直线CD的方程为，因点M在双曲线右支上，故 由方程组 解得 ‎ ‎ 所以点的坐标为。‎ ‎7、【解】（1）设双曲线的方程为 ‎ ，解额双曲线的方程为 ‎（2）直线，直线 由题意，得，解得 ‎（3）【证法一】设过原点且平行于的直线 则直线与的距离当时， ‎ 又双曲线的渐近线为 双曲线的右支在直线的右下方，‎ ‎ 双曲线右支上的任意点到直线的距离大于。‎ 故在双曲线的右支上不存在点，使之到直线的距离为 ‎【证法二】假设双曲线右支上存在点到直线的距离为，‎ 则由（1）得 设，当时，；‎ 将代入（2）得 ‎， ‎ ‎ 方程不存在正根，即假设不成立，‎ 故在双曲线的右支上不存在点，使之到直线的距离为 ‎8、解法一：（I）由已知得，椭圆的左顶点为上顶点为 ‎ 故椭圆的方程为 ‎（Ⅱ）直线AS的斜率显然存在，且，故可设直线的方程为，从而由得0‎ 设则得，从而 ‎ 即又由得故又；当且仅当，即时等号成立 时，线段的长度取最小值 ‎（Ⅲ）由（Ⅱ）可知，当取最小值时，‎ ‎ 此时的方程为 ‎ 要使椭圆上存在点，使得的面积等于，只须到直线的距离等于，所以 在平行于且与距离等于的直线上。‎ 设直线则由解得或 ‎