数学理卷·2017届山东省临沂市高三上学期期末考试（2017

数学理卷·2017届山东省临沂市高三上学期期末考试（2017

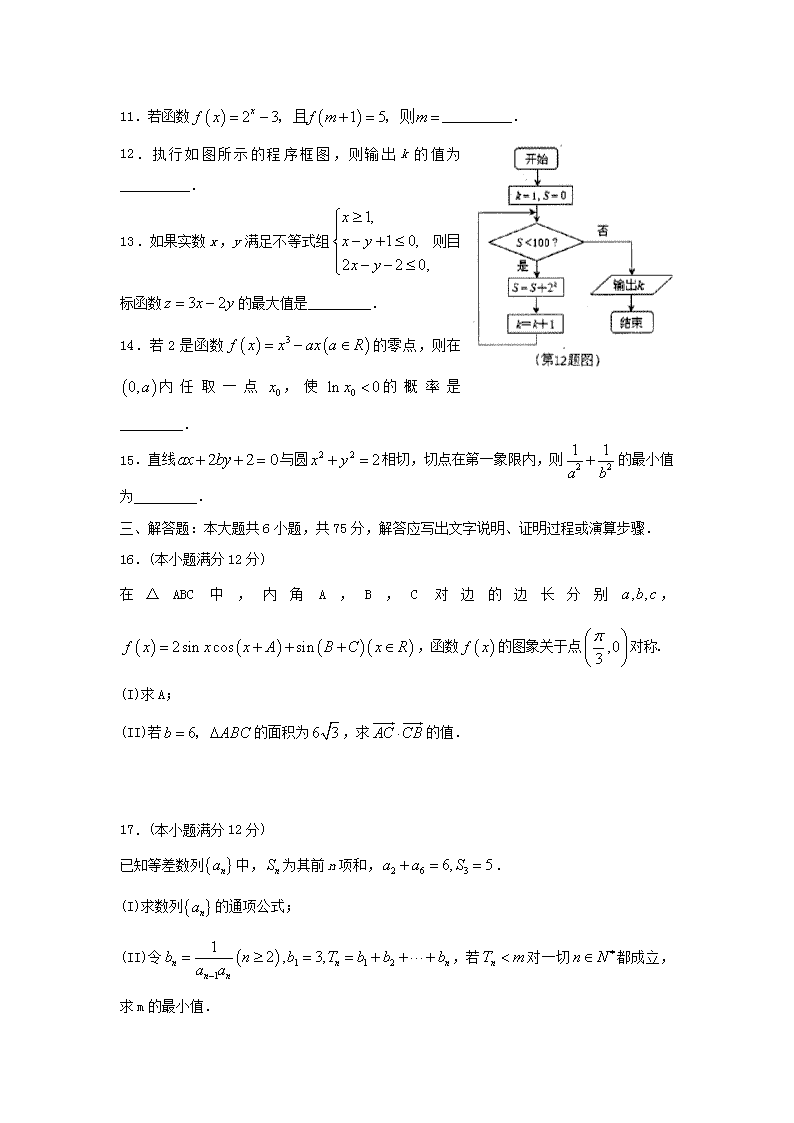
高三年级期末教学质量抽测试题 理科数学 ‎ 2017．01 ‎ ‎ 本试卷分第I卷(选择题)和第II卷(非选择题)两部分．满分150分．考试时间120分钟．‎ 第I卷(选择题 共50分)‎ 一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选顶中，只有一项是符合题目要求的． ‎ ‎1．i为虚数单位，复数在复平面内对应的点到原点的距离为( ) ‎ A． B． C． D．1‎ ‎2．已知集合A=，B=，且A∩B=，则A∪B=( )‎ A． B． C． D．‎ ‎3．下列说法正确的是( )‎ A．命题“2≥1”是假命题 B．命题“”的否定是：<0‎ C．命题“若，则”的否命题是“若，则a≤b”‎ D．“”是“”充分不必要条件 ‎4．函数的图象的大致形状是( )‎ ‎5．某兴趣小组有男生20人，女生10人，从中抽取一个容量为5的样本，恰好抽到2名男生和3名女生，则①该抽样可能是系统抽样；②该抽样可能是随机抽样：③该抽样一定不是分层抽样；④本次抽样中每个人被抽到的概率都是．‎ 其中说法正确的为( )‎ A．①②③ B．②③ C．②③④ D．③④‎ ‎6．设D，E，F分别△ABC的三边AB，BC，CA的中点，则=( )‎ A． B． C． D．‎ ‎7．一个圆柱的正视图是面积为6的矩形，它的侧面积为( )‎ A． B． C． D．‎ ‎8．若，则（ ）‎ A． B． C． D．‎ ‎9．已知过双曲线的左焦点和虚轴端点E的直线交双曲线右支于点P，若E为线段EP的中点，则该双曲线的离心率为( )．‎ A． B． C． D．‎ ‎10．函数的部分图象如图所示，其中，给出下列结论：‎ ‎①最小正周期为；②；③函数是偶函数；‎ ‎④；⑤.‎ 其中正确结论的个数是( )‎ A．5 B．4 C．3 D．2‎ 第Ⅱ卷(非选择题 共100分)‎ 二、填空题：本大题共5小题，每小题5分，共25分，把答案填在题中横线上．‎ ‎11．若函数__________．‎ ‎12．执行如图所示的程序框图，则输出k的值为__________．‎ ‎13．如果实数x，y满足不等式组则目标函数的最大值是_________．‎ ‎14．若2是函数的零点，则在内任取一点，使的概率是_________．‎ ‎15．直线与圆相切，切点在第一象限内，则的最小值为_________．‎ 三、解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤．‎ ‎16．(本小题满分12分)‎ 在△ABC中，内角A，B，C对边的边长分别，，函数的图象关于点对称.‎ ‎(I)求A；‎ ‎(II)若的面积为，求的值．‎ ‎17．(本小题满分12分) ‎ 已知等差数列中，为其前n项和，．‎ ‎(I)求数列的通项公式； ‎ ‎(II)令，若对一切都成立，求m的最小值．‎ ‎18．(本小题满分12分) ‎ 某高中学校为展示学生的青春风采，举办了校园歌手大赛，该大赛分为预赛和决赛两个阶段，参加决赛的学生按照抽签方式决定出场顺序，通过预赛，选拔出甲、乙等5名学生参加决赛． ‎ ‎(I)求决赛中学生甲、乙恰好排在前两位的概率；‎ ‎(Ⅱ)若决赛中学生甲和学生乙之间间隔的人数记为X，求X的分布列及数学期望EX．‎ ‎19．(本小题满分12分)‎ 如图，在四棱锥中，底面ABCD是直角梯形，AD// BC，，平面底面ABCD，Q为AD的中点，.‎ ‎(I)求证：平面平面PAD；‎ ‎(II)在棱PC上是否存在一点M，使二面角?若存在，确定M的位置；若不存在，请说明理由．‎ ‎20．(本题满分13分)‎ 已知椭圆，其短轴的一个端点与两个焦点构成面积为的正三角形，过椭圆C的右焦点作斜率为的直线l与椭圆C相交于A、B两点，线段AB的中点为P．‎ ‎(I)求椭圆C的标准方程；‎ ‎(II)过点P垂直于AB的直线与x轴交于点D，试求的取值范围。‎ ‎21．(本题满分14分)‎ ‎ 设函数，且存在两个极值点，其中。‎ ‎(I)求实数a的取值范围； ‎ ‎(II)证明不等式： ‎ 高三年级期期末教学质量抽测试题 理数 答案 2017.1‎ 一、选择题：本大题共10小题，每小题5分，共50分.‎ ‎1．C 2．D 3．D 4．B 5．A 6．C 7．B 8．A 9．B 10．D 二、填空题：本大题共5小题，每小题5分，满分25分． ‎ ‎11． 12．7 13．1 14． 15．‎ 三、解答题：本大题共6小题，共75分． ‎ ‎16．（本小题满分12分）‎ 解：（Ⅰ）‎ ‎-------------1分 ‎ -----------------------------------------3分 因为函数的图象关于点对称．所以，---------4分 即，又，-------------------5分 ‎（Ⅱ）∵，△ABC的面积为，‎ ‎，，------------------------------6分 ‎，---------------------------7分 ‎． ---------------------------8分 ‎，---------------------------10分 ‎．---------12分 ‎17．解：(Ⅰ) 设等差数列{an}的公差为d，‎ 由a2＋a6＝6，S3＝5得，---------------------------2分 解得-----------------------------------------------4分 ‎∴an＝n＋.------------------------------------------------5分 ‎(Ⅱ)当n≥2时，bn＝＝＝,--------6分 当n＝1时，上式同样成立，-----------------------------------7分 ‎∴Sn＝b1＋b2＋…＋bn ‎＝＝,----------------9分 又随n递增，且＜·1≤m，----------------10分 又m∈，∴m≥5，----------------------------------------11分 ‎∴ m的最小值为5．--------------------------------------------12分 ‎18．解：（Ⅰ）设“学生甲、乙恰好排在前两位”为事件，则 ‎．--------------------------------------3分 ‎(Ⅱ)随机变量的可能的值为0，1，2，3．---------------------4分 ‎------------------------------------5分 ‎----------------------------------7分 ‎--------------------------------9分 ‎-----------------------------------10分 随机变量的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎ ‎ ‎-----------------------------------------------------11分 因为．------------------12分 ‎18．（本小题满分12分）‎ 解： (Ⅰ) Q为AD的中点，‎ 所以四边形是平行四边形，-----------------------1分 即 -----------------------2分 ‎∵PA=PD，‎ 又-----------------------4分 所以平面PQB⊥平面PAD. -------------5分 ‎(Ⅱ) ∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD，‎ 又，且 ‎ -----------------------6分 以为原点，为轴，为轴，为轴建立空间直角坐标系，‎ 则平面的一个法向量---7分 设满足条件的点存在，则 令其中 在平面中，----------9分 设平面的一个法向量 则有 平面的一个法向量 -----------------------10分 二面角为 解得 -----------------------11分 所以满足条件的点存在，是棱的靠近点的四等分点. ------12分 ‎20．（本小题满分13 分）‎ 解：（Ⅰ）设右焦点的坐标为，易知面积为的正三角形的边长为2，‎ 依题意知，-------------2分 所以，椭圆的方程为．---------------------------3分 ‎（Ⅱ）设过椭圆的右焦点的直线的方程为，‎ 将其代入中得，，-------4分 其中，，设，‎ 则，----------------------------5分 ‎，----------------6分 因为为线段的中点，所以，点的坐标为．‎ 故点的坐标为，-----------------------------7分 又直线的斜率为，‎ 直线的方程为，------------------9分 令得，，则点的坐标为，‎ 所以，，-------10分 又 ‎．-----------------11分 所以，，-------------12分 又 所以，的取值范围是------------------------------13分 ‎21．（本小题满分14 分）‎ 解：（Ⅰ）由题意，，-----------------1分 ∵函数存在两个极值点，且， ∴关于的方程，‎ 即在内有两个不相等实根．--------------2分 令，‎ 则 -----------------------------------------3分 解得．所以，实数的取值范围．-------------4分 ‎（Ⅱ）由（Ⅰ）知 ∴，---------10分 令，则，且， ‎ 令，则------------------11分 ------12分 ∴，‎ ‎∵，∴即在上是减函数， ∴，∴在上是增函数，------------13分 ‎∴，即，‎ 所以，．------------------------------------14分