数学理卷·2018届四川省泸州市高三第二次教学质量检测性考试（2018

数学理卷·2018届四川省泸州市高三第二次教学质量检测性考试（2018

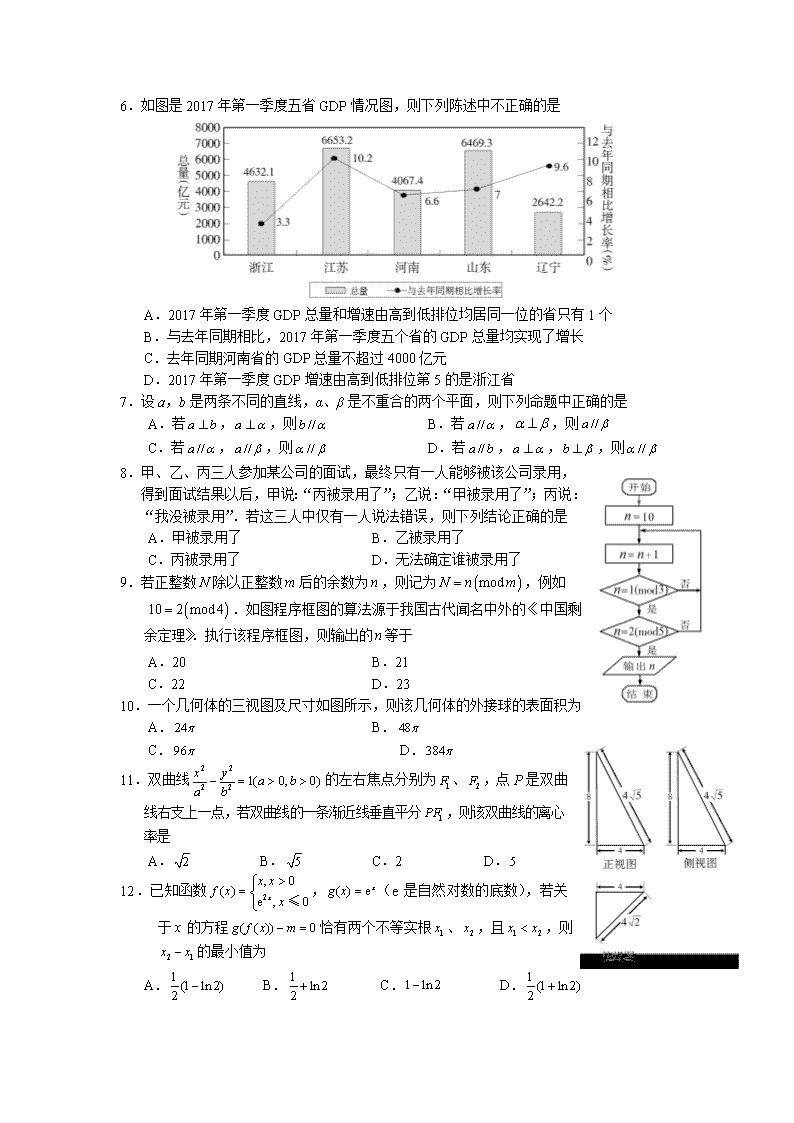
泸州市高 2015 级（2018 届）第二次教学质量诊断性考试 数 学（理科） 本试卷分第 I 卷（选择题）和第 II 卷（非选择题）两部分. 第 I 卷 1 至 2 页，第 II 卷 3 至 4 页.共 150 分.考试时间 120 分钟. 第 I 卷 （选择题 共 60 分） 一、 选择题：本大题共有 12 个小题，每小题 5 分，共 60 分.每小题给出的四个选项中，只 有一项是符合要求的． 1．复数 的虚部是 A． B．1 C． D． 2．已知全集 ， ， ，则图中阴影部分表示的集合是 A． B． C． D． 3．在 1，2，3，4，5，6，7 这组数据中，随机取出五个不同的数，则数 字 5 是取出的五个不同数的中位数的所有取法为 A．6 B．12 C．18 D．24 4．抛物线 C： 的焦点为 F， 为 C 上一点，过点 P 作其准线的垂线，垂足为 Q，若 ，则 的长度为 A． B． C． D． 5 ． 将 函 数 的 图 像 向 右 平 移 m 个 长 度 单 位 后 得 到 函 数 ， 若 与 的零点重合，则 m 的一个可能的值为 A． B． C． D． 1 2i 2 i + − i i− 1− U = R { | 1}M x x= < − { | ( 3) 0}N x x x= + < { | 3 1}x x− < < − { | 3 0}x x− < < { | 1 0}x x− <≤ { | 3}x x < − 2 4y x= P | | 3PF = | |FQ 2 2 3 2 3 4 2 ( ) sinf x x= ( )g x ( )g x ( ) cos( )3h x x π= + 3 π 6 π 2 3 π π 6．如图是 2017 年第一季度五省 GDP 情况图，则下列陈述中不正确的是 A．2017 年第一季度 GDP 总量和增速由高到低排位均居同一位的省只有 1 个 B．与去年同期相比，2017 年第一季度五个省的 GDP 总量均实现了增长 C．去年同期河南省的 GDP 总量不超过 4000 亿元 D．2017 年第一季度 GDP 增速由高到低排位第 5 的是浙江省 7．设 a，b 是两条不同的直线，α、β 是不重合的两个平面，则下列命题中正确的是 A．若 ， ，则 B．若 ， ，则 C．若 ， ，则 D．若 ， ， ，则 8．甲、乙、丙三人参加某公司的面试，最终只有一人能够被该公司录用， 得到面试结果以后，甲说：“丙被录用了”；乙说：“甲被录用了”；丙说： “我没被录用”．若这三人中仅有一人说法错误，则下列结论正确的是 A．甲被录用了 B．乙被录用了 C．丙被录用了 D．无法确定谁被录用了 9．若正整数 除以正整数 后的余数为 ，则记为 ，例如 ．如图程序框图的算法源于我国古代闻名中外的《中国剩 余定理》．执行该程序框图，则输出的 等于 A．20 B．21 C．22 D．23 10．一个几何体的三视图及尺寸如图所示，则该几何体的外接球的表面积为 A． B． C． D． 11．双曲线 的左右焦点分别为 、 ，点 P 是双曲 线右支上一点，若双曲线的一条渐近线垂直平分 ，则该双曲线的离心 率是 A． B． C．2 D． 12 ．已知函数 ， （e 是自然对数的底数），若关 于 x 的方程 恰有两个不等实根 、 ，且 ，则 的最小值为 A． B． C． D． a b⊥ a α⊥ //b α //a α α β⊥ //a β //a α //a β //α β //a b a α⊥ b β⊥ //α β N m n ( )modN n m= ( )10 2 mod4= n 24π 48π 96π 384π 2 2 2 2 1( 0, 0)x y a ba b − = > > 1F 2F 1PF 2 5 5 2 , 0( ) e ,x x xf x x >=   ≤0 ( ) exg x = ( ( )) 0g f x m− = 1x 2x 1 2x x< 2 1x x− 1 (1 ln 2)2 − 1 ln 22 + 1 ln 2− 1 (1 ln 2)2 + 第 II 卷 （非选择题　共 90 分） 注意事项： (1)非选择题的答案必须用 0.5 毫米黑色签字笔直接答在答题卡上，作图题可先用铅笔绘 出，确认后再用 0.5 毫米黑色签字笔描清楚，答在试题卷和草稿纸上无效. (2)本部分共 10 个小题，共 90 分. 二、填空题：本大题共 4 个小题，每小题 5 分，共 20 分． 13．已知变量 满足约束条件 ，则 的最大值为 ． 14．二项式 展开式中的常数项是 （用数字做答）． 15．已知函数 ，若 ，则实数 a 的取值范围是 ． 16．如图，在 中，角 的对边分别为 ， . 若 ， 为 外一点， ， ，则四边形 面 积的最大值为 ． 三、解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21 题为必考题， 每个试题考生都必须作答。第 22、23 题为选考题，考生根据要求作答。 （一）必考题：共 60 分。 17．（本小题满分 12 分） 已知数列 的前 项和为 满足 ． （Ⅰ）求数列 的通项公式； （Ⅱ）求数列 的前 项的和 ． 18．（本小题满分 12 分） 某企业库存有某批产品若干件，现从中随机抽取该种产品 500 件，测量出了这些产品的 质量指标值，由测量数据经整理获得如下统计表（质量指标值满分为 135）： 质量指标值 X 频数 Y 10 45 110 165 120 40 10 已知该批产品的质量指标值 ，其中 近似为样本的平均数， 近似为样 本方差 （同一组数据用该区间的中点值作代表）. （Ⅰ）求 的值； （Ⅱ）当产品的质量指标值 时，称该产品为一等品.某商家面向全社会招标采 购该类产品，期望所购买的该类产品中一等品的件数不得低于 10℅，以此期望为决策依据， 试问该企业的该类产品是否可以参与该商家的招标采购？请说明理由. 参考数据： ≈12.2. 若 ， 则 ， ， . x y， 0 2 2 0 0 x y x y x y + ≥  − + ≥  − ≤ 2z x y= − 8 3 1( )x x − ( ) sinf x x x= − 2( 2) ( )f a f a− + ≥0 ABC△ , ,A B C , ,a b c (sin cos )a b C C= + 2A π= D ABC△ 2DB = 1DC = ABDC { }na n nS *2 1( )n nS a n= − ∈N { }na *( 1) 1 3( )2 n n nb a n − += + ∈N 2n 2nT [65,75) [75,85) [85,95) [95,105) [105,115) [115,125) [125,135] 2( , )X N µ σ µ 2σ 2s (112.2 124.4)P X< ≤ 124.4X ≥ 150 2( , )Z N µ σ ( ) 0.6826P Zµ σ µ σ− < ≤ + = ( 2P Zµ σ− < ≤ 2 ) 0.9544µ σ+ = ( 3 3 ) 0.9974P Zµ σ µ σ− < ≤ + = 19．（本小题满分 12 分） 如图，三棱锥 的侧面 是等腰直角三角形， ， ， ，且 ． （I）求证：平面 平面 ； （II）求二面角 的余弦值． 20．（本小题满分 12 分） 已知椭圆 的左、右焦点分别为 ，若 到过椭圆左焦点、 斜率为 的直线的距离为 ，连接椭圆的四个顶点得到的四边形面积为 4． （I）求椭圆 C 的方程； （II）设椭圆 C 的左、右顶点分别为 A、B，过点 的直线 l 与椭圆 C 相交于 P、Q 两点，证明：直线 、 的交点在直线 上． 21．（本小题满分 12 分） 已知函数 ． （I）若 在 上恒成立，求正数 a 的取值范围； （II）证明： . （二）选考题：共 10 分。请考生在第 22、23 题中任选一题作答，如果多做，则按所做的 第一题计分。 22．（本小题满分 10 分）选修 4-4：坐标系与参数方程 在直角坐标系 xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，已知直线 l 的极坐标方程为 ， 的极坐标方程为 ． （I）求直线 l 和 的普通方程； （II）直线 l 与 有两个公共点 A、B，定点 P ，求 的值． 23．（本小题满分 10 分）选修 4-5：不等式选讲 设函数 ． A BCD− ABD△ 90BAD∠ =  BD DC= 120BDC∠ =  2AC AB= ABD ⊥ BCD B AC D− − ( )2 2 2 2: 1 0x yC a b a b + = > > 1 2,F F 2F 3 3 (1,0)M AP BQ 4x = 1( )= 1 2 lnaf x ax a xx −+ + − − ( ) 0f x ≥ [1, )x ∈ +∞ 1 1 11+ + + + ln( 1) )2 3 2( 1) nn nn n > + + ∈+ *N （ 3 cos sin 3 0ρ θ ρ θ+ − = C 4sin( )6 πρ θ= − C C (2, 3)− || | | ||PA PB− ( ) 1 , ( ) 2f x x g x x a= − = + D CB A （I）当 时，求不等式 的解集； （II）若关于 x 的不等式 有解，求 的取值范围． 泸州市高 2015 级（2018 届）第二次教学质量诊断性考试 数 学（理科）参考答案及评分意见 评分说明： 1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题 的主要考查内容比照评分参考制订相应的评分细则． 2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的 内容和难度．可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的 一半；如果后继部分的解答有较严重的错误，就不再给分． 3．解答右侧所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数，选择题和填空题不给中间分． 一、选择题 二、填空题 13．2； 14．28； 15. ； 16． . 三、解答题 17．解：（Ⅰ）当 时， ， 所以 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 因为 ， ， 所以 时， ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 两式相减得： ，即 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 因为 ，所以数列 是以 1 为首项，2 为公比的等比数列，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 所以 ；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 （Ⅱ）由 可知， 1a = a 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B C A C B A D A C C B D ( ) ( ) 1f x g x− > 22 ( ) ( ) ( 1)f x g x a+ +≤ ( , 2] [1, )−∞ − +∞ 5 24 + 1n = 1 12 1a a= − 1 1a = 2 1n nS a= − *n∈N 2n≥ 1 12 1n nS a− −= − 12 2n n na a a −= − 12n na a −= 1 0a ≠ { }na 12 ( )n na n− ∗= ∈N ( 1) 1 32 n n nb a − += + 当 为奇数时， ；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 当 为偶数时 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 则 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 分 .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 分 18．解： (Ⅰ) 由题得各组频率如下： 0.02， 0.09， 0.22， 0.33， 0.24， 0.08， 0.02 所以，抽取产品质量指标值的样本平均数 和样本方差 分别为 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 所以，由题得 ， 从而 ；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 （Ⅱ）因一件产品中一等品的概率为 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 设商家欲购产品的件数为 m,且其中一等品可能的件数为 ， 所以 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 所以 m 件产品中一等品的期望 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 分 又因商家欲购 m 产品中一等品的期望为 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11 分 因 ， 所以该批产品不能达到商家要求，不能参与招标. ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 分 19．证明：（I）如图，取 BD 中点 E，连结 、 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 因为 是等腰直角三角形， 所以 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 设 ，则 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 在 中，由余弦定理得： ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 因为 ， ， 所以 ，即 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 x 2s n 3nb = n 3n nb a= + 2 1 3 2 1 2 4 2( ) ( )n n nT b b b b b b−= + + + + + + +  1 3 2 13 (2 2 2 3 )nn n−= + + + + + 2 12(1 4 ) 2 26 61 4 3 3 n n n n +−= + = + −− [65,75) [75,85) [85,95) [95,105) [105,115) [115,125] [125,135) 70 0.02 80 0.09 90 0.22 100 0.33 110 0.24 120 0.08 130 0.02x = × + × + × + × + × + × + × 100= 2 2 2 2 2( 30) 0.02 ( 20) 0.09 ( 10) 0.22 0 0.33 10 0.24s = − × + − × + − × + × + × 2 220 0.08 30 0.02+ × + × 150= (100,150)X N 0.9544 0.6826(112.2 124.4) 0.13592P X −< ≤ = = ( 124.4) 0.5 0.4772 0.0228P X ≥ = − = ξ ( ,0.0228)B mξ  0.0228E mξ = 10 0.1m m=℅ 0.1E mξ < AE CE ABD△ AE BD⊥ AB a= 2BD CD a= = CDE△ 2 2 22 2( ) ( 2 ) 2 2 cos1202 2CE a a a a= + − ⋅ ⋅  27 2 a= 2 2AC AB a= = 2 2AE a= 2 2 2AC AE CE= + AE CE⊥ 又 ， ， 所以 平面 ， 所以平面 平面 ；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 （II）解法一：过点 E 在平面 内作 交 于点 F，由（I）知 平面 ， 分别以 为 x 轴，y 轴，z 轴建立如图空间直角坐标系，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 不妨设 ， 则： ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 则 ， ， ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 设平面 的法向量 ， 则 ，取 ， ∙∙∙∙∙∙∙∙∙10 分 设平面 的法向量 ， 则 ，取 ，∙∙∙∙∙11 分 所以 ， 因为二面角 的平面角是锐角， 所以二面角 的余弦值为 .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 分 解法二：过点 D 作 DN⊥AC 于点 N， 设 D 在平面 ABC 上的射影为 M，连接 MN， 则 AC⊥MN，所以∠DNM 为所求二面角的平面角，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 设 AB=1,则 AD=1,BD=CD= ，AC=2，BC= , 在△ADC 中，cos∠DAC= , 所以 DN= ,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 在△ABC 中，cos∠BAC= ,所以 sin∠BAC= , ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 由 , 所以 , 即 ,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11 分 AE BD⊥ BD CE E= AE ⊥ BCD ABD ⊥ BCD BCD EF BD⊥ BC AE ⊥ BCD , ,EB EF EA 2BD = (0,0,1), (1,0,0), ( 1,0,0), ( 2, 3,0)A B D C− − ( 2, 3, 1)AC = − − (1,0, 1)AB = − (1, 3,0)CD = − ABC ( , , )x y z=m 0 2 3 0 x z x y z − = − + = (1, 3,1)=m ABC ( , , )x y z=n 3 0 2 3 0 x y x y z  − = − + = ( 3,1, 3)= −n 3 105cos | || | 355 7 < >= = = ⋅ m nm,n m n B AC D− − B AC D− − 105 35 2 6 3 4 7 4 1 4 − 15 4 D ABC A BCDV V− −= 21 1 15 1 1 3 21 2 ( 2)3 2 4 3 2 2 2DM× × × × × = × × × × 10 5DM = 在△DMN 中，sin∠DNM= , 所以 cos∠DNM= , 所以二面角 的余弦值为 .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 分 20．解：（Ⅰ） 的坐标分别为 ， ， 其中 ， 过椭圆的左焦点、斜率为 的直线的方程为： ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 到直线 的距离为 3，所以有 ， 解得 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 所以有 ， 由题意知: ， 即 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 解得： ， ， 所求椭圆 C 的方程为 ； ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 （Ⅱ）设直线 l 的方程为 ，代入椭圆 C 的方程消去 x 整理得： ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 设 ， ， 所以 ， ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 直线 方程为 ，直线 方程为 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 解法一：要证明直线 、 的交点在直线 上， 只需证明 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 即证明 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 只需证明 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 分 即证明 ，而 成立， 所以直线 、 的交点在直线 上．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 分 解法二： ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 解得： ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 因为 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 分 4 2 35 105 35 B AC D− − 105 35 1 2,F F ( 0)c− ， ( 0)c， 0c> 3 3( )y x c= + 2F AB 2 3 3 3 1 c = + 3c = 2 2 3a b− = 1 2 2 42 a b× × = 2ab = 2a = 1b = 2 2 4 1x y+ = 1x my= + 2 2(4 ) 2 3 0m y my+ + − = 1 1( , )P x y 2 2( , )Q x y 1 2 2 2 4 my y m −+ = + 1 2 2 3 4 y y m −= + AP 1 1 ( 2)2 yy xx = ++ BQ 2 2 ( 2)2 yy xx = −− AP BQ 4x = 1 2 1 2 (4 2) (4 2)2 2 y y x x + = −+ − 2 1 1 2 1 23 6 2 0x y x y y y− − − = 2 1 1 2 1 23( 1) ( 1) 6 2 0my y my y y y+ − + − − = 1 2 1 22 3( ) 0my y y y− + = 2 22 33 2 4 4 0mm m m − −⋅ ⋅ + − = + AP BQ 4x = 1 2 1 2 ( 2) ( 2)2 2 y yx xx x + = −+ − 1 2 1 2 1 2 4 2 6 3 my y y yx y y − += + 1 2 1 2 2 3 y y m y y + = 即 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11 分 所以 . ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 分 21. 解：（Ⅰ）因为 ， ，则 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 . ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2 分 ①当 ，时，此时 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分 当 ，则 ， 在 上是减函数，所以在 上存 在x0， 使得 ， 在 上不恒成立； ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 ②当 时， ， 在 上成立， 在 上是增函数， ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分 在 上恒成立， 综上所述，所求a的取值范围为 ；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 （Ⅱ）由（Ⅰ）知当 时， 在 上恒成立， ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 令 ，有 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 当 时， ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 令 ，有 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 即 ， ， 将上述n个不等式依次相加得： ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分 整理得 . ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 1[1, )a a − 1(1, )a a − 0( ) (1) 0f x f< < 1 2 1 22 3( )my y y y= + 1 2 1 2 1 2 4 2 6 3 my y y yx y y − += + 12 2 1 1 2 26 6( ) 43 y y y y y y − += =+ + 1( )= 1 2 lnaf x ax a xx −+ + − − [1, )x ∈ +∞ (1)=0f 2 2 2 2 1 1 ( 1) 1( )= ( 1)( )a ax x a a af x a x xx ax x x − − − − −′ − − = = − − 10 2a< < 1 1a a − > 11 ax a −< < ( ) 0f x′ < ( )f x ( )f x ≥0 [1, )+∞ 1 2a≥ 1 1a a − ≤ ( ) 0f x′ ≥ [1, )+∞ ( )f x [1, )+∞ ( ) (1) 0f x f =≥ ( )f x ≥0 [1, )+∞ 1[ , )2 +∞ 1 2a≥ ( )f x ≥0 [1, )+∞ 1 1 2 ln 0( 1)aax a x xx −+ + − − ≥ ≥ 1 2a = 1 1( ) ln2 x xx − ≥ 1x > 1 1( ) ln2 x xx − > 1kx k += 1 1 1 1 1 1ln ( ) [(1 ) (1 )]2 1 2 1 k k k k k k k k + +< − = + − −+ + 1 1 1ln( 1) ln ( )2 1k k k k + − < + + 1,2,3, ,k n=  1 1 1 1 1ln( 1) ( + + + )2 2 3 2( 1)n n n + < + + + 1 1 11+ + + + ln( 1) 1)2 3 2( 1) nn nn n > + + + （ ≥ 22．解：（I）直线 l 的普通方程为： ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 因为圆 的极坐标方程为 ， 所以 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3 分 所以圆 的普通方程 ；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 （II）直线 l： 的参数方程为： （t 为参数），∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 代入圆 的普通方程 消去 x、y 整理得： ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 则 ， ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分 .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 分 23．解：（I）当 时， ，即 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 分 即 或 或 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4 分 所以 或 ， 所以原不等式的解集为 ；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5 分 （II） ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分 因为不等式 有解， 所以 ，即 ， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分 所以 的取值范围是 ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 分 1a = a 3 3 0x y+ − = C 4sin( )6 πρ θ= − 2 3 14 ( sin cos )2 2 ρ ρ θ θ= − C 2 2 2 2 3 0x y x y+ + − = 3 3 0x y+ − = 12 2 33 2 x t y t  = −  = − + 2C 2 2 2 2 3 0x y x y+ + − = 2 9 17 0t t− + = 1| | | |PA t= 2| | | |PB t= 1 2 1 2|| | | || || | | || | |PA PB t t t t− = − = − 2 2 1( )t t= − 2 2 1 1 2( ) 4t t t t= + − 29 4 17= − × 13= ( ) ( ) 1f x g x− > 1 2 1 1x x− − + > 1 1 2( 1) 1 x x x − − + + + > ≤ 1 1 1 2( 1) 1 x x x − < − + − + > ≤ 1 1 2( 1) 1 x x x >  − − + > 2 1x− < −≤ 21 3x− < < − 2( 2, )3 − − 2 ( ) ( ) 2 1 2f x g x x x a+ = − + + 2 2 2 2x x a= − + + 2 2 2 2x x a− − −≥ |2 2|a += 22 ( ) ( ) ( 1)f x g x a+ +≤ 2|2 2| ( 1)a a+ +≤ | 1| 2a + ≥ ( , 3] [1, ) { 1}−∞ − +∞ − 