上海市17区县2013届高三(数学理科)分类汇编:专题一 函数
专题一 函数
2013年2月
(松江区2013届高三一模 理科)18.设是定义在R上的偶函数,对任意,都有且当时,.若在区间内关于的方程恰有3个不同的实数根,则实数的取值范围是
A. B. C. D.
18.D
(浦东新区2013届高三一模 理科)16.已知函数,若函数为奇函数,则实数为 ( )
(黄浦区2013届高三一模 理科)17.若是上的奇函数,且在上单调递增,则下列结论:①是
偶函数;②对任意的都有;③在上单调递增;
④在上单调递增.其中正确结论的个数为
A.1 B.2 C.3 D.4
17.B
(青浦区2013届高三一模)18.已知函数是定义在上的单调增函数且为奇函数,数列是等差数列,,则的值………………………………( A ).
.恒为正数 恒为负数 .恒为0 .可正可负
(浦东新区2013届高三一模 理科)18.定义域为的函数图象的两个端点为,向量,是图象上任意一点,其中. 若不等式恒成立,则称函数在上满足“范围线性近似”,其中最小的正实数称为该函数的线性近似阀值.下列定义在
上函数中,线性近似阀值最小的是 ( )
(松江区2013届高三一模 理科)11.给出四个函数:①,②,③,④,其中满足条件:对任意实数及任意正数,都有及的函数为 ▲ .(写出所有满足条件的函数的序号)11.③
(松江区2013届高三一模 理科)15.过点且与直线平行的直线方程是
A. B.
C. D.
15.D
(杨浦区2013届高三一模 理科)9. 下列函数:① , ②, ③ , ④
⑤中,既是偶函数,又是在区间上单调递减函数为 (写出符合要求的所有函数的序号). 9.③⑤;
((虹口区2013届高三一模)17、定义域为的函数有四
个单调区间,则实数满足( )
17、C;
(奉贤区2013届高三一模)18、定义域是一切实数的函数,其图像是连续不断的,且存在常数()使得
对任意实数都成立,则称是一个“—伴随函数”. 有下列关于“—伴随函数”的结论:①是常数函数中唯一一个“—伴随函数”;
②“—伴随函数”至少有一个零点.;③是一个“—伴随函数”;其中正确结论的个数是 ( )
A.1个; B.2个; C.3个; D.0个;
18.A
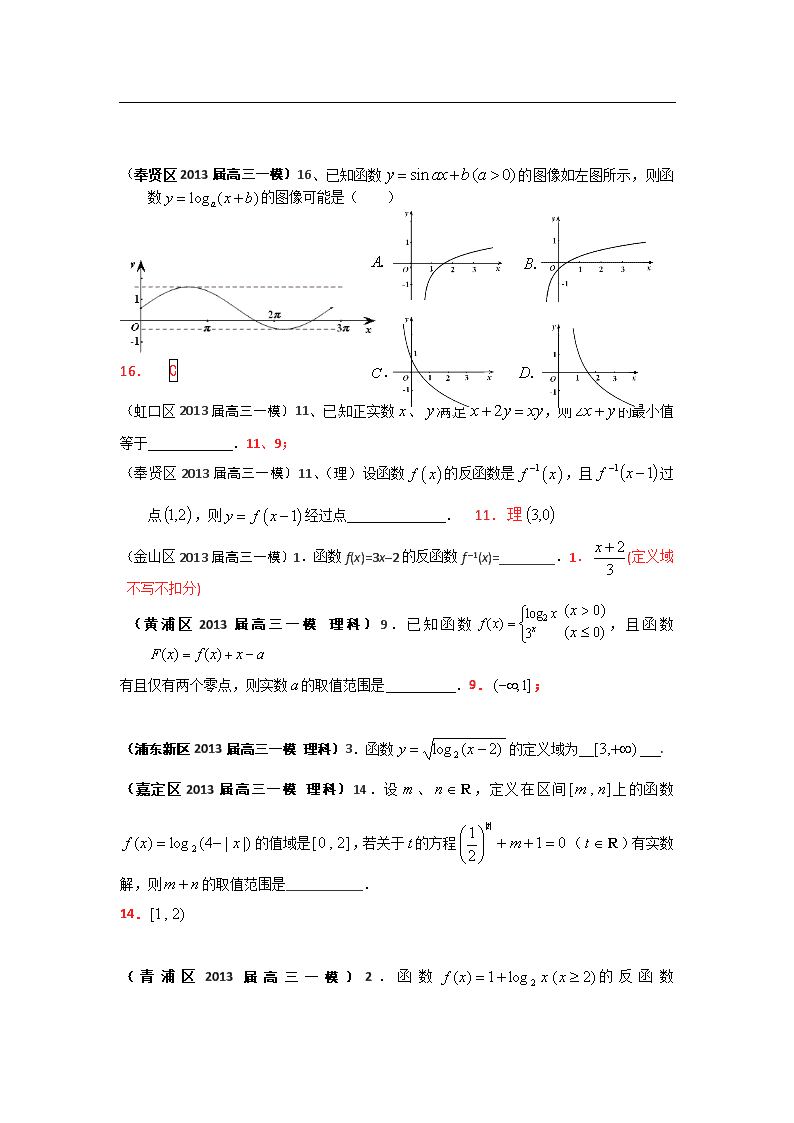
(奉贤区2013届高三一模)16、已知函数的图像如左图所示,则函数的图像可能是( )
[来源:Z*xx*k.Com]
16. C
(虹口区2013届高三一模)11、已知正实数、满足,则的最小值等于 .11、9;
(奉贤区2013届高三一模)11、(理)设函数的反函数是,且过点,则经过点 . 11.理
(金山区2013届高三一模)1.函数f(x)=3x–2的反函数f –1(x)=________.1.(定义域不写不扣分)
(黄浦区2013届高三一模 理科)9.已知函数,且函数
有且仅有两个零点,则实数的取值范围是 .9.;
(浦东新区2013届高三一模 理科)3.函数的定义域为 .
(嘉定区2013届高三一模 理科)14.设、,定义在区间上的函数的值域是,若关于的方程()有实数解,则的取值范围是___________.
14.
(青浦区2013届高三一模)2.函数的反函数
.
(松江区2013届高三一模 理科)3.若函数的图像与的图像关于直线对称,则= ▲ .3. 1
(奉贤区2013届高三一模)11、(文)若函数在区间内有零点,则实数a的取值范围是___.文
(浦东新区2013届高三一模 理科)5.函数()的反函数是 () .
(黄浦区2013届高三一模 理科)12.已知函数(且)满足,若是的反函数,
则关于x的不等式的解集是 .12.;
(金山区2013届高三一模)13.若函数y=f(x) (x∈R)满足:f(x+2)=f(x),且x∈[–1, 1]时,f(x) = | x |,函数y=g(x)是定义在R上的奇函数,且x∈(0, +∞)时,g(x) = log 3 x,则函数y=f(x)的图像与函数y=g(x)的图像的交点个数为_______. 13.4
(奉贤区2013届高三一模)7、设函数为奇函数,则 .7.
(嘉定区2013届高三一模 理科)18.设函数是定义在上以为周期的函数,若函数在区间上的值域为,则在区间上的值域为……………………( )
A. B. C. D.
18.D
(虹口区2013届高三一模)13、设定义在上的函数是最小正周期为
的偶函数,当时,,且在上单调递减,在上单调递增,则函数在上的零点个数为 . 13、20;
(杨浦区2013届高三一模 理科)1. 若函数的反函数为,则 .1. 0;
(奉贤区2013届高三一模)9、(理)已知函数那么的值为 .9.理
(青浦区2013届高三一模)12.已知满足对任意都有成立,那么的取值范围是_____ .
(奉贤区2013届高三一模)9、(文)已知函数 若,则_________. 文或
(崇明县2013届高三一模)5、已知是函数的反函数,则 . 5、
(宝山区2013届期末)7.将函数的图像按向量()平移,所得图像对应的函数为偶函数,则的最小值为 .
(崇明县2013届高三一模)14、已知,,若同时满足条件:①对于任意,
或成立; ②存在,使得成立.则的取值范围是
. 14、
(奉贤区2013届高三一模)1、关于的方程的一个根是,则_________.1.
(长宁区2013届高三一模)2、记函数的反函数为如果函数的图像过点,那么函数的图像过点 2、
(奉贤区2013届高三一模)5、已知且若恒成立,则实数m的取值范围是_________.5.
(宝山区2013届期末)8.设函数是定义在R上周期为3的奇函数,且,则 _.0
(长宁区2013届高三一模)5、设为定义在上的奇函数,当时,(为常数),
则 5、
(宝山区2013届期末)14.设是平面直角坐标系上的两点,定义点A到点B的曼哈顿距离. 若点A(-1,1),B在上,则的最小值为 .
(长宁区2013届高三一模)13、(理)已知函数的值域为,若关于的不等式的解集为,则实数的值为 13、(理) ,
(宝山区2013届期末)
18.已知则下列函数的图像错误的是……………………( D )
(A)的图像 (B)的图像 (C)的图像 (D)的图像
(崇明县2013届高三一模)15、设函数,则下列结论错误的是………………………………………( )
A.的值域为 B.是偶函数
C.不是周期函数 D.不是单调函数
15、
(长宁区2013届高三一模)18、(理)函数,的图象可能是下列图象中的 ( )
18、
(黄浦区2013届高三一模 理科)23.(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分7分,第3小题满分8分.
对于函数与常数,若恒成立,则称为函数的一个“P数对”;若恒成立,则称为函数的一个“类P数对”
.设函数的定义域为,且.
(1)若是的一个“P数对”,求;
(2)若是的一个“P数对”,且当时,求在区间上的最大值与最小值;
(3)若是增函数,且是的一个“类P数对”,试比较下列各组中两个式子的大小,并说明理由.
①与+2;②与. [来源:Zxxk.Com]
23.(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分7分,第3小题满分8分.
解:(1)由题意知恒成立,令,
可得,∴是公差为1的等差数列,
故,又,故. ………………………………3分
(2)当时,,令,可得,
解得,即时,, ………………………4分
故在上的取值范围是.
又是的一个“P数对”,故恒成立,
当时,,
…, …………………6分
故为奇数时,在上的取值范围是;
当为偶数时,在上的取值范围是. …………………8分
所以当时,在上的最大值为,最小值为3;
当为不小于3的奇数时,在上的最大值为,最小值为;
当为不小于2的偶数时,在上的最大值为,最小值为.………10分
(3)由是的一个“类P数对”,可知恒成立,
即恒成立,令,可得,
即对一切恒成立,[来源:Z+xx+k.Com]
所以…,
故. …………………………………14分
若,则必存在,使得,
由是增函数,故,
又,故有.…………………………………18分
(金山区2013届高三一模)21.(本题满分14分,第1小题6分,第2小题8分)
已知函数,其中常数a > 0.
(1) 当a = 4时,证明函数f(x)在上是减函数;
(2) 求函数f(x)的最小值.
21.解:(1) 当时,,…………………………………………1分
任取0
0,即f(x1)>f(x2)………………………………………5分
所以函数f(x)在上是减函数;………………………………………………………6分
(2),……………………………………………………7分
当且仅当时等号成立,…………………………………………………………8分
当,即时,的最小值为,………………………10分
当,即时,在上单调递减,…………………………………11分
所以当时,取得最小值为,………………………………………………13分
综上所述: ………………………………………14分
(浦东新区2013届高三一模 理科)23.(本题满分18分,第1小题满分4分,第2小题满分4分,第3小题满分10分)
设函数
(1)求函数和的解析式;
(2)是否存在非负实数,使得恒成立,若存在,求出的值;若不存在,请说明理由;
(3)定义,且
① 当时,求的解析式;
已知下面正确的命题:当时,都有恒成立.
② 对于给定的正整数,若方程恰有个不同的实数根,确定的取值范围;
若将这些根从小到大排列组成数列,求数列所有项的和.
解:(1)函数
函数 ……4分
(2),……6分
当时,则有恒成立.
当时,当且仅当时有恒成立.
综上可知当或时,恒成立;………………………8分
(3)① 当时,对于任意的正整数,都有
故有…13分
② 由①可知当时,有,根据命题的结论可得,
当时,有,
故有.
因此同理归纳得到,当时,
……………………15分
对于给定的正整数,时,
解方程得,,
要使方程在上恰有个不同的实数根,
对于任意,必须恒成立,
解得, 若将这些根从小到大排列组成数列,
由此可得 .……………………17分
故数列所有项的和为:
.……18分
(长宁区2013届高三一模)19、(本题满分12分)已知,满足.
(1)将表示为的函数,并求的最小正周期;
(2)(理)已知分别为的三个内角对应的边长,若,且,求的取值范围.
19、解(1)由得 …………3分
即
所以,其最小正周期为. …………6分
(2)(理)因为,则
.因为为三角形内角,所以…………9分
法一:由正弦定理得,,
,,,
所以的取值范围为 …………12分
法二:,因此,
因为,所以,,
.又,所以的取值范围为 …………12分
(文)(2),因此的最小值为,…………9分
由恒成立,得,
所以实数的取值范围是. ………12分
(宝山区2013届期末)21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数,.
(1)当时,求的定义域;
(2)若恒成立,求的取值范围.
解:(1)由………………………………………………3分
解得的定义域为.………………………6分
(2)由得,即……………………9分
令,则,………………………………………………12分
当时,恒成立.………………………………………………14分
(长宁区2013届高三一模)22. (本小题满分18分) (理)已知函数 。
(1)求函数的定义域和值域;
(2)设(为实数),求在时的最大值;
(3)对(2)中,若对所有的实数及恒成立,求实数的取值范围。
(文)已知二次函数。
(1)函数在上单调递增,求实数的取值范围;
(2)关于的不等式在上恒成立,求实数的取值范围;
(3)函数在上是增函数,求实数的取值范围。
22、(理)解:由1+x≥0且1-x≥0,得-1≤x≤1,所以定义域为 …………2分
又由≥0 得值域为 …………4分
(2)因为
令,则,
∴()+t= …………6分
由题意知g(a)即为函数的最大值。
注意到直线是抛物线的对称轴。…………7分
因为a<0时,函数y=m(t), 的图象是开口向下的抛物线的一段,
①若,即则 …………8分
②若,即则…………10分
③若,即则 …………11分
综上有 …………12分
(3)易得, …………14分
由对恒成立,
即要使恒成立,…………15分
,令,对所有的成立,
只需 …………17分
求出m的取值范围是. …………18分
(文)解:(1)当时,,不合题意;……………1分
当时,在上不可能单调递增;……………2分
当时,图像对称轴为,
由条件得,得 ……………4分
(2)设, ……………5分
当时,, ……………7分
因为不等式在上恒成立,所以在时的最小值大于或等于2,
所以, , ……………9分
解得。 ……………10分
(3)在上是增函数,设,则,
,,……………12分
因为,所以, ……………14分
而, ……………16分
所以 ……………18分
(崇明县2013届高三一模)22、(本题16分,第(1)小题4分;第(2)小题6分;第(3)小题6分)
设函数.
(1)当时,求函数在区间内的零点;
(2)设,证明:在区间内存在唯一的零点;
(3)设,若对任意,有,求的取值范围.
22、解:(1),令,得,
所以。
(2)证明:因为 ,。所以。所以在内存在零点。
,所以在内单调递增,所以在内存在唯一零点。
(3)当n=2时,f2(x)=x2+bx+c.
对任意x1,x2∈[-1,1]都有|f2(x1)-f2(x2)|≤4等价于f2(x)在[-1,1]上的最大值与最小值之差M≤4.
据此分类讨论如下:
①当,即|b|>2时,M=|f2(1)-f2(-1)|=2|b|>4,与题设矛盾。
②当-1≤<0,即0<b≤2时,M=f2(1)-f2()=(+1)2≤4恒成立.
③当0≤≤1,即-2≤b≤0时,M=f2(-1)-f2()=(-1)2≤4恒成立.
综上可知,-2≤b≤2.[来源:学&科&网Z&X&X&K]
注:②,③也可合并证明如下:
用max{a,b}表示a,b中的较大者.
当-1≤≤1,即-2≤b≤2时,M=max{f2(1),f2(-1)}-f2()
=
=1+c+|b|-(+c)
=(1+)2≤4恒成立.
(奉贤区2013届高三一模)23、(理)设函数
定义域为,且.
设点是函数图像上的任意一点,过点分别作直线和
轴的垂线,垂足分别为.
(1)写出的单调递减区间(不必证明);(4分)
(2)问:是否为定值?若是,则求出该定值,
若不是,则说明理由;(7分)
(3)设为坐标原点,求四边形面积的最小值.(7分)
23、解:(1)、因为函数的图象过点,
所以 2分
函数在上是减函数. 4分
(2)、(理)设 5分
直线的斜率
则的方程 6分
联立
9分
, 11分
(2)、(文)设 5分
直线的斜率为 6分
则的方程 7分
联立 8分
11分
3、 12分
13分
∴, 14分
, 15分
∴ , 16分
17分
当且仅当时,等号成立.
∴ 此时四边形面积有最小值. 18分
(奉贤区2013届高三一模)23、(文)设函数定义域为,且.
设点是函数图像上的任意一点,过点分别作直线和
轴的垂线,垂足分别为.
(1)写出的单调递减区间(不必证明);(4分)
(2)设点的横坐标,求点的坐标(用的代数式表示);(7分)
(3)设为坐标原点,求四边形面积的最小值.(7分)
23、解:(1)、因为函数的图象过点,
所以 2分
函数在上是减函数. 4分
(2)、(理)设 5分
直线的斜率
则的方程 6分
联立
9分
, 11分
(2)、(文)设 5分
直线的斜率为 6分
则的方程 7分
联立 8分
11分
3、 12分
13分
∴, 14分
, 15分
∴ , 16分
17分
当且仅当时,等号成立.
∴ 此时四边形面积有最小值. 18分
(虹口区2013届高三一模)23、(本题满分18分)如果函数的定义域为,对于定义域内的任意,存在实数使得成立,则称此函数具有“性质”.
(1)判断函数是否具有“性质”,若具有“性质”求出所有的值;若不具有“性质”,请说明理由.
(2)已知具有“性质”,且当时,求在上的最大值.
(3)设函数具有“性质”,且当时,.若与交点个数为2013个,求的值.
23、(18分)解:(1)由得,根据诱导公式得.具有“性质”,其中.
………………4分
(2)具有“性质”,.
设,则,
……………………6分
当时,在递增,时
当时,在上递减,在上递增,且, 时[来源:Zxxk.Com]
当时,在上递减,在上递增,且,时
综上所述:当时, ;当时,
………………………………11分
(3)具有“性质”,,,
,从而得到是以2为周期的函数.[来源:学,科,网Z,X,X,K]
又设,则,
.
再设(),
当(),则,
;
当(),则,;
对于,(),都有,而,,是周期为1的函数.
①当时,要使得与有2013个交点,只要与在
有2012个交点,而在有一个交点.过,从而得
②当时,同理可得
③当时,不合题意.
综上所述…………………………18分
(青浦区2013届高三一模)23.(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
我们把定义在上,且满足(其中常数满足)的函数叫做似周期函数.
(1)若某个似周期函数满足且图像关于直线对称.求证:函数是偶函数;
(2)当时,某个似周期函数在时的解析式为,求函数,的解析式;
(3)对于确定的时,,试研究似周期函数函数在区间上是否可能是单调函数?若可能,求出的取值范围;若不可能,请说明理由.
解:因为关于原点对称,……………………………………………………1分
又函数的图像关于直线对称,所以
① ………………………………………………………2分
又,
用代替得③ ……………………………………………3分
由①②③可知,
.即函数是偶函数;…………………………………………4分
(2)当时,
;……10分
(3)当时,
…………………12分
显然时,函数在区间上不是单调函数 …………………13分
又时,是增函数,
此时……………………………………14分
若函数在区间上是单调函数,那么它必须是增函数,则必有
, ………………………………………………………16分
解得 . ………………………………………………………18分
(嘉定区2013届高三一模 理科)23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设,函数.
(1)若,求函数在区间上的最大值;
(2)若,写出函数的单调区间(不必证明);
(3)若存在,使得关于的方程有三个不相等的实数解,求实数的取值范围.
23.(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
(1)当,时,…(2分)
作函数图像(图像略),可知函数在区间上是增函数,所以的最大值为.…………(4分)
O
a
y
x
(2)……(1分)
①当时,,
因为,所以,
所以在上单调递增.…………(3分)
②当时,,
因为,所以,所以在上单调递增,在上单调递减.…………(5分)
综上,函数的单调递增区间是和,
单调递减区间是.………………(6分)
(3)①当时,,,所以在上是增函数,关于的方程不可能有三个不相等的实数解.…………(2分)
②当时,由(1)知在和上分别是增函数,在上是减函数,当且仅当时,方程有三个不相等的实数解.
即.…………(5分)
令,在时是增函数,故.…………(7分)
所以,实数的取值范围是.…………(8分)
(杨浦区2013届高三一模 理科)22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知函数的值域为集合,
(1)若全集,求;
(2)对任意,不等式恒成立,求实数的范围;
(3)设是函数的图像上任意一点,过点分别向直线和轴作垂线,垂足分别为、,求的值.
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
(1)由已知得, ,则 ………1分
当且仅当时,即等号成立,
………3分
所以, ………4分
(2)由题得 ………5分
函数在的最大值为 ………9分
………10分
(3)设,则直线的方程为,
即, ………11分
由 得 ………13分
又, ………14分
所以,,故 ………16分