2018-2019学年山西省长治二中高二上学期第二次月考数学（理）试题 B卷（Word版）

2018-2019学年山西省长治二中高二上学期第二次月考数学（理）试题 B卷（Word版）

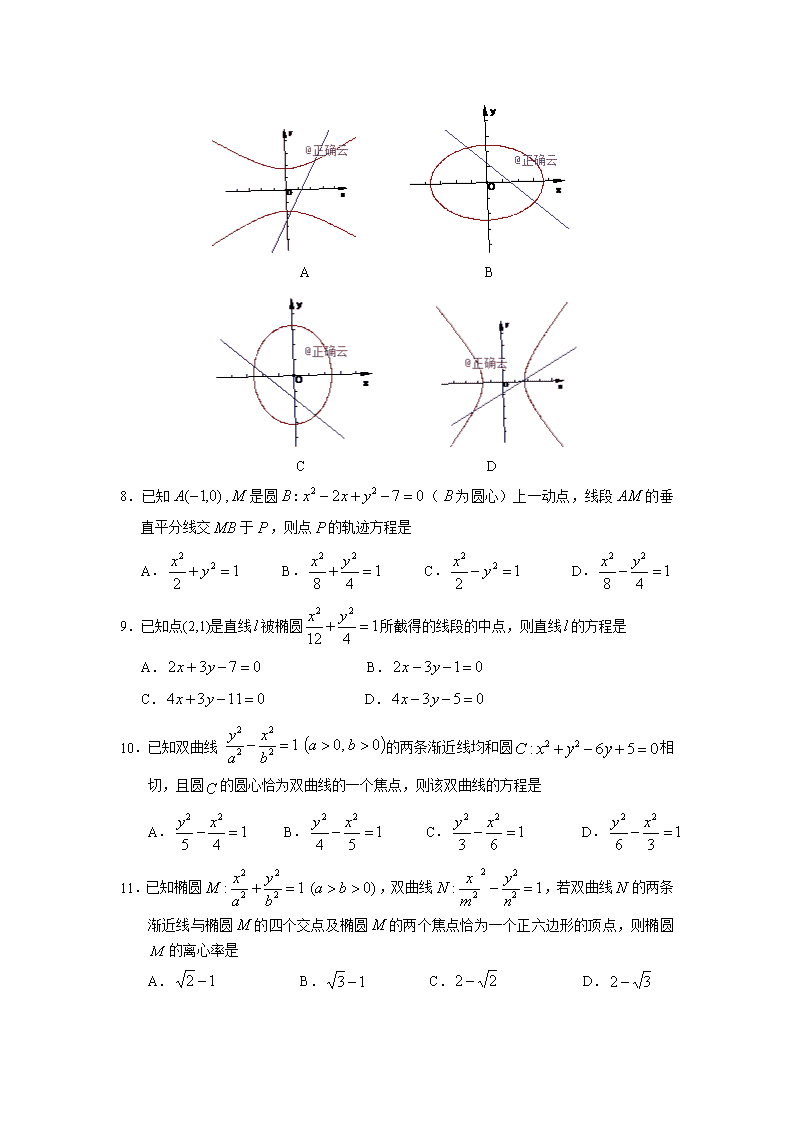
‎2018-2019学年山西省长治二中高二上学期第二次月考数学（理）试题 B卷 命题人：原晓琴 审题人：王宏伟 ‎【本试卷满分150分，考试时间为120分钟】‎ 一、选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．已知双曲线的标准方程是 其渐近线方程是 A． B． C． D．‎ ‎2．设是两条不同的直线，为两个不同的平面，则下列命题正确的是 A．若，则 B．若，则 ‎ C．若，则 D．若，则 ‎ ‎3．以双曲线的焦点为顶点，顶点为焦点的椭圆方程是 A． B． C． D．‎ ‎4．已知点在圆内，则直线与圆的位置关系是 A．相切 B．相离 C．相交 D．不确定 ‎5．若椭圆的离心率为，则双曲线的离心率为 A． B． C． D．‎ ‎6．若圆上恰有2个点到直线的距离等于1，则的取值范围是 A． B． ‎ C． D．‎ ‎7．设那么直线和曲线的图象可以是 ‎ ‎ A B ‎ ‎ C D ‎8．已知,是圆（为圆心）上一动点，线段的垂直平分线交于，则点的轨迹方程是 A． B． C． D．‎ ‎9．已知点(2,1)是直线被椭圆所截得的线段的中点，则直线的方程是 A． B．‎ C． D．‎ ‎10．已知双曲线的两条渐近线均和圆相切，且圆的圆心恰为双曲线的一个焦点，则该双曲线的方程是 A． B． C． D．‎ ‎11．已知椭圆，双曲线，若双曲线的两条渐近线与椭圆的四个交点及椭圆的两个焦点恰为一个正六边形的顶点，则椭圆的离心率是 A． B． C． D．‎ ‎12．已知双曲线是实轴端点，是右焦点，是虚轴端点，若在线段上（不含端点）存在不同的两点，使得构成以为斜边的直角三角形，则双曲线离心率的取值范围是 A． B． C． D．‎ 二、填空题：本大题共4小题，每小题5分，共20分.把答案填在答卷的相应位置 ‎13．椭圆的焦点坐标是　　　．‎ ‎14．过点引直线，使点，到它的距离相等，则所求直线方程是　　　　．(写出直线的一般式方程）‎ ‎15．在长方体中，,,则与平面所成角的正弦值是　　　　.‎ ‎16．已知实数满足，则最大值是　　　　．‎ 三、解答题:本大题共70分 ‎17．(本题满10分)已知双曲线的焦点坐标为,实轴长为4‎ ‎（1）求双曲线标准方程；‎ ‎（2）若双曲线上存在一点使得，求的面积.‎ ‎18．(本题满分12分)已知点,圆(为坐标原点）‎ ‎（1）求经过,以及圆与圆交点的圆的方程;‎ ‎（2）过点向圆引两条切线,切点分别为,求直线的方程.‎ ‎19．(本题满分12分)如图，边长为3的等边三角形ABC，E,F分别在边AB,AC上,且AE=AF=2,M为BC边的中点，AM交EF于点O,沿EF将,折到DEF的位置，使 ‎（1）证明;‎ ‎（2）在BC边上是否存在点N，使得二面角D-EN-F为，若存在，求出的值，若不存在，说明理由.‎ ‎20．(本题满分12分)已知的一个顶点是,的平分线在直线上,边上的中线在直线上.求 ‎（1）顶点的坐标;‎ ‎（2）直线BC的方程．‎ ‎21．(本题满分12分) 已知椭圆的两个焦点坐标分别是,并且经过点（，），圆的直径为(为坐标原点）‎ ‎（1）求椭圆的标准方程；‎ ‎（2）设直线与圆相切于第一象限内的点 ‎①若直线与椭圆有且只有一个公共点，求点的坐标；‎ ‎②直线与椭圆交于两点，若的面积为，求直线的方程.‎ ‎22．（本题满分12分） 在平面直角坐标系xOy中，点与定点的距离和它到直线的距离的比是常数 ‎（1）求点的轨迹方程；‎ ‎（2）设过点的直线与曲线交于点(不在轴上），垂直于的直线与交于点，与轴交于点,若,且,求直线斜率的取值范围.‎ ‎-2019学年第一学期高二第二次月考数学参考答案（理）‎ ‎1---12ACDBB BDAAA BB ‎ ‎13. 14. ‎ ‎15. 16. ‎ ‎17 解:(1) 由条件 双曲线方程为...................................5分 ‎(2). 由双曲线定义 ‎..............................10分 18. 解: (1)设圆的方程为, 因为点在圆上，‎ 所以，所求圆的方程是......................6分 ‎（2）以MO为直径的圆的方程为 所以直线AB方程是................................................12分 ‎19 解:(1) 在中，‎ 由得 ‎.............6分 (2) ‎.由（1）以O为原点OE,OM,OD分别为x轴，y轴，z轴建立空间直角坐标系，则E(1，0，0) D B ，M 设,则,‎ 设平面DEN的法向量为，则 取,又平面EFCB的法向量取 由条件,，所以 即存在点N，且.,使得.二面角D-EN-F为........................12分 ‎20 解:(1).设C(a,b),则b=3a ‎ 又AC的中点M在AC边的中线上，‎ 所以由，解之........................6‎ （2） 设A点关于直线对称点的坐标是（m,n)‎ 则，解之 直线BC方程为.......................................................12分 ‎21（1）由条件 解之椭圆标准方程........................................3分 ‎(2) 设直线的方程为 ‎ 圆O的方程为，直线与圆相切，则 所以，解方程组 ①‎ 化简得 ‎.‎ ‎①当直线与椭圆只有一个公共点 直线的方程为，方程组的解为所以P........7分 ‎②直线与椭圆交于两点,设，则，‎ 又，‎ ‎，解之 当时,直线与椭圆有两个不同的交点.‎ 直线AB的方程为.............................12分 ‎22.解:(1) 由条件得，化简可得 所以椭圆方程为..............................3分 ‎(2).设直线的方程为，设B 联立 整理得 解得 或， 从而 ‎ 由（1）知，F(1，0),设, 由得 所以解得 因此直线DP的方程为设由方程组 得 在中，,即 化简得,即，解得或，‎ 所以直线的斜率取值范围为.............................12分