数学文卷·2018届北京市朝阳区高三第一学期期末质量检测（2018

数学文卷·2018届北京市朝阳区高三第一学期期末质量检测（2018

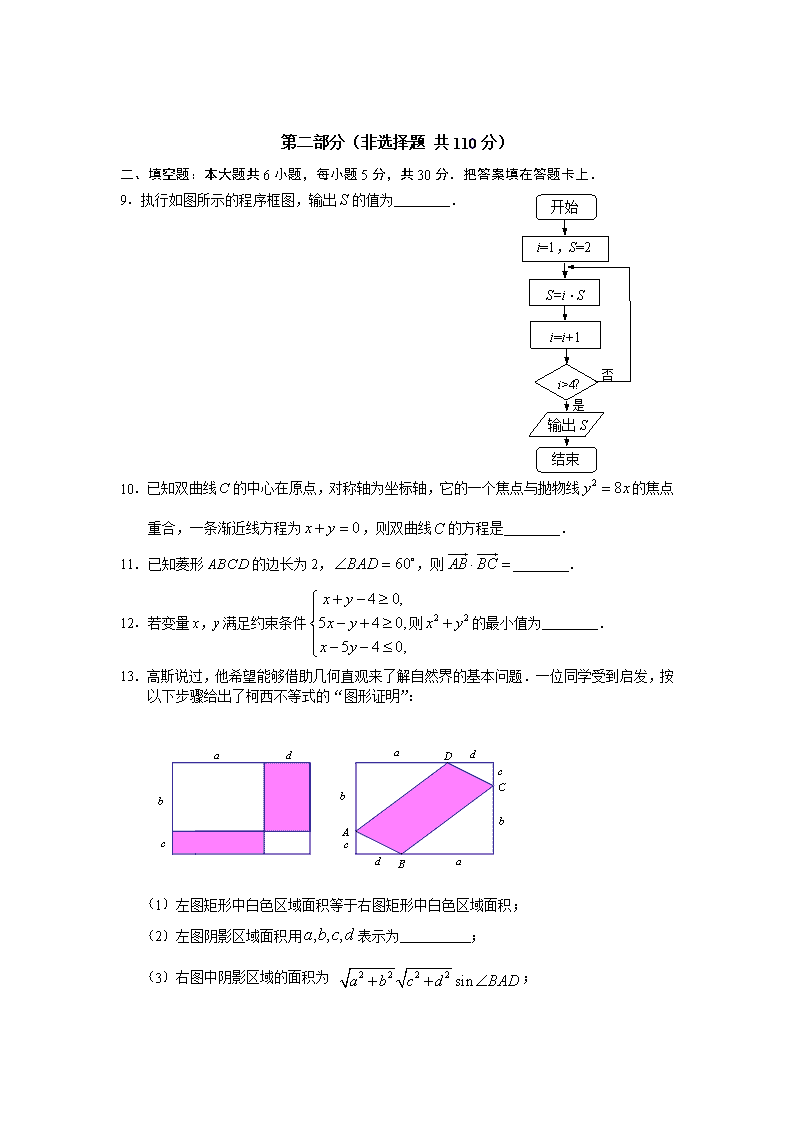
‎ 北京市朝阳区2017-2018学年度第一学期期末质量检测 ‎ 高三年级数学试卷（文史类） 2018．1‎ ‎（考试时间120分钟 满分150分）‎ 本试卷分为选择题（共40分）和非选择题（共110分）两部分 第一部分（选择题 共40分）‎ 一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．‎ 1. 已知集合，，则是 A． B． ‎ C． D． ‎ ‎2．已知为虚数单位，设复数满足，则=‎ A． B． C． D．‎ ‎3．某便利店记录了100天某商品的日需求量（单位：件），整理得下表：‎ 日需求量n ‎14‎ ‎15‎ ‎16‎ ‎18‎ ‎20‎ 频率 ‎0．1‎ ‎0．2‎ ‎0．3‎ ‎0．2‎ ‎0．2‎ 试估计该商品日平均需求量为 A． B． C． D． ‎ ‎4． “”是“”的 ‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎5． 下列函数中，是奇函数且在内是减函数的是 ‎① ② ③ ④‎ A．①③ B．①④ C．②③ D．③④‎ ‎6． 某四棱锥的三视图如图所示，格纸上小正方形的边长为1，则该四棱锥的体积为 A． B． ‎ C． D． ‎ ‎7．阿波罗尼斯（约公元前262-190年）证明过这样一个命题:平面内到两定点距离之比为常数（且）的点的轨迹是圆．后人将这个圆称为阿氏圆．若平面内两定点间的距离为2，动点与，距离之比为，当不共线时，面积的最大值是 A． B． C． D． ‎ ‎8．如图，为等边三角形，四边形为正方形，平面平面．若点为平面内的一个动点，且满足，则点在正方形及其内部的轨迹为 ‎ P A B D C M A．椭圆的一部分 ‎ B．双曲线的一部分 ‎ C．一段圆弧 ‎ D．一条线段 第二部分（非选择题 共110分）‎ 二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上． ‎ 开始 i=1，S=2‎ 结束 i=i+1‎ i>4?‎ 输出S 是 否 S=i·S ‎9．执行如图所示的程序框图，输出的值为 ．‎ ‎10．已知双曲线的中心在原点，对称轴为坐标轴，它的一个焦点与抛物线的焦点重合，一条渐近线方程为，则双曲线的方程是 ．‎ ‎11．已知菱形的边长为2，，则 ．‎ ‎12．若变量x，y满足约束条件则的最小值为 ．‎ ‎13．高斯说过，他希望能够借助几何直观来了解自然界的基本问题．一位同学受到启发，按以下步骤给出了柯西不等式的“图形证明”：‎ ‎（1）左图矩形中白色区域面积等于右图矩形中白色区域面积；‎ ‎（2）左图阴影区域面积用表示为 ； ‎ ‎（3）右图中阴影区域的面积为 ；‎ ‎（4）则柯西不等式用字母可以表示为．‎ 请简单表述由步骤（3）到步骤（4）的推导过程： ．‎ ‎14．如图，一位同学从处观测塔顶及旗杆顶，得仰角分别为和. 后退 (单位m)至点处再观测塔顶，仰角变为原来的一半，设塔和旗杆都垂直于地面，且，，三点在同一条水平线上，则塔的高为 m；旗杆的高为 m.（用含有和的式子表示）‎ 三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．‎ ‎15．（本小题满分13分）‎ 已知函数．‎ ‎（Ⅰ）求的最小正周期；‎ ‎（Ⅱ）求证：当时，．‎ ‎16．（本小题满分13分）‎ 已知由实数构成的等比数列满足，．‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）求．‎ ‎17．（本小题满分13分）‎ ‎2017年，世界乒乓球锦标赛在德国的杜赛尔多夫举行．整个比赛精彩纷呈，参赛选手展现出很高的竞技水平，为观众奉献了多场精彩对决．图1（扇形图）和表1是其中一场关键比赛的部分数据统计．两位选手在此次比赛中击球所使用的各项技术的比例统计如图1．在乒乓球比赛中，接发球技术是指回接对方发球时使用的各种方法．选手乙在比赛中的接发球技术统计如表1，其中的前4项技术统称反手技术，后3项技术统称为正手技术．‎ 图1‎ 选手乙的接发球技术统计表 技术 反手拧球 反手搓球 反手拉球 反手拨球 正手搓球 正手拉球 正手挑球 使用次数 ‎20‎ ‎2‎ ‎2‎ ‎4‎ ‎12‎ ‎4‎ ‎1‎ 得分率 ‎55%‎ ‎50%‎ ‎0%‎ ‎75%‎ ‎41．7%‎ ‎75%‎ ‎100%‎ 表1‎ ‎（Ⅰ）观察图1，在两位选手共同使用的8项技术中，差异最为显著的是哪两项技术？‎ ‎（Ⅱ）乒乓球接发球技术中的拉球技术包括正手拉球和反手拉球．从表1统计的选手乙的所有拉球中任取两次，至少抽出一次反手拉球的概率是多少？‎ ‎（Ⅲ）如果仅从表1中选手乙接发球得分率的稳定性来看（不考虑使用次数），你认为选手乙的反手技术更稳定还是正手技术更稳定？（结论不要求证明）‎ ‎18．（本小题满分14分）‎ A C B B1‎ C1‎ A1‎ D 如图，在三棱柱中，底面为正三角形，侧棱底面．已知是的中点，．‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求证：∥平面；‎ ‎（Ⅲ）求三棱锥的体积．‎ ‎19．（本小题满分14分）‎ 已知椭圆的一个焦点坐标为．‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）已知点，过点的直线（与轴不重合）与椭圆交于两点，直线与直线相交于点，试证明：直线与轴平行．‎ ‎20．（本小题满分13分）‎ 已知函数，．‎ ‎（Ⅰ）求曲线在点处的切线的斜率；‎ ‎（Ⅱ）判断方程（为的导数）在区间内的根的个数，说明理由；‎ ‎（Ⅲ）若函数在区间内有且只有一个极值点，求的取值范围．‎ 北京市朝阳区2017-2018学年度第一学期期末质量检测 ‎ 高三年级数学试卷答案（文史类） 2018.1‎ 一、选择题（40分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 C B D A A B A D 二、填空题（30分）‎ 题号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ 答案 ‎；两个要点：（1）两图中的阴影部分面积相等；‎ ‎（2）.‎ ‎;‎ 三、解答题（80分）‎ ‎15. （本小题满分13分）‎ 解：（Ⅰ）因为 ‎ ‎.‎ 所以函数的最小正周期为. …………………………7分 ‎（Ⅱ）由（Ⅰ）可知，．‎ 当时，，‎ ‎，‎ ‎.‎ 当即时，取得最小值．‎ 所以当时，. …………………………13分 ‎16. （本小题满分13分）‎ 解：（Ⅰ）由可得.‎ 由数列各项为实数，解得，.‎ 所以数列的通项公式为或. …………………7分 ‎（Ⅱ）当时，；‎ 当时，.…13分 ‎17. （本小题满分13分）‎ 解：（Ⅰ）根据所给扇形图的数据可知，差异最为显著的是正手搓球和反手拧球两项技术.‎ ‎ ………………2分 ‎（Ⅱ）根据表1的数据可知，选手乙的反手拉球2次，分别记为A,B,正手拉球4次，分别记为a,b,c,d.则从这六次拉球中任取两次，共15种结果，分别是:‎ AB, Aa,Ab, Ac, Ad, Ba, Bb，Bc, Bd, ab，ac, ad, bc, bd,cd.‎ 其中至少抽出一次反手拉球的共有9种，分别是:‎ AB,Aa，Ab，Ac, Ad, Ba, Bb，Bc, Bd.‎ 则从表1统计的选手乙的所有拉球中任取两次，至少抽出一次反手拉球的概率. …………………………10分 ‎（Ⅲ）正手技术更稳定. …………………………13分 ‎18. （本小题满分14分）‎ ‎（Ⅰ）证明：由已知为正三角形，且是的中点，‎ 所以．‎ ‎ 因为侧棱底面，，‎ 所以底面．‎ ‎ 又因为底面，所以.‎ ‎ 而,‎ 所以平面．‎ 因为平面，所以平面平面．…………………………5分 A C B B1‎ C1‎ A1‎ D E ‎（Ⅱ）证明：连接，设，连接．‎ 由已知得，四边形为正方形，则为的中点.‎ 因为是的中点，‎ 所以．‎ 又因为平面，‎ 平面，‎ 所以∥平面． …………………………10分 ‎（Ⅲ）由（Ⅱ）可知∥平面，‎ 所以与到平面的距离相等，‎ 所以．‎ 由题设及，得，且．‎ 所以，‎ 所以三棱锥的体积为． …………………………14分 ‎19. （本小题满分14分）‎ 解：（Ⅰ）由题意可知所以.‎ ‎ 所以椭圆的方程为. …………………………3分 ‎（Ⅱ）①当直线的斜率不存在时，此时轴.设，直线与 轴相交于点，易得点是点和点的中点，又因为，‎ ‎ 所以.‎ 所以直线轴.‎ ‎②当直线的斜率存在时，设直线的方程为，‎ ‎.‎ ‎ 因为点，所以直线的方程为.‎ ‎ 令，所以.‎ ‎ 由消去得.‎ ‎ 显然恒成立.‎ ‎ 所以 ‎ 因为 ‎ ‎ ‎，‎ ‎ 所以.‎ 所以直线轴.‎ 综上所述，所以直线轴. …………………………14分 ‎20. （本小题满分13分）‎ 解：（Ⅰ）.. …………………………3分 ‎（Ⅱ）设，.‎ 当时，，则函数为减函数.‎ 又因为，,‎ 所以有且只有一个，使成立.‎ 所以函数在区间内有且只有一个零点，即方程在区间内有且只有一个实数根. …………………………7分 ‎（Ⅲ）‎ 若函数在区间内有且只有一个极值点，由于，即在区间内有且只有一个零点，且在两侧异号.‎ 因为当时，函数为减函数，所以在上，，即成立，函数为增函数；‎ 在上， ，即成立，函数为减函数.‎ 则函数在处取得极大值.‎ 当时，虽然函数在区间内有且只有一个零点，但在 两侧同号，不满足在区间内有且只有一个极值点的要求.‎ 由于，显然.‎ 若函数在区间内有且只有一个零点，且在两侧异号，‎ 则只需满足：‎ ‎.即，解得. ……………………13分