- 2021-06-21 发布 |
- 37.5 KB |
- 5页

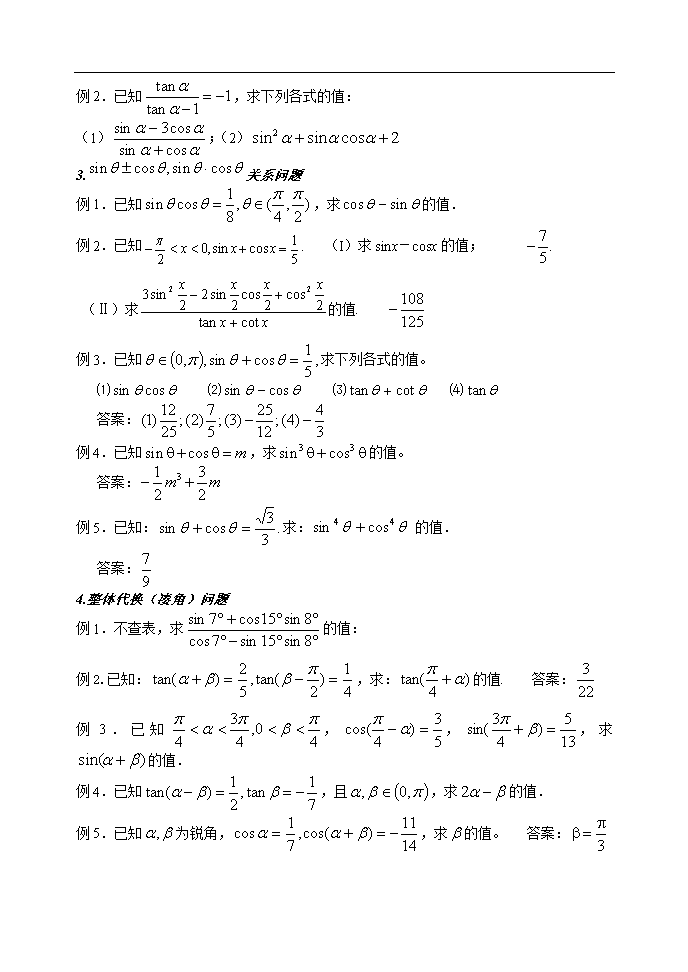

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高一三角函数知识点整理
第四章 三角函数 一.求值与化简 1.基本概念与公式(正用、逆用) 例1.已知锐角终边上一点的坐标为求角=( C ) (A) (B) (C)3 (D) 例2.. 答案:1 例3.化简:. 答案: 例4.化简: 答案: 例5.化简: 答案: 例6.化简: 答案: 例7.求值:.. 例8.化简 答案:—2 例9. ; 例10.若化简 答案: 例11.求的值 答案: 例12.求的值 答案: 例13.求的值 答案: 2.齐次式 例1.已知求下列各式的值。 (1) 答案: (2) 答案: (3) 答案: (4) 答案: 例2.已知,求下列各式的值: (1);(2) 3.关系问题 例1.已知,求的值. 例2.已知. (I)求sinx-cosx的值; (Ⅱ)求的值. 例3.已知求下列各式的值。 ⑴ ⑵ ⑶ ⑷ 答案: 例4.已知,求的值。 答案: 例5.已知:求:的值. 答案: 4.整体代换(凑角)问题 例1.不查表,求的值: 例2.已知:,求:的值. 答案: 例3.已知,,,求的值. 例4.已知,且,求的值. 例5.已知为锐角,,求的值。 答案: 例6.已知,,均为锐角,求的值。 答案: 例7.已知,,且,求的值.答案: 5.向量与三角综合 例1.已知向量, 求的值. 答案: 例2.已知向量, (1)求的值;(2)若的值。 答案:(1) ;(2) 6.三角形中的求值问题 例1.已知的三内角A、B、C称等差数列,且,求的值. 例2.已知是三角形三内角,向量,且.(Ⅰ)求角;(Ⅱ)若,求. 答案:(Ⅰ);(Ⅱ) 例3.已知、为的边,A、B分别是、的对角,且,求的值. 答案: 例4.在△ABC中,分别是A、B、C的对边,且, (1)求角B的大小; (2)若,求的值。 答案:(1);(2) 二.图像与性质 x y O -2 2 1.图像问题 例1.已知函数的一段图象如图所示;(1)求函数的解析式;(2)求这个函数的单调递增区间. 例2.作出的图像。 例3.根据正弦函数的图像求满足的范围。 答案: 例4.若函数的图像和直线围成一个封闭的平面图形,则这个封闭图形的面积为 例5.根据正切函数的图像,写出下列不等式的解集。 3 答案: 例6.求函数 的解析式. 答案: 例7.已知 图象如图 (1)求的解析式; (2)若与图象关于直线对称,求解析式. 例8.分析可由的图像如何变换得到。 例9.把函数的图象向右平移个单位,再把所得图象上各点的横坐标 缩短到原来的,得到怎样的解析式? 例10.要得到的图象,只要将的图象进行怎样的平移? 例11.简述将的图象变换为的图象的过程. 例12.把函数的图象向左平移个单位,所得的图象关于轴对称,则的最小值是( ) A. B. C. D. 例13.把函数的图形向左平移,所得图形对应的函数是 ( ) A.奇函数 B.偶函数 C.既是奇函数也是偶函数 D.既不是奇函数也不是偶函数 2.性质问题 例1.已知函数 (1)求函数的最小正周期; (2)写出函数的单调区间; (3)函数图象经过如何移动可得到函数的图象。 答案:(1);(2) 增区间;减区间;(3)将纵坐标变为原来,然后将所有点横坐标变为原来2倍,然后将所有点向左平移。 例2.已知函数,求函数的最小正周期和最大值. 例3.关于函数,下列命题正确的是________________ (1),可知是的整数倍;(2)表达式可改写为;(3)图象关于点对称;(4)图象关于对称.例4.设,则函数的最小值是( ) (A)3 (B)2 (C) (D) 例5.函数的图像的一条对称轴方程为( ) 例6.求函数的最小正周期. 例7.求函数的单调增区间. 例8.求函数的最大值和最小值. 例9.函数的图象的一条对称轴方程是 ( ) A. B. C. D. 例10.已知函数 (1)求函数的最小正周期;(2)求函数的最大值和最小值;(3)求函数的递增区间. 例11.如果函数的图像关于直线对称,那么 查看更多