- 2021-06-21 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年云南民族大学附属中学高二上学期期中考试数学(理)试题 解析版
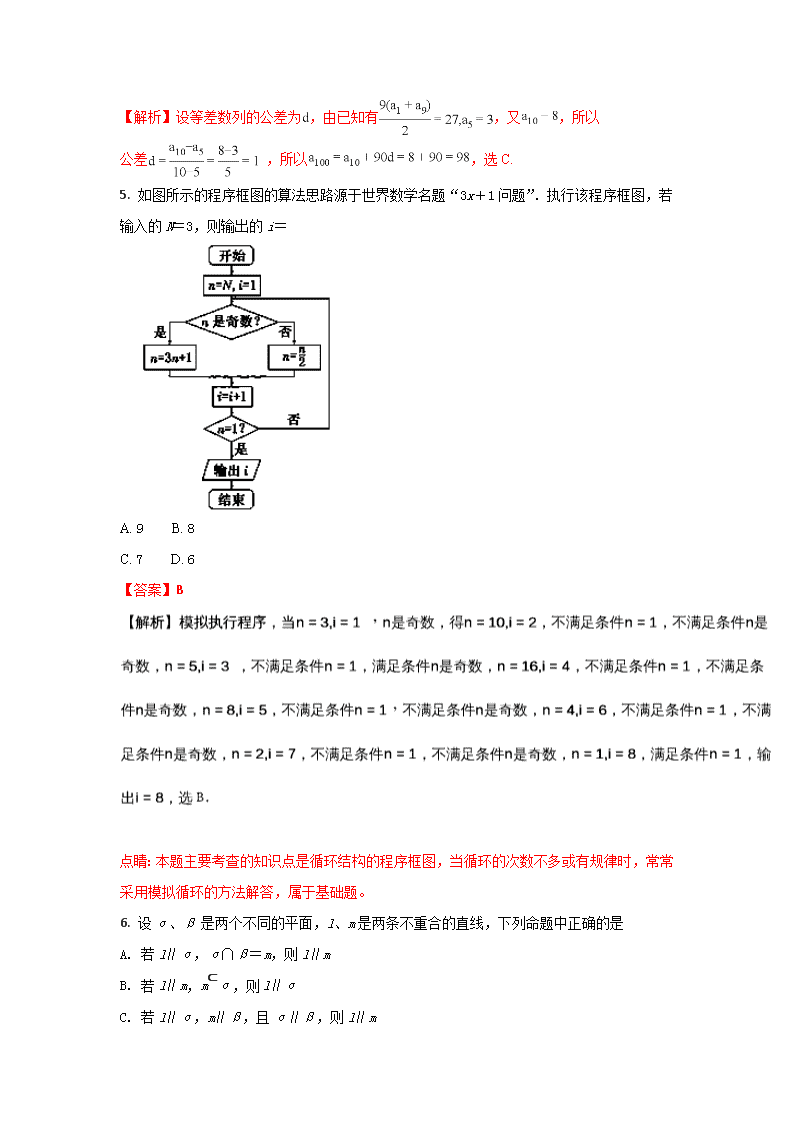
2017-2018 学年云南民族大学附属中学高二上学期期中考试 数学(理)试题 解析版 第Ⅰ卷 一.选择题(本大题共 12 小题,每小题 5 分,在每个小题给出的四个选项中, 只有一项是符合要求的) 1. 已知集合 A={x||x|<2},B={-1,0,1,2,3},则 A∩B= A. {0,1} B. {0,1,2} C. {-1,0,1} D. {-1,0,1,2} 【答案】C 【解析】集合 ,所以 ,选 C. 2. 若 f(x)是定义在 R 上的函数,则“f(0)=0”是“函数 f(x)为奇函数”的 A. 必要不充分条件 B. 充要条件 C. 充分不必要条件 D. 既不充分也不必要条件 【答案】A 【解析】由 函数 为奇函数,比如 ;因为 f(x)是定义在 R 上的函数, 所以函数 为奇函数 ,故“ ”是“函数 为奇函数”的必要非充分条件, 选 A. 点睛:本题主要考查奇函数的性质以及充分必要条件,属于易错题。本题要注意的是充分必 要条件的定义要弄懂。 3. 已知向量 a=(k,3),b=(1,4),c=(2,1),且(2a-3b)⊥c,则实数 k= A. - B. 0 C. 3 D. 【答案】C 【解析】 ,因为 , ,所以 ,选 C. 4. 已知等差数列{an}前 9 项的和为 27,a10=8,则 a100= A. 100 B. 99 C. 98 D. 97 【答案】C 【解析】设等差数列的公差为 ,由已知有 ,又 ,所以 公差 ,所以 ,选 C. 5. 如图所示的程序框图的算法思路源于世界数学名题“3x+1 问题”.执行该程序框图,若 输入的 N=3,则输出的 i= A. 9 B. 8 C. 7 D. 6 【答案】B 点睛:本题主要考查的知识点是循环结构的程序框图,当循环的次数不多或有规律时,常常 采用模拟循环的方法解答,属于基础题。 6. 设α、β是两个不同的平面,l、m 是两条不重合的直线,下列命题中正确的是 A. 若 l∥α,α∩β=m,则 l∥m B. 若 l∥m,m ⊂ α,则 l∥α C. 若 l∥α,m∥β,且α∥β,则 l∥m D. 若 l⊥α,m⊥β且α⊥β,则 l⊥m 【答案】D 【解析】对于选项 A,在用线面平行的性质定理时,必须有 ,才能得出 ,所以选项 A 错误;对于选项 B,缺少条件 ,不能得出 ;对于选项 C,不能得出 ,l、m 可 能异面,相交或平行,所以选项 C 错误;对于选项 D,直线 分别是平面 的法向量所在 直线,而 ,所以它们的法向量也互相垂直,D 正确,选 D. 7. 直线 l 过点(1,0),且倾斜角为直线 l0:x-2y-2=0 的倾斜角的 2 倍,则直线 l 的方程 为 A. 4x-3y-3=0 B. 3x-4y-3=0 C. 3x-4y-4=0 D. 4x-3y-4=0 【答案】D 【解析】设直线 的倾斜角为 ,则斜率 ,所以直线的倾斜角为 ,斜率 ,又经过点(1,0),所以直线方程为 ,即 ,选 D. 8. 函数 f(x)=sin 的图象的一条对称轴是 A. x= B. x= C. x=- D. x=- 【答案】C 【解析】试题分析:令 ,所以对称轴为 考点:三角函数性质 9. 正四棱锥的顶点都在同一球面上,若该棱锥的高为 4,底面边长为 2,则该球的表面积为 A. B. 16π C. 9π D. 【答案】A 在 Rt△ 中, ,由勾股定理 得 ,∴球的表面积 考点:球的体积和表面积 10. 等比数列{an}中,对任意正整数 n,a1+a2+a3+…+an=2n-1,则 a+a+a+…+a 等于 A. (4n-1) B. (2n-1) C. 4n-1 D. (2n-1)2 【答案】A 【解析】设等比数列 的公比为 ,由已知有 ,所以 ,所以数列 以首项 ,公比为 的等比数列,故有 ,选 A. 11. 已知函数 f(x)=2x+x,g(x)=log2x+x,h(x)=x3+x 的零点依次为 a,b,c,则 a, b,c 的大小关系为 A. a查看更多
- 当前文档收益归属上传用户