2014届高三理科数学一轮复习试题选编5：方程的解与函数的零点（教师版）

2014届高三理科数学一轮复习试题选编5：方程的解与函数的零点（教师版）

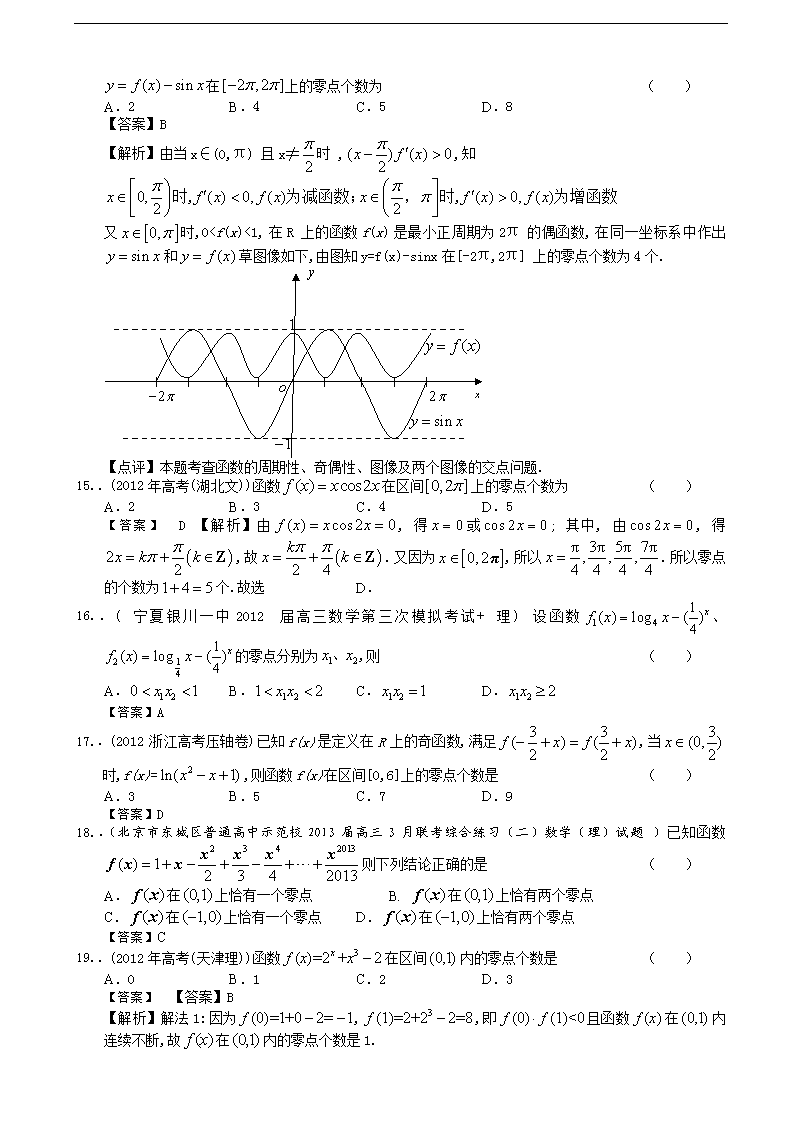
‎2014届高三理科数学一轮复习试题选编5：方程的解与函数的零点 一、选择题 ．（北京市海淀区2013届高三上学期期中练习数学（理）试题）“”是“函数在内存在零点”的 （　　）‎ A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件 ‎【答案】A ‎ ．（2013届北京市延庆县一模数学理）已知函数有且仅有两个不同的零点，，则 （　　）‎ A．当时，， B．当时，， ‎ C．当时，， D．当时，，‎ ‎【答案】B ．(2011年浙江省稽阳联谊学校高三联考数学理)已知函数在上恰有两个零点,则实数的取值范围为 （　　）‎ A． B． C． D．(2,4)‎ ‎【答案】D ‎ ．(2013重庆高考数学(理))若,则函数的两个零点分别位于区间 （　　）‎ A．和内 B．和内 C．和内 D．和内 ‎【答案】A．‎ ‎【解析】因为,,, ‎ 所以,,所以函数的两个零点分别在和内,,故选A． ‎ ‎【易错点】不能根据的大小进行判断函数值的符号,或错误利用零点存在性定理,造成错选B,C, D． ‎ ．(2013天津高考数学(理))函数的零点个数为 （　　）‎ A．1 B．‎2 ‎C．3 D．4‎ ‎【答案】 B．在同一坐标系中作出与,如图, ‎ ‎ ‎ 由图可得零点的个数为2. ‎ ．下列各种说法中正确的个数有 ‎ ‎①函数满足,则函数在区间内只有一个零点;‎ ‎②函数满足,则函数在区间内有零点;‎ ‎③函数满足,则函数在区间内没有零点;‎ ‎④函数在上连续且单调,并满足,则函数在区间内只有一个零点;‎ ‎⑤函数的零点是与. （　　）‎ A．0个 B．1个 C．2个 D．3个 ‎【答案】 B．‎ ．(2012年高考(湖北理))函数在区间上的零点个数为 （　　）‎ A．4 B．‎5 ‎C．6 D．7‎ ‎【答案】 考点分析:本题考察三角函数的周期性以及零点的概念. ‎ 解析:,则或,,又, ‎ 所以共有6个解.选 C． ‎ ．已知且方程恰有3个不同的实数根,则实数的取值范围是 ‎ ‎ ‎【答案】D ‎ ．（北京市昌平区2013届高三上学期期末考试数学理试题 ）已知函数，则函数的零点所在的区间是 （　　）‎ A．（0,1） B．（1,2） C．（2,3） D．（3,4）‎ ‎【答案】B 解：函数的导数为，所以。因为，，所以函数的零点所在的区间为.选 B．‎ ．（北京市朝阳区2013届高三上学期期中考试数学（理）试题）函数的图象与函数的图象的交点个数是 （　　）‎ A． B． C． D．‎ ‎【答案】C ‎ ．(2012年东城区高三一模数学理科)已知函数若方程有且只有两个不相等的实数根,则实数的取值范围是 （　　）‎ A． B． C． D．‎ ‎【答案】A ‎ ．(2012年高考(北京文))函数的零点个数为 （　　）‎ A．0 B．‎1 ‎C．2 D．3 ‎ ‎【答案】B ‎ ‎【解析】函数的零点,即令,根据此题可得,在平面直角坐标系中分别画出这两个函数的图像,可得交点只有一个,所以零点只有一个,故选答案 B． ‎ ．(黑龙江省哈三中高三第三次模拟理)已知函数 则下列关于函数的零点个数的判断正确的是 （　　）‎ A．当时,有3个零点;当时,有2个零点 ‎ B．当时,有4个零点;当时,有1个零点 ‎ C．无论为何值,均有2个零点 ‎ D．无论为何值,均有4个零点 ‎【答案】B ‎ ．(2012年高考(湖南文))设定义在上的函数是最小正周期为的偶函数,是的导函数,当时,;当且时 ,,则函数在 上的零点个数为 （　　）‎ A．2 B．‎4 ‎C．5 D．8 ‎ ‎【答案】B ‎ ‎【解析】由当x∈(0,π) 且x≠时 ,,知 ‎ ‎ ‎ 又时,0

查看更多