2021届课标版高考文科数学大一轮复习课件：§4-4 解三角形（讲解部分）

2021届课标版高考文科数学大一轮复习课件：§4-4 解三角形（讲解部分）

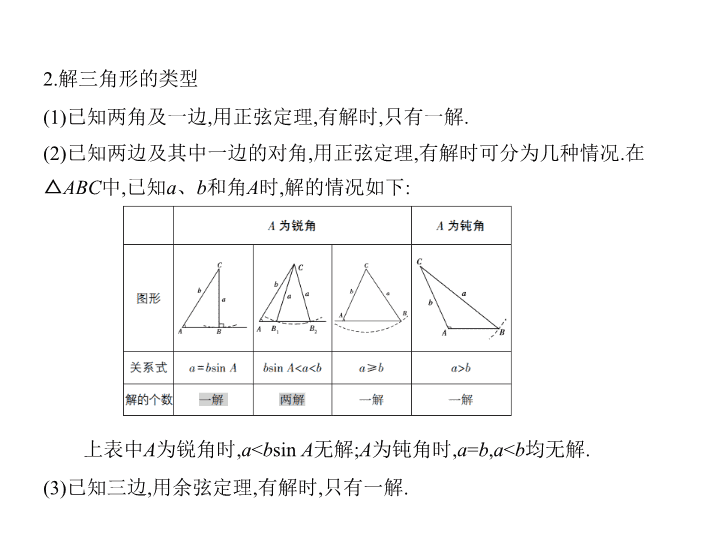
考点一　正弦定理与余弦定理 考点清单 考向基础 1.正、余弦定理 2.解三角形的类型 (1)已知两角及一边,用正弦定理,有解时,只有一解. (2)已知两边及其中一边的对角,用正弦定理,有解时可分为几种情况.在 △ ABC 中,已知 a 、 b 和角 A 时,解的情况如下: 　　上表中 A 为锐角时, a < b sin A 无解; A 为钝角时, a = b , a < b 均无解. (3)已知三边,用余弦定理,有解时,只有一解. (4)已知两边及夹角,用余弦定理,必有一解. 考向突破 考向一　利用正、余弦定理解三角形 例1    (2019安徽安庆二模,7)若△ ABC 的内角 A , B , C 所对的边分别为 a , b , c ,已 知 b sin 2 A = a sin B ,且 c =2 b ,则   等于   (　　) A.   　    B.   　    C.   　    D.   解析　由 b sin 2 A = a sin B 及正弦定理得2sin B sin A cos A =sin A sin B ,又 A , B ∈ (0,π),所以sin A ≠ 0,sin B ≠ 0,所以cos A =   .又 c =2 b ,所以由余弦定理得 a 2 = b 2 + c 2 -2 bc cos A = b 2 +4 b 2 -4 b 2 ×   =3 b 2 ,得   =   .故选D. 答案    D 例2    (2017课标全国Ⅱ,16,5分)△ ABC 的内角 A , B , C 的对边分别为 a , b , c ,若 2 b cos B = a cos C + c cos A ,则 B = 　　　     . 解析　解法一:由正弦定理得2sin B cos B =sin A cos C +sin C ·cos A ,即sin 2 B = sin( A + C ),即sin 2 B =sin(180 ° - B ),可得 B =60 ° . 解法二:由余弦定理得2 b ·   = a ·   + c ·   ,即 b ·   = b ,所以 a 2 + c 2 - b 2 = ac ,所以cos B =   ,又0 ° < B <180 ° ,所以 B =60 ° . 答案　60 °   思路分析    利用正弦定理或余弦定理将边角统一后求解. 考向二　利用正、余弦定理判断三角形的形状 例3　在△ ABC 中,角 A , B , C 所对的边分别是 a , b , c ,若直线 bx + y cos A +cos B =0 与 ax + y cos B +cos A =0平行,则△ ABC 一定是   (　　) A.锐角三角形　    B.等腰三角形 C.直角三角形　    D.等腰或者直角三角形 解析　解法一:由两直线平行可得 b cos B - a cos A =0,由正弦定理可知 sin B cos B -sin A cos A =0,即   sin 2 A =   sin 2 B ,又 A , B ∈(0,π),且 A + B ∈(0,π),所以 2 A =2 B 或2 A +2 B =π,即 A = B 或 A + B =   .若 A = B ,则 a = b ,cos A =cos B ,此时两直线 重合,不符合题意,舍去,故 A + B =   ,则△ ABC 是直角三角形,故选C. 解法二:由两直线平行可得 b cos B - a cos A =0,由余弦定理,得 a ·   = b ·   ,所以 a 2 ( b 2 + c 2 - a 2 )= b 2 ( a 2 + c 2 - b 2 ),所以 c 2 ( a 2 - b 2 )=( a 2 + b 2 )( a 2 - b 2 ),所以( a 2 - b 2 )( a 2 + b 2 - c 2 )=0,所以 a = b 或 a 2 + b 2 = c 2 .若 a = b ,则两直线重合,不符合题意,故 a 2 + b 2 = c 2 ,则△ ABC 是直角三角形,故选C. 答案    C 考向基础 1.三角形的面积 设△ ABC 的三边 a , b , c 所对的三个内角为 A , B , C ,其面积为 S ,外接圆半径为 R . (1) S =   ah ( h 为 BC 边上的高); (2) S =   ab sin C =   ac sin B =   bc sin A ; (3) S =2 R 2 sin A sin B sin C ; (4) S =   ; (5) S =     . 考点二　解三角形及其应用 2.实际问题中的常用角 (1)仰角和俯角 与目标视线在同一铅垂平面内的水平线和目标视线的夹角,目标视线在水 平线上方的角叫 仰角 ,目标视线在水平线下方的角叫 俯角 (如图a).   (2)方位角 方位角是指从某点的 正北 方向顺时针转到目标方向线的水平角,如 B 点的 方位角为 α (如图b). (3)坡角:坡面与水平面所成的锐二面角. 【知识拓展】 在△ ABC 中,角 A , B , C 所对的边分别是 a , b , c ,常见的结论如下: (1) A + B + C =π ; (2)在△ ABC 中,大角对大边,大边对大角,如: a > b ⇔ A > B ⇔ sin A >sin B ; (3)任意两边之和大于第三边,任意两边之差小于第三边; (4)在锐角三角形 ABC 中, sin A >cos B ⇔ A + B >   ; (5)在斜△ ABC 中, tan A +tan B +tan C =tan A ·tan B ·tan C ; (6)有关三角形内角的常用三角恒等式:sin( A + B )=sin C ,cos( A + B )=-cos C , tan( A + B )=-tan C   ,sin   =cos   ,cos   =sin   . 考向一　求三角形的面积 考向突破 例4    (2019福建厦门一模,8)在△ ABC 中,cos B =   , b =2,sin C =2sin A ,则 △ ABC 的面积等于   (　　) A.   　    B.   　    C.   　    D.   解析　在△ ABC 中,cos B =   , b =2,sin C =2sin A ,所以由正弦定理得 c =2 a ;由余 弦定理得 b 2 = a 2 + c 2 -2 ac ·cos B = a 2 +4 a 2 -2 a ·2 a ·   =4 a 2 =4,解得 a =1,可得 c =2,所以 △ ABC 的面积 S =   ac sin B =   × 1 × 2 ×   =   .故选D. 答案    D 考向二　解三角形在实际问题中的应用 例5    (2020届河南新乡调研,15)如图,为测量某山峰的高度(即 OP 的长),选 择与 O 在同一水平面上的 A , B 为观测点.在 A 点测得山顶 P 的仰角为45 ° ,在 B 处测得山顶 P 的仰角为60 ° .若 AB =30米,∠ AOB =30 ° ,则山峰的高为 　　　     米.   解析　设 OP = h ,由题意可知 OA = h , OB =   h .在△ AOB 中,由余弦定理可得30 2 = h 2 +   -2 h ×   h cos 30 ° ,解得 h =30   (负根舍去),故山峰的高度为 30   米. 答案　30   方法1 　利用正、余弦定理判断三角形形状的方法 1.通过正弦定理、余弦定理化边为角,利用三角恒等变换得出三角形内角 之间的关系并进行判断. 2.利用正弦定理、余弦定理化角为边,通过代数恒等变换,求出三条边之间 的关系并进行判断. 方法技巧 例1　设△ ABC 的内角 A , B , C 所对的边分别为 a , b , c . (1)若 b cos C + c cos B = a sin A ,判断△ ABC 的形状; (2)若sin A ∶sin B ∶sin C =5∶11∶13,判断△ ABC 的形状; (3)若 a 2 + b 2 - c 2 = ab ,且2cos A sin B =sin C ,试判断△ ABC 的形状. 解析　(1)由正弦定理得sin B cos C +sin C cos B =sin 2 A , ∴sin( B + C )=sin 2 A ,即sin(π- A )=sin 2 A ,sin A =sin 2 A . ∵ A ∈(0,π),∴sin A >0,∴sin A =1,∴ A =   , ∴△ ABC 是直角三角形. (2)在△ ABC 中,sin A ∶sin B ∶sin C =5∶11∶13, ∴ a ∶ b ∶ c =5∶11∶13, 可设 a =5 k , b =11 k , c =13 k ( k >0),由余弦定理可得 cos C =   =   =-   <0, 又∵ C ∈(0,π),∴ C ∈   ,∴△ ABC 为钝角三角形. (3)解法一:由正弦定理知   =   , ∵2cos A sin B =sin C ,∴cos A =   =   , 又由余弦定理得cos A =   , ∴   =   ,即 c 2 = b 2 + c 2 - a 2 , ∴ a 2 = b 2 ,∴ a = b . 又∵ a 2 + b 2 - c 2 = ab , ∴2 b 2 - c 2 = b 2 ,∴ b 2 = c 2 ,∴ b = c ,∴ a = b = c . ∴△ ABC 为等边三角形. 解法二:∵ A + B + C =180 ° ,∴sin C =sin( A + B ), 又∵2cos A sin B =sin C , ∴2cos A sin B =sin A cos B +cos A sin B , ∴sin( A - B )=0, 注意到 A 与 B 均为△ ABC 的内角,∴ A = B , 又 a 2 + b 2 - c 2 = ab ,∴cos C =   =   =   , ∵0 ° < C <180 ° ,∴ C =60 ° ,∴△ ABC 为等边三角形. 方法2 　求解三角形实际问题的方法 1.解三角形应用题的两种方法 (1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可 用正弦定理或余弦定理求解; (2)实际问题抽象概括后,已知量与未知量涉及两个或两个以上三角形,这 时需作出这些三角形,先解条件已知的三角形,然后逐步求出其他三角形的 解,有时需设出未知量,从几个三角形中列出方程,解方程得出所求的解. 2.解三角形应用题应注意的问题 (1)要注意仰角、俯角、方位角以及方向角等名词,并能准确地找出这些角; (2)要注意将平面几何中的性质、定理与正、余弦定理结合起来使用,这样 可以优化解题过程; (3)注意题目中的隐含条件以及解的实际意义. 例2　如图,在海岛 A 上有一座海拔1千米的山,山顶设有一个观察站 P ,上午 11时,测得一轮船在海岛北偏东30 ° ,俯角为30 ° 的 B 处,到11时10分又测得该 船在海岛北偏西60 ° ,俯角为60 ° 的 C 处. (1)求船的航行速度; (2)又经过一段时间后,船到达海岛的正西方向的 D 处,问此时船距海岛 A 有 多远?     解析　(1)在Rt△ PAB 中,∠ APB =60 ° , PA =1,∴ AB =   . 在Rt△ PAC 中,∠ APC =30 ° ,∴ AC =   . 在△ ACB 中,∠ CAB =30 ° +60 ° =90 ° , ∴ BC =   =   =   . 则船的航行速度为   ÷   =2   (千米/时). (2)在△ ACD 中,∠ DAC =90 ° -60 ° =30 ° , sin∠ DCA =sin(180 ° -∠ ACB )=sin∠ ACB =   =   =     ,sin∠ CDA =sin (∠ ACB -30 ° )=sin∠ ACB cos 30 ° -cos∠ ACB ·sin 30 ° =     ×   -   ×   =   . 在△ ACD 中,由正弦定理得   =   . ∴ AD =   =   =   . 故此时船距海岛 A 有   千米.