数学理卷·2017届湖北省武汉市武昌区高三年级元月调研考试（2017

数学理卷·2017届湖北省武汉市武昌区高三年级元月调研考试（2017

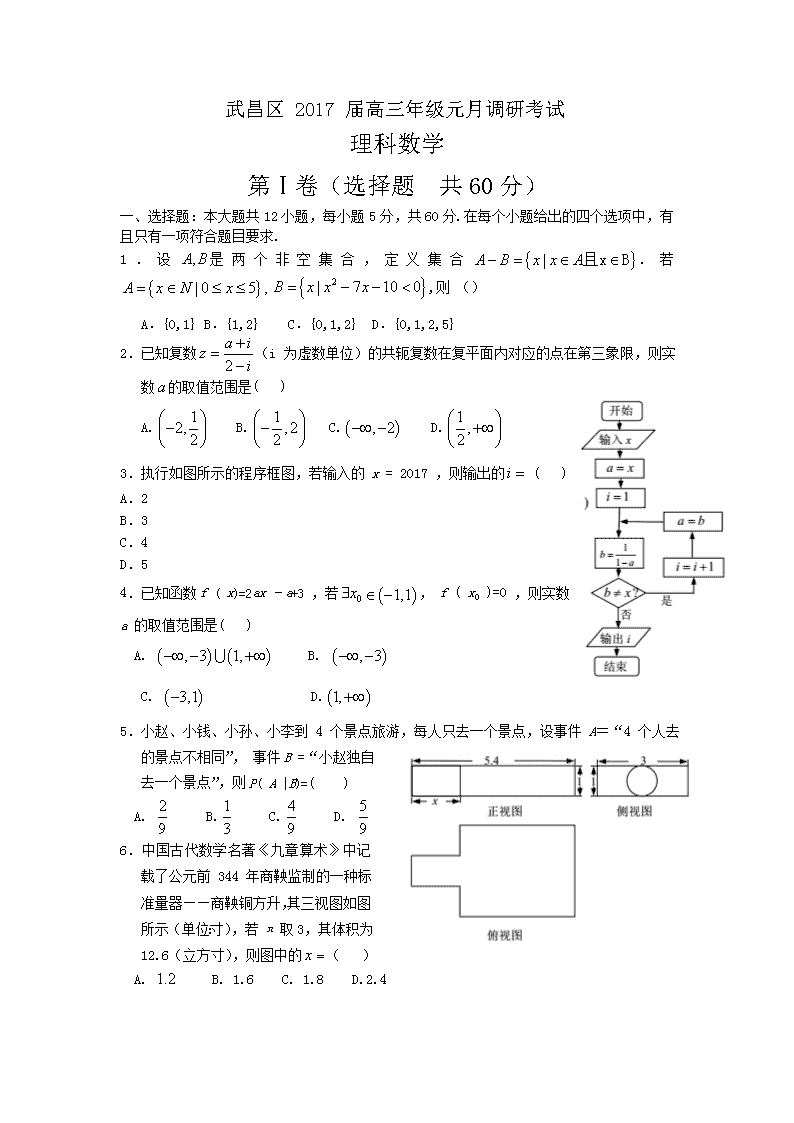
武昌区 2017 届高三年级元月调研考试 理科数学 第Ⅰ卷（选择题 共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.‎ ‎1．设是两个非空集合，定义集合．若,则 （）‎ ‎ ‎ A．{0,1} B．{1,2} C．{0,1,2} D．{0,1,2,5}‎ ‎2．已知复数（i 为虚数单位）的共轭复数在复平面内对应的点在第三象限，则实 ‎ ‎ 数的取值范围是( )‎ A. B. C. D.‎ ‎3．执行如图所示的程序框图，若输入的 x = 2017 ，则输出的 ( )‎ A．2‎ B．3‎ ‎ ‎ C．4‎ ‎ ‎ D．5‎ ‎4．已知函数f ( x)=2ax –a+3 ，若， f ( x0 )=0 ，则实数 a 的取值范围是( )‎ ‎ A. B. ‎ ‎ C. D.‎ ‎5．小赵、小钱、小孙、小李到 4 个景点旅游，每人只去一个景点，设事件 A＝“4 个人去的景点不相同”， 事件B =“小赵独自去一个景点”，则P( A |B)=( )‎ ‎ A. B. C. D. ‎ ‎6．中国古代数学名著《九章算术》中记载了公元前 344 年商鞅监制的一种标准量器——商鞅铜方升，其三视图如图所示（单位：寸），若π取3，其体积为 12.6（立方寸），则图中的（ ）‎ ‎ A. B. 1.6 C. 1.8 D.2.4‎ ‎ 7.若的展开式中所有项系数的绝对值之和为1024，则该展开式中的常数项是（ ）‎ A. -270 B. 270 C. -90 D.90‎ ‎8．一名法官在审理一起珍宝盗窃案时，四名嫌疑人甲、乙、丙、丁的供词如下，甲说：“罪犯在乙、丙、丁三人之中”；乙说：“我没有作案，是丙偷的”；丙说：“甲、乙两人中有一人是小偷”；丁说：“乙说的是事实”．经过调查核实，四人中有两人说的是真话，另外两人说的是假话，且这四人中只有一人是罪犯，由此可判断罪犯是( )‎ ‎ A. 甲 B. 乙 C.丙 D.丁 ‎9．已知函数 f ( x) 的部分图象如图所示，则 f ( x) 的解析式可以是（ ）‎ ‎ A. B. ‎ ‎ C. D. ‎ ‎10.设 x，y 满足约束条件且的最小值为7，则( )‎ ‎ A. -5 B. 3 C. -5或3 D.5或-3‎ ‎11. 已知双曲线的两条渐近线分别为，经过右焦点F垂直于的直线分别交l1 ，l2 于 A，B 两点．若|OA|，|AB|，|OB|成等差数列，且与反向，则该双曲线的离心率为( )‎ ‎ A. B. C. D.‎ ‎12. 在锐角三角形ABC 中，角 A，B，C 的对边分别为 a，b，c．若，则的最小值是( )‎ ‎ ‎ A. 4 B. C. 8 D.‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13. 13．已知抛物线 Γ：y2 = 8x 的焦点为 F，准线与 x 轴的交点为K，点 P 在 Γ 上且,则的面积为 .‎ ‎14.函数的最大值为 .‎ ‎15. 已知平面向量的夹角为 120°，且．若平面向量 满足，则 .‎ ‎16.若四面体 ABCD 的三组对棱分别相等，即 AB=CD ，AC=BD ，AD=BC ．‎ 给出下列结论：‎ ‎ ‎ ‎①四面体 ABCD 每组对棱相互垂直；‎ ‎ ‎ ‎②四面体 ABCD 每个面的面积相等；‎ ‎③从四面体 ABCD 每个顶点出发的三条棱两两夹角之和大于而小于；‎ ‎④连接四面体 ABCD 每组对棱中点的线段相互垂直平分；‎ ‎⑤从四面体 ABCD 每个顶点出发的三条棱的长可作为一个三角形的三边长．‎ 其中正确结论的序号是 .（写出所有正确结论的序号） ‎ 三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程.‎ ‎17.（本题满分12分）‎ 设等差数列{an }的前n项和为Sn，已知a1=9 ，a2为整数，且 ‎（1）求{an }的通项公式；‎ ‎ （2）设数列的前项和为，求证：‎ ‎18.（本题满分12分）‎ 如图，四棱锥中，AB∥CD，BC⊥CD，侧面 SAB 为等边三角形，AB=BC=2，‎ ‎ ‎ CD=SD=1 ．‎ ‎ ‎ ‎（Ⅰ）证明：SD⊥平面 SAB；‎ ‎（Ⅱ）求 AB 与平面 SBC 所成角的正弦值．‎ ‎18.（本题满分12分）‎ 我国是世界上严重缺水的国家，城市缺水问题较为突出．某市政府为了鼓励居民节约用水，计划在本市试行居民生活用水定额管理，即确定一个合理的居民月用水量标准 x ‎（吨），用水量不超过 x 的部分按平价收费，超出 x 的部分按议价收费．为了了解全市居民用水量的 分布情况，通过抽样，获得了 100 位居民某年的月均用水量（单位：吨），将数据按照[0,0.5) ，‎ ‎[0.5,1) ，…，[4,4.5]分成9组，制成了如图所示的频率分布直方图．‎ ‎（Ⅰ）求直方图中 a 的值；‎ ‎（Ⅱ）若该市政府希望使 85﹪的居民每月的用水量不超过标准 x（吨），估计 x 的值，并说明理由；‎ ‎（Ⅲ）已知平价收费标准为 4 元/吨，议价收费标准为 8元/吨．当 x=3时，估计该市居民的月平均水费．（同一组中的数据用该组区间的中点值代替）‎ ‎20.（本题满分12分）‎ ‎ 已知椭圆的中心在坐标原点，是它的两个顶点，直线与AB相交于点D，与椭圆相交于E,F两点.‎ ‎ （1）若，求的值；‎ ‎ （2）求四边形AEBF面积的最大值.‎ ‎21.（本题满分12分）‎ ‎ 已知函数 ‎ （1）讨论的单调性；‎ ‎ （2）设，证明：当时，；‎ ‎ （3）设是的两个零点，证明：‎ 请考生在第22、23两题中任选一题作答，如果两题都做，则按照所做的第一题给分；作答时，请用2B铅笔将答题卡上相应的题号涂黑。‎ ‎22.（本题满分10分）选修4-4：坐标系与参数方程 ‎ 在直角坐标系中，曲线的C的参数方程为（为参数，‎ ‎）.以坐标原点为极点，轴的正半轴为极轴建立极坐标系，已知直线的极坐标方程为 ‎（1）设P是曲线C上的一个动点，当时，求点P到直线的距离的最小值；‎ ‎（2）若曲线C上的所有点均在直线的右下方，求的取值范围.‎ ‎ ‎ ‎23.（本题满分10分）选修4-5：不等式选讲 ‎ 设函数，记的解集为M.‎ ‎（1）求M,‎ ‎（2）当时，证明：.‎ 武昌区 2017 届高三年级元月调研考试 理科数学参考答案 一、 选择题：‎ ‎1-5，DABAA, 6-10，BCBDB, 11、12,CC 二、填空题：‎ ‎ 13.8， 14.4 15. 16.②④⑤‎ 三、解答题：‎ ‎17. ‎ ‎18. ‎ ‎ ‎ ‎ ‎ ‎19. ‎ ‎ ‎ ‎20. ‎ ‎ ‎ ‎21. ‎ ‎22. ‎ ‎23. ‎