天津市和平区2020届高三上学期期末统考 数学试题（PDF版含答案）

天津市和平区2020届高三上学期期末统考 数学试题（PDF版含答案）

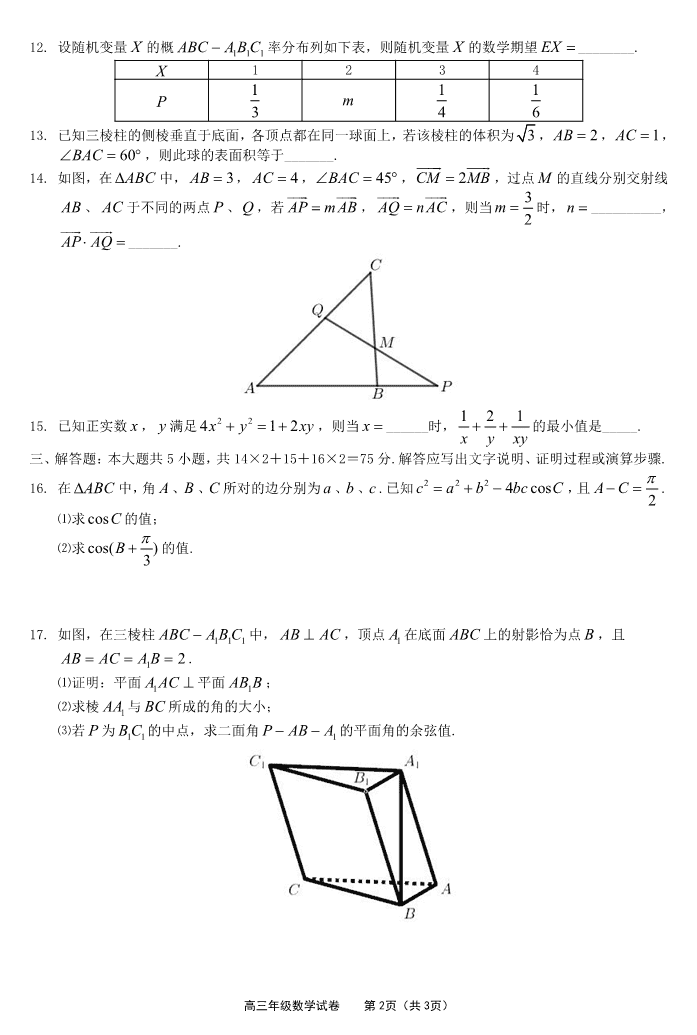
高三年级数学试卷 第 1页（共 3页） 天津市和平区 2019～2020 学年度高三年级上学期期末考试 一、选择题：本大题共 9 小题，每小题 5 分，共 45 分.在每小题给出的四个选项中，只有一项是符合题目 要求的. 1. 设全集为 R ，集合 { | 1 3}A x Z x     ，集合 {B  1，2}，则集合 ( )RA B  ð （ ） A.{ 1 ， 0} B. ( 1 ，1) (2 ， 3] C. (0 ，1) (1 ， 2) (2 ， 3] D.{0 ，3} 2. 设 x R ，则“ 2 1x   ”是“ 2 4 3 0x x   ”的（ ） A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件 3. 奇函数 ( )f x 在区间[3 ，6] 上是增函数，在区间[3 ， 6]上的最大值为 8，最小值为  1，则 (6)f ( 3)f  的值为（ ） A.  10 B.15 C.10 D.9 4. 已知圆的半径为 2，圆心在 x 轴的正半轴上，且与直线3 4 4 0x y   相切，则圆的方程是（ ） A. 2 2 4 0x y x   B. 2 2 4 0x y x   C. 2 2 2 3 0x y x    D. 2 2 2 3 0x y x    5. 设 0.22a  ， 3log 0.9b  ， 0.11 log 4c   ，则 a ， b ， c 的大小关系是（ ） A. a c b  B.b c a  C. c a b  D. c b a  6. 将函数 sin( )cos( )2 2y x x    的图象沿 x 轴向左平移 8  个单位后，得到一个偶函数的图象，则 的取值不可能是（ ） A. 3 4  B. 4  C. 4  D. 5 4  7. 抛物线 2 8y x 的焦点 F 是双曲线 2 2 2 2 1( 0x y aa b    ， 0)b  的一个焦点， (A m ， )( 0)n n  为抛 物线上一点，直线 AF 与双曲线有且只有一个交点，若 8AF  ，则该双曲线的离心率为（ ） A. 2 B. 3 C.2 D. 5 8. 某中学组织高三学生进行一项能力测试，测试内容包括 A 、 B 、C 三个类型问题，这三个类型所含 题目的个数分别占总数的 1 2 ， 1 3 ， 1 6 .现有 3 名同学独立地从中任选一个题目作答，则他们选择的题 目所属类型互不相同的概率为（ ） A. 1 36 B. 1 12 C. 1 6 D. 1 3 9. 已知函数 2 2 log ( 1) 1 1 0 ( ) 2 0 x x f x x x xx           .若方程 ( ) 1f x kx  有两个实根，则实数 k 的取值 范围是（ ） A. 1(2 ， 2) B.(1， 2 ]ln2 C. (1， 2] D. 1(2 ， 2 )ln2 二、填空题：本大题共 6 小题，每小题 5 分，共 30 分. 10. 设i 是虚数单位，复数 2 a i i  的模为 1，则正数 a 的值为_______. 11. 已知 0a  ， 6 2( )ax x  的二项展开式中，常数项等于 60，则 6 2( )ax x  的展开式中各项系数和为____ （用数字作答）. 高三年级数学试卷 第 2页（共 3页） 12. 设随机变量 X 的概 1 1 1ABC A B C 率分布列如下表，则随机变量 X 的数学期望 EX  ________. X 1 2 3 4 P 1 3 m 1 4 1 6 13. 已知三棱柱的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为 3 ， 2AB  ， 1AC  ， 60BAC   ，则此球的表面积等于_______. 14. 如图，在 ABC 中， 3AB  ， 4AC  ， 45BAC   ， 2CM MB  ，过点 M 的直线分别交射线 AB 、 AC 于不同的两点 P 、Q ，若 AP mAB  ， AQ nAC  ，则当 3 2m  时， n  __________， AP AQ   _______. 15. 已知正实数 x ， y 满足 2 24 1 2x y xy   ，则当 x  ______时， 1 2 1 x y xy   的最小值是_____. 三、解答题：本大题共 5 小题，共 14×2＋15＋16×2＝75 分.解答应写出文字说明、证明过程或演算步骤. 16. 在 ABC 中，角 A 、B 、C 所对的边分别为 a 、b 、c .已知 2 2 2 4 cosc a b bc C   ，且 2A C   . ⑴求 cosC 的值； ⑵求 cos( )3B  的值. 17. 如图，在三棱柱 1 1 1ABC A B C 中， AB AC ，顶点 1A 在底面 ABC 上的射影恰为点 B ，且 1 2AB AC A B   . ⑴证明：平面 1A AC  平面 1AB B ； ⑵求棱 1AA 与 BC 所成的角的大小； ⑶若 P 为 1 1B C 的中点，求二面角 1P AB A  的平面角的余弦值. 高三年级数学试卷 第 3页（共 3页） 18. 已知椭圆 C ： 2 2 2 2 1( 0)x y a ba b     的左、右焦点分别为 1F 、 2F ，离心率为 1 2 ，点 P 是椭圆C 上 的一个动点，且 1 2PF F 面积的最大值为 3 . ⑴求椭圆C 的方程； ⑵过点 (0M ，1) 作直线 1l 交椭圆C 于 A 、B 两点，过点 M 作直线 1l 的垂线 2l 交圆O ： 2 2 2 4 ax y  于另一点 N .若 ABN 的面积为 3，求直线 1l 的斜率. 19. 已知等比数列{ }na 的公比 1q  ，且 3 4 5 28a a a   ， 4 2a  是 3a 、 5a 的等差中项. ⑴求数列{ }na 的通项公式； ⑵试比较 1 1 2( 1)( 1) n k k k k a a a    与 1 2 的大小，并说明理由； ⑶若数列{ }nb 满足 * 2 1log ( )n nb a n N  ，在每两个 kb 与 1kb  之间都插入 1 *2 ( )k k N  个 2，使得数 列{ }nb 变成了一个新的数列{ }pc ，试问：是否存在正整数 m ，使得数列{ }pc 的前 m 项和 2019mS  ？ 如果存在，求出 m 的值；如果不存在，说明理由. 20. 设函数 ( ) xf x ae ， ( ) lng x x b  ，其中 a ， b R ， e 是自然对数的底数. ⑴设 ( ) ( )F x xf x ，当 1a e 时，求 ( )F x 的最小值； ⑵证明：当 1a e ， 1b  时，总存在两条直线与曲线 ( )y f x 与 ( )y g x 都相切； ⑶当 2 2a e  时，证明： ( ) [ ( ) ]f x x g x b  . 高三年级数学试卷 第 1页（共 6页） 参考答案 高三年级数学试卷 第 2页（共 6页） 高三年级数学试卷 第 3页（共 6页） 高三年级数学试卷 第 4页（共 6页） 高三年级数学试卷 第 5页（共 6页） 高三年级数学试卷 第 6页（共 6页）