北京市2020届高三数学文一轮复习典型题专项训练：立体几何

北京市2020届高三数学文一轮复习典型题专项训练：立体几何

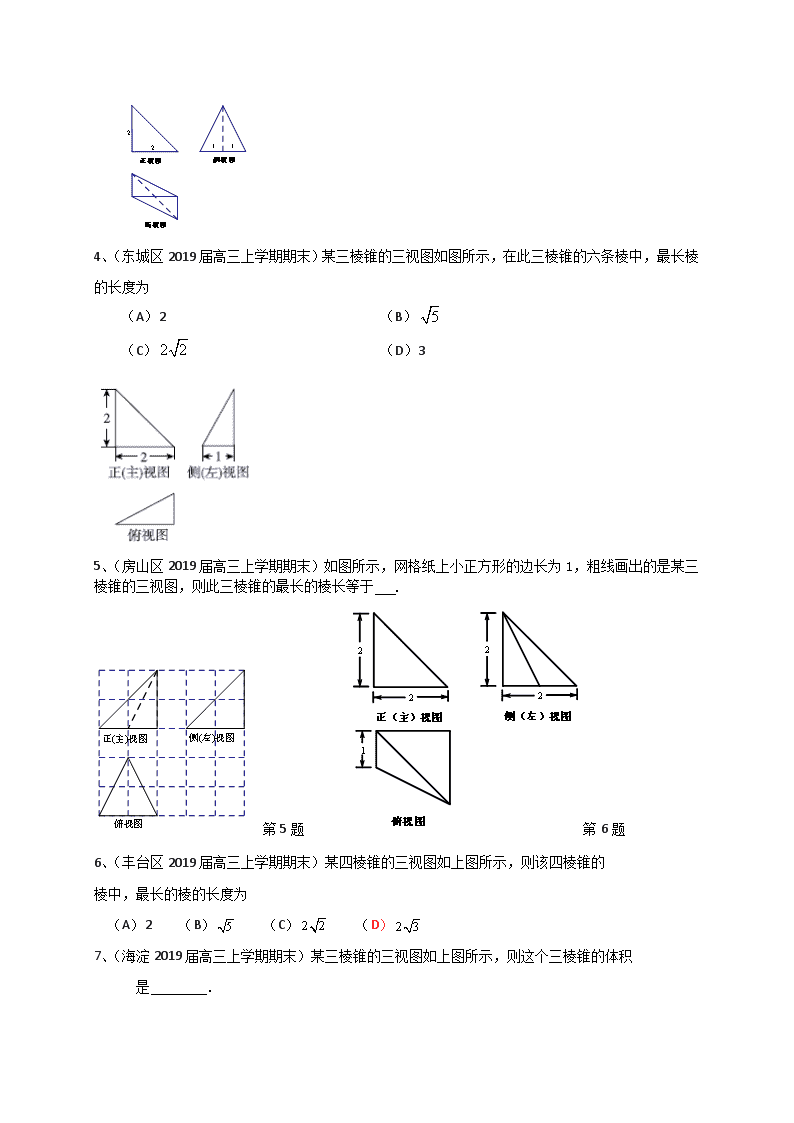
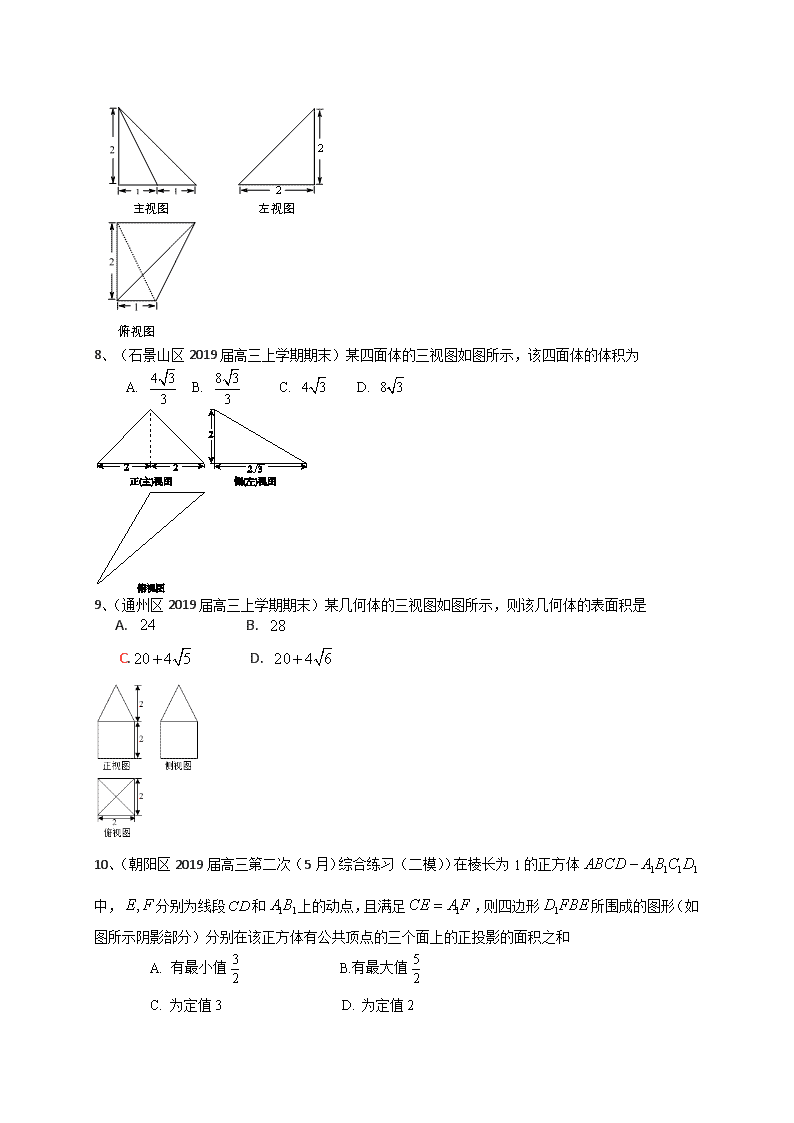
北京市2020届高三数学文一轮复习典型题专项训练 立体几何 一、选择、填空题 ‎1、（昌平区2019届高三上学期期末）《九章算术》是我国古代数学著作，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问：积及米几何？”其意思为：在屋内墙角处堆放米（米堆所形成的几何体的三视图如图所示），米堆底部的弧长为尺，米堆的高为尺，问米堆的体积及堆放的米各为多少？‎ 已知一斛米的体积约为立方尺，由此估算出堆放的米约有 A．斛 B．斛 C．斛 D．斛 ‎2、（朝阳区2019届高三上学期期末）如图，在边长为的正方形网格中，粗实线表示一个三棱锥的三视图，则该三棱锥的表面积为 ． ‎ ‎3、（大兴区2019届高三上学期期末）某三棱锥的三视图如图所示，则该三棱锥的体积为 ‎（A） （B） （C） （D）‎ ‎4、（东城区2019届高三上学期期末）某三棱锥的三视图如图所示，在此三棱锥的六条棱中，最长棱的长度为 ‎（A）2 （B）‎ ‎（C） （D）3‎ ‎5、（房山区2019届高三上学期期末）如图所示，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则此三棱锥的最长的棱长等于 .‎ ‎　第5题　　　第6题 ‎6、（丰台区2019届高三上学期期末）某四棱锥的三视图如上图所示，则该四棱锥的 棱中，最长的棱的长度为 ‎（A）2　　（B）　　（C）　　（D）‎ ‎7、（海淀2019届高三上学期期末）某三棱锥的三视图如上图所示，则这个三棱锥的体积是 ． ‎ ‎8、（石景山区2019届高三上学期期末）某四面体的三视图如图所示，该四面体的体积为 ‎ ‎ A. 　B. 　　C. 　　D. ‎ ‎9、（通州区2019届高三上学期期末）某几何体的三视图如图所示，则该几何体的表面积是 A. B. ‎ C. D. ‎ ‎10、（朝阳区2019届高三第二次（5月）综合练习（二模））在棱长为1的正方体中，分别为线段和上的动点，且满足，则四边形所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和 A. 有最小值 B.有最大值 ‎ ‎ C. 为定值 D. 为定值 ‎11、（东城区2019届高三5月综合练习（二模））鲁班锁起源于中国古代建筑中首创的榫卯结构，相传由春秋时代鲁国工匠鲁班所作. 右图是经典的六柱鲁班锁及六个构件的图片，下图是其中一个构件的三视图，则此构件的体积为 ‎ ‎（A） （B） （C） （D）‎ ‎12、（丰台区2019届高三5月综合练习（二模））某三棱锥的三视图如图所示，则该三棱锥的体积为 ‎（A）　　（B）　　（C）　　（D）‎ ‎13、（海淀区2019届高三5月期末考试（二模））某三棱锥的三视图如右图所示，则该三棱锥的所有棱长构成的集合为 ‎ (A) 　　(B) ‎ ‎ (C) 　 (D) ‎ ‎14、（丰台区2019届高三一模）已知两条直线与两个平面，下列命题正确的是 ‎（A）若， 则　　（B）若， 则 ‎（C）若， 则　　（D）若，则 ‎15、（怀柔区2019届高三一模）某三棱锥的三视图如图所示，则该三棱锥最长的棱长为 A． B． C． D．‎ ‎16、（门头沟区2019届高三一模）一个体积为的正三棱柱的三视图如图所示，则这个三棱柱的左视图的面积为 A. B．8 C． D．12‎ ‎ ‎ ‎17、（顺义区2019届高三第二次统练（一模））某几何体的三视图如下图所示,则该几何体的表面积是 A．12 B. 2 C. D. ‎ ‎18、（西城区2019届高三一模）某四棱锥的三视图如图所示，那么该四棱锥的体积为____． ‎ 参考答案：‎ ‎1、A 2、 3、A 4、D 5、3‎ ‎6、D 7、 8、A 9、C 10、D ‎11、C 12、B 13、C 14、B ‎15、C　　　16、A　　17、D　　17、　‎ 二、解答题 ‎1、（昌平区2019届高三上学期期末）如图，在五面体中，四边形是边长为的正方形，平面⊥平面， .‎ ‎(Ⅰ) 求证：；‎ ‎(Ⅱ) 求证：平面⊥平面；‎ ‎(Ⅲ) 在线段上是否存在点，使得⊥平面？ 说明理由.‎ ‎2、（朝阳区2019届高三上学期期末）如图，三棱柱的侧面是平行四边形，，平面平面，且分别是的中点.‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求证：平面；‎ ‎（Ⅲ）在线段上是否存在点，使得平面？若存在，求出的值；若不存在，请说明理由.‎ ‎3、（大兴区2019届高三上学期期末）如图，正方形和梯形所在的平面互相垂直，，， 与交于点，，分别为线段，的中点． ‎ ‎（Ⅰ）求证：； ‎ ‎（Ⅱ）求证：平面；‎ ‎（Ⅲ）若，求证：平面平面．‎ ‎4、（东城区2019届高三上学期期末）如图，三棱柱 中，侧棱垂直于底面， ， ， ，为中点. ‎ ‎（I） 求证：平面 ；‎ ‎(II) 求三棱锥 的体积；‎ ‎（III） 设平面与直线交于点，求线段的长.‎ ‎5、（房山区2019届高三上学期期末）如图,在三棱柱中, ⊥底面，底面为等边三角形，‎ ‎,, ,分别为, 的中点. ‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证：平面平面；‎ ‎（Ⅲ）求四棱锥的体积.‎ ‎6、（丰台区2019届高三上学期期末）如图，在四棱柱中，底面 为正方形，侧棱底面， 为棱的中点，，．‎ ‎（Ⅰ）求证：平面； ‎ ‎（Ⅱ）求证：；‎ ‎（Ⅲ）求三棱锥的体积．‎ ‎7、（海淀2019届高三上学期期末）在四棱锥中，平面平面， 底面为梯形, ，.‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证：平面；‎ ‎（Ⅲ）若是棱的中点，求证：对于棱上任意一点，‎ 与都不平行.‎ ‎ ‎ ‎8、（石景山区2019届高三上学期期末）如图，在多面体中，已知是边长为2的正方形，为正三角形，且，，分别为的中点.‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证：平面；‎ ‎（Ⅲ）求三棱锥的体积.‎ ‎9、（通州区2019届高三上学期期末）如图，在三棱柱 中，底面，△ABC是边长为的正三角形，， E，F 分别为BC，的中点．‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求三棱锥的体积；‎ ‎（Ⅲ）在线段上是否存在一点M，使直线MF与平面没有公共点？若存在，求的值；若不存在，请说明理由.‎ ‎10、（朝阳区2019届高三第二次（5月）综合练习（二模））如图1，在直角梯形中，,, ，，,点在上，且，将沿折起，使得平面平面（如图2）.‎ ‎ 为中点.‎ ‎（Ⅰ）求证:平面；‎ ‎（Ⅱ）求四棱锥的体积；‎ ‎（Ⅲ）在线段上是否存在点，使得平面？若存在，求的值；若不存在，请说明理由.‎ ‎11、（东城区2019届高三5月综合练习（二模））如图所示的五面体中，平面平面, ,,∥，,，．‎ ‎（Ⅰ）求四棱锥的体积；‎ ‎（Ⅱ）求证：∥平面；‎ ‎（Ⅲ）设点为线段上的动点，求证：与不垂直．‎ ‎12、（丰台区2019届高三5月综合练习（二模））在菱形中，，为线段的中点（如图1）．将沿折起到的位置，使得平面平面，为线段的中点（如图2）．‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求证：平面；‎ ‎（Ⅲ）当四棱锥的体积为时，求的值．‎ ‎ 图1 图2‎ ‎13、（海淀区2019届高三5月期末考试（二模））如图1所示，在等腰梯形，∥，，垂足为，，.将沿折起到的位置，‎ 使平面平面，如图2所示，点为棱的中点。‎ ‎ (Ⅱ) 求证：∥平面；‎ ‎(Ⅱ)求证：平面；‎ ‎(Ⅲ)求三棱锥 的体积．‎ ‎14、（海淀区2019届高三一模）如图，在三棱柱中，平面,，点分别为棱的中点．‎ ‎(Ⅱ)求证：∥平面 ‎(Ⅱ)求证：平面平面;‎ ‎(Ⅲ)求三棱锥的体积.‎ ‎15、（门头沟区2019届高三一模）在四棱锥中，底面是边长为6的菱形，且，，是棱上的一动点，为的中点.‎ ‎（Ⅰ）求此三棱锥的体积；‎ ‎（Ⅱ）求证：平面 ‎（Ⅲ）若，侧面内是否存在过点的一条直线，使得直线上任一点都 有平面，若存在，给出证明，若不存在，请明理由.‎ ‎16、（顺义区2019届高三第二次统练（一模））如图，平面，，，，为棱上一点，平面与棱交于点.‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证：；‎ ‎（Ⅲ）当四边形为矩形时，求四棱锥的体积.‎ ‎17、（西城区2019届高三一模）如图，在多面体中，底面为矩形，侧面为梯形，，，. ‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求证：平面； ‎ ‎（Ⅲ）判断线段上是否存在点，使得平面平面？并说明理由．‎ 参考答案：‎ ‎1、证明：(Ⅰ) 在五面体中，因为四边形是正方形，‎ ‎ 所以.‎ 因为平面,平面，‎ 所以平面. ……4分 ‎(Ⅱ) 因为,，‎ 所以，所以，即.‎ 因为四边形是正方形，所以.‎ 因为平面⊥平面，平面平面， ‎ 所以⊥平面.‎ 因为,所以 ⊥.‎ 因为 所以⊥平面 因为， 所以平面⊥平面. ……9分 ‎(Ⅲ)在线段上存在点，使得⊥平面 证明如下：‎ 取的中点，连接.‎ 由（Ⅰ）知, ,‎ ‎,‎ 所以.‎ 因为 所以.‎ 所以四边形是平行四边形.‎ 所以.‎ 由(Ⅱ)知，⊥平面，‎ 所以. ………………………14分 ‎2、（Ⅰ）因为，又平面平面，‎ 且平面平面，‎ 所以平面.‎ 又因为平面，‎ 所以. …………………4分 ‎（Ⅱ）取中点，连连.‎ 在△中，因为分别是中点，‎ 所以，且.‎ 在平行四边形中，因为是的中点，‎ 所以，且.‎ 所以，且.‎ 所以四边形是平行四边形.‎ 所以.‎ 又因为平面，平面，所以平面.‎ ‎…………………9分 ‎（Ⅲ）在线段上存在点，使得平面.‎ 取的中点，连，连.‎ 因为平面，平面,平面,‎ 所以,.‎ 在△中，因为分别是中点，所以.‎ 又由（Ⅱ）知，‎ 所以，.‎ 由得平面.‎ ‎ 故当点是线段的中点时，平面.此时，.‎ ‎…………………14分 ‎3、解：（Ⅰ）因为为正方形，所以． ……1分 ‎ 又因为平面平面，‎ 平面平面，‎ 所以平面． ……3分 又因为平面，‎ 所以． ……4分 ‎（Ⅱ）方法一：取中点，连接，，‎ 在中，，分别为，的中点，‎ 所以且． ……1分 又因为且，‎ 所以且 ． ……2分 所以四边形为平行四边形.‎ 所以. ……3分 因为平面，‎ 平面， ……4分 所以平面． ……5分 方法二： ‎ 连接，，‎ 因为且，‎ 所以且.‎ 所以四边形为平行四边形． ……1分 所以．‎ 因为平面，‎ 平面，‎ 所以平面． ……2分 因为，分别为，的中点，‎ 所以． ‎ 又因为平面， 平面，‎ 所以平面． ……3分 因为，‎ 所以平面平面． ……4分 因为平面，‎ 所以平面． ……5分 ‎（Ⅲ）连接，‎ 在中，，分别为，的中点，‎ 所以. ……1分 因为，‎ 所以. ……2分 因为，‎ ‎，‎ 平面，平面，‎ 所以平面. ……4分 因为平面，‎ 所以平面平面． ……5分 ‎4、解：（Ⅰ）因为三棱柱 中，侧棱垂直于底面，‎ ‎ 所以平面.‎ 因为平面，‎ 所以.‎ 又因为，，‎ 所以平面 .‎ 因为平面，‎ 所以.‎ 因为，所以四边形为菱形.‎ 所以.‎ 因为，‎ 所以平面. ……………………………..5分 ‎（Ⅱ） 由已知，平面，平面，‎ 所以 .‎ 因为， ，‎ 所以 平面.‎ 又，故 到平面的距离为.‎ 因为为中点，所以点到平面距离为.‎ 所以．……..9分 ‎（Ⅲ）在三棱柱中，‎ 因为，为平面与平面的公共点， ‎ 所以平面平面.‎ 因为平面平面，平面，‎ 所以平面.‎ 又平面平面, ‎ 所以.‎ 又，所以.‎ 因为为中点, 所以为中点 .‎ 所以．………………………..14分 ‎5、‎ ‎6、解：（Ⅰ）设， 连接， ‎ 因为 中，，分别为，的中点，‎ 所以 为的中位线，即， ………………2分 因为 平面，平面，‎ 所以 平面． ………………4分 ‎（Ⅱ）因为 侧棱底面，底面，‎ 所以 ， ………………5分 因为 底面为正方形，‎ 所以 ， ………………6分 因为 ， ‎ 所以 平面， ……………… 8分 因为 平面， ‎ 所以 ． ………………10分 ‎（Ⅲ）因为 侧棱底面于，为棱的中点，‎ 所以为三棱锥的高.‎ 因为，‎ 所以.‎ 因为，‎ 所以. ‎ 所以， ………………14分 ‎7、证明：‎ ‎（Ⅰ）因为 ‎ 平面 ‎ 平面 ‎ 所以平面 ‎ ‎（Ⅱ）法一：‎ 因为平面平面 平面平面 ‎ ‎,平面 ‎ 所以平面 ‎ 法二：‎ 在平面中过点作，交于 因为平面平面 平面平面 平面 所以平面 ‎ 因为平面 所以 又，‎ 所以平面 ‎ ‎（Ⅲ）法一：‎ 假设存在棱上点，使得 ‎ 连接，取其中点 在中，因为分别为的中点，所以 ‎ 因为过直线外一点只有一条直线和已知直线平行，所以与重合 所以点在线段上，所以是，的交点 即就是 而与相交，矛盾，所以假设错误，问题得证 ‎ 法二：‎ 假设存在棱上点，使得，显然与点不同 ‎ 所以四点在同一个平面中 ‎ 所以，‎ 所以，‎ 所以就是点确定的平面 ，且 这与为四棱锥矛盾，所以假设错误，问题得证 ‎ ‎8、‎ ‎（Ⅰ）证明：取的中点，连结， ‎ ‎ ∵四边形是边长为的正方形，为的中点，‎ ‎ ∴，‎ ‎ ∵为的中点，且，‎ ‎ ∴，又∥，‎ ‎ ∴，‎ ‎ ∴四边形为平行四边形， ‎ ‎ ∴， ‎ 又平面，平面，‎ ‎∴∥平面． ‎ ‎（Ⅱ）证明：∵∥，，‎ ‎ ∴，‎ ‎ 在正方形中，且，‎ ‎ ∴平面， ‎ ‎ ∵平面，‎ ‎ ∴， ‎ ‎ 又为正三角形，为的中点，‎ ‎ ∴‎ ‎ 又 ‎ ∴平面． ‎ ‎（Ⅲ）∵∥，‎ ‎ ∴∥平面，‎ ‎ ∵平面，‎ ‎ ∴为三棱锥的高， ‎ ‎ ∵为正三角形，为的中点，‎ ‎ ∴，‎ ‎ ∴． ‎ ‎9、（Ⅰ）证明：在三棱柱中，‎ 因为△ABC为等边三角形，E为BC中点，‎ 所以AE⊥BC．　　　　　　　　　　　 ……………………………… ………………1分 又平面，AE⊂平面ABC，所以．‎ 因为，所以．　　　　 ……………………………………………2分 因为，平面，平面，‎ 所以． 　　　　　　…………………………………………………3分 所以平面平面； 　　　…………………………………………………4分 ‎（Ⅱ）解： ………………5分 取的中点，连结，则 ，，‎ 所以，．　………………6分 又是的中点，所以，．…………………………………7分 ‎ 所以，‎ 即三棱锥的体积为．………………9分 ‎（Ⅲ）解：在上存在一点M，满足题意.‎ 取中点M，连结MF． ………………10分 因为是的中点， ‎ 所以MF是的中位线，‎ 所以． ………………………………………………………………11分 因为平面，平面，‎ 所以平面， ………………………………………………12分 即直线MF与平面没有公共点． ………………………………………………13分 所以．　　　　　 ………………………………………………………………14分 ‎10、‎ 解： （Ⅰ）证明：‎ 因为为中点，，‎ ‎ 所以.‎ 因为平面平面，‎ 平面平面，平面， ‎ 所以平面． ………….4分 ‎（Ⅱ）在直角三角形中，易求,则．‎ 所以四棱锥的体积的体积为 ‎． …………8分 ‎ ‎（Ⅲ） 过点作交于点，则． ‎ 过点作交于点，连接,则．‎ 又因为， 平面,平面,‎ P F E D C B A 所以平面．‎ 同理平面．‎ 又因为，‎ 所以平面平面．‎ 因为平面 ， ‎ 所以平面．‎ 所以在上存在点，使得平面，且．‎ ‎ ………….13分 ‎ ‎11、‎ 解：（Ⅰ）取中点，连接．‎ ‎ 在△中，， ‎ ‎ 所以.‎ 因为平面平面，‎ 平面平面，‎ 平面,‎ ‎ 所以平面．‎ 又因为，，所以.‎ 因为∥，，，，‎ 所以.‎ 所以. …………….5分 ‎（Ⅱ）因为∥，平面，平面，‎ ‎ 所以∥平面．‎ 又因为平面，平面平面，‎ 所以∥．‎ 因为平面，平面，‎ 所以∥平面．…………….10分 ‎（Ⅲ）连接，假设.‎ 由（Ⅰ）知平面，‎ ‎ 因为平面,所以．‎ 因为, 且， ‎ ‎ 所以平面．‎ ‎ 因为平面，‎ ‎ 所以．‎ ‎ 在△中，，‎ ‎ 所以.‎ ‎ 所以．‎ ‎ 这与矛盾．‎ ‎ 所以假设不成立，即与不垂直．…………….14分 ‎12、解：（Ⅰ）证明：因为在菱形中，，为线段的中点，‎ 所以． ………………1分 因为平面平面，‎ 平面平面，‎ 平面，‎ 所以平面． ………………4分 因为平面，‎ 所以． ………………5分 ‎（Ⅱ）证明：如图，取为线段的中点，连接，；‎ ‎ 因为在中，，分别是线段，的中点，‎ 所以，． ‎ ‎ 因为是线段的中点，菱形中，，，‎ ‎ 所以．‎ ‎ 所以，． ………………6分 ‎ 所以，．‎ ‎ 所以四边形为平行四边形， ………………7分 ‎ 所以，‎ ‎ 因为平面，平面，‎ ‎ 所以平面； ………………10分 ‎（Ⅲ）解：由（Ⅰ）知平面．‎ ‎ 所以是四棱锥的高． ………………11分 ‎ 因为，‎ ‎ 所以． ………………14分 ‎13、解：（Ⅰ）方法1：‎ 在图1的等腰梯形内，过作的垂线，垂足为，‎ ‎ 因为，所以 ‎ 又因为 ，，‎ 所以四边形为正方形，‎ 且，为中点 ‎ ‎ 在图2中，连结 ‎ 因为点是的中点， ‎ ‎ 所以 ‎ ‎ 又因为，，‎ 平面， 平面， ‎ ‎ 所以平面平面 ‎ ‎ 又因为 ，所以平面 ‎ 方法2：‎ 在图1的等腰梯形内，过作的垂线，垂足为 ‎ ‎ 因为，所以 ‎ 又因为 ，，‎ 所以四边形为正方形，为中点 ‎ ‎ 在图2中，连结 ‎ 因为点是的中点，‎ ‎ 所以 ‎ ‎ 又平面，平面 ‎ 所以平面 ‎ ‎ 又因为，平面，平面 ‎ 所以平面 ‎ 又因为 ‎ 所以平面平面 ‎ ‎ 又因为 ，所以平面 ‎ 方法3：‎ 在图1的等腰梯形内，过作的垂线，垂足为，‎ ‎ 因为，所以 ‎ 又因为 ，，‎ 所以四边形为正方形，，得 ‎ 所以 ‎ 在图2中设点为线段的中点，连结，‎ ‎ 因为点是的中点，‎ ‎ 所以 ‎ 所以，所以四边形为平行四边形 ‎ 所以 ‎ 又因为平面，平面 所以平面 ‎ ‎（Ⅱ） 因为平面平面，‎ 平面平面,‎ 平面，‎ 所以平面 ‎ 又因为平面 所以 ‎ 又，满足 ，‎ 所以 ‎ 又 ‎ 所以平面 ‎ ‎（Ⅲ），‎ ‎ 所以 ‎ 线段为三棱锥底面的高 ‎ ‎ 所以 ‎ ‎14、解：（I）证明：因为三棱柱中，‎ ‎ 又因为分别为的中点，所以 ‎ 于是 ‎ ‎ 平面，平面 ‎ 所以平面 ‎ ‎(II) 在三棱柱中，‎ 平面，平面，平面 所以， ‎ 又 ‎，平面 所以平面 ‎ 平面 所以 ‎ 又因为， ，‎ 所以侧面为正方形，故 ‎ 而分别为的中点，连结，所以‖‎ 所以 ，又，平面 所以平面 ‎ 又平面 所以平面平面 ‎ ‎（Ⅲ） ‎ ‎ ‎ ‎15、解：（Ⅰ）由题意可知，，‎ ‎（Ⅱ）由题意可知，，‎ 则，又底面是菱形，‎ ‎，所以，，‎ 平面 ‎（Ⅲ）设是的中点，连结，‎ 则 所以直线上任一点都满足平面.‎ ‎16、（Ⅰ）证明：因为 ‎ 所以--------------------------------2分 因为平面，平面 所以--------------------------------2分 因为 所以平面.-------------------------5分 ‎（Ⅱ）证明：因为，平面，平面 所以平面--------------------------7分 因为平面，平面平面= ‎ 所以.------------------9分 ‎（Ⅲ））解：因为，‎ 所以 当四边形为矩形时,‎ 所以为的中位线，-------------------------10分 ‎ 因为平面 所以，‎ 所以，‎ 此时四边形为矩形，‎ 又，‎ 所以平面 ---------------------------12分 所以 --------------14分 ‎17、解：（Ⅰ）由底面为矩形，知. ……………… 1分 ‎ 又因为，， ……………… 2分 ‎ ‎ 所以平面. ……………… 3分 ‎ ‎ 又因为平面，‎ ‎ 所以. ……………… 4分 D A B C E F P Q ‎ （Ⅱ）由底面为矩形，知，‎ ‎ 又因为平面，平面， ‎ ‎ 所以平面. ……………… 6分 ‎ 同理平面，‎ ‎ 又因为，‎ ‎ 所以平面平面. ……………… 8分 ‎ 又因为平面，‎ ‎ 所以平面. ……………… 9分 ‎ （Ⅲ）结论：线段上存在点（即的中点），使得平面平面. … 10分 ‎ 证明如下：‎ ‎ 取的中点，的中点，连接，则.‎ ‎ 由，得. ‎ ‎ 所以四点共面. ……………… 11分 ‎ 由（Ⅰ），知平面，‎ ‎ 所以，故.‎ ‎ 在△中，由，可得. ‎ ‎ 又因为，‎ ‎ 所以平面. ……………… 13分 ‎ 又因为平面 ‎ 所以平面平面（即平面平面）. ‎ ‎ 即线段上存在点（即中点），使得平面平面. ……… 14分 ‎