- 2021-06-20 发布 |
- 37.5 KB |
- 13页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年高考数学(理)二轮复习讲练测 专题21 几何体与球切、接的问题(讲)(解析版)
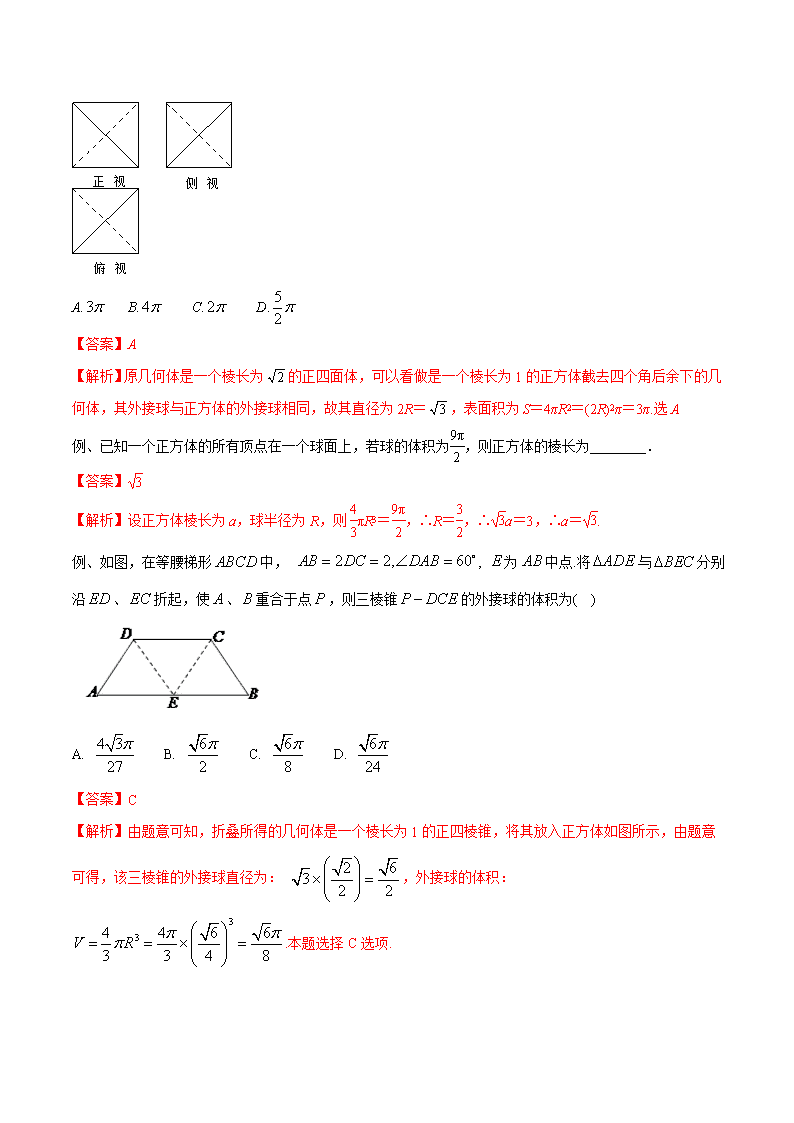
专题21 几何体与球切、接的问题 纵观近几年高考对于组合体的考查,与球相关的外接与内切问题是高考命题的热点之一.高考命题小题综合化倾向尤为明显,要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识学生掌握较为薄弱、认识较为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理. 下面结合近几年高考题对球与几何体的切接问题作深入的探究,以便更好地把握高考命题的趋势和高考的命题思路,力争在这部分内容不失分.从近几年全国高考命题来看,这部分内容以选择题、填空题为主,大题很少见. 首先明确定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。 定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球. 1 球与柱体的切接 规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题. 1.1 球与正方体 如图所示,正方体,设正方体的棱长为,为棱的中点,为球的球心.常见组合方式有三类:一是球为正方体的内切球,截面图为正方形和其内切圆,则;二是与正方体各棱相切的球,截面图为正方形和其外接圆,则;三是球为正方体的外接球,截面图为长方形和其外接圆,则 .通过这三种类型可以发现,解决正方体与球的组合问题,常用工具是截面图,即根据组合的形式找到两个几何体的轴截面,通过两个截面图的位置关系,确定好正方体的棱与球的半径的关系,进而将空间问题转化为平面问题. (1)正方体的内切球,如图1. 位置关系:正方体的六个面都与一个球都相切,正方体中心与球心重合; 数据关系:设正方体的棱长为,球的半径为,这时有. (2)正方体的外接球,如图2. 位置关系:正方体的八个顶点在同一个球面上;正方体中心与球心重合; 数据关系:设正方体的棱长为,球的半径为,这时有. (3)正方体的棱切球,如图3. 位置关系:正方体的十二条棱与球面相切,正方体中心与球心重合; 数据关系:设正方体的棱长为,球的半径为,这时有. 例. 某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( ) 俯视图 正视图 侧视图 A. B. C. D. 【答案】A 【解析】原几何体是一个棱长为的正四面体,可以看做是一个棱长为1的正方体截去四个角后余下的几何体,其外接球与正方体的外接球相同,故其直径为2R=,表面积为S=4πR2=(2R)2π=3π.选A 例、已知一个正方体的所有顶点在一个球面上,若球的体积为,则正方体的棱长为________. 【答案】 【解析】设正方体棱长为a,球半径为R,则πR3=,∴R=,∴a=3,∴a=. 例、如图,在等腰梯形中, , 为中点.将与分别沿、折起,使、重合于点,则三棱锥的外接球的体积为( ) A. B. C. D. 【答案】C 【解析】由题意可知,折叠所得的几何体是一个棱长为1的正四棱锥,将其放入正方体如图所示,由题意可得,该三棱锥的外接球直径为: ,外接球的体积: .本题选择C选项. 1.1 球与长方体 例、如图所示是一个几何体的三视图,则这个几何体外接球的表面积为( ) A.8π B.16π C.32π D.64π 【答案】C 【解析】还原三视图可知该几何体为一个四棱锥,将该四棱锥补成一个长、宽、高分别为2,2,4的长方体,则该长方体外接球的半径r==2,则所求外接球的表面积为4πr2=32π. 例 、【广东省佛山市2020届高三月考】已知矩形,,,为的中点,现分别沿将,翻折,使点重合,记为点,则几何体的外接球表面积为______. 【答案】 【解析】由AB=1,AD=,E为AD中点,可得PE=,PB=PC=1,得 ∠EPB=∠EPC=90°,∠CPB=90°,∴P﹣BCE为长方体一角,其外接球直径为其体对角线长,∴,∴,∴外接球表面积为4πR2=,故答案为:. 例、《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥PABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥PABC的四个顶点都在球O的球面上,则球O的表面积为( ) A. 8π B. 12π C. 20π D. 24π 【答案】C 【解析】将三棱锥PABC放入长方体中,如图,三棱锥PABC的外接球就是长方体的外接球.因为PA=AB=2,AC=4,△ABC为直角三角形,所以BC==2.设外接球的半径为R,依题意可得(2R)2=22+22+(2)2=20,故R2=5,则球O的表面积为4πR2=20π.故选C. 1.1 球与正三棱柱 例、直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上”,若AB=3,AC=4,AB⊥AC,AA1=12,求球O的半径。 【答案】。 【解析】设球的半径为R,因为直三棱柱中AB=3,AC=4,AA1=12,AB⊥AC,所以BC=5,且BC为过底面ABC的截面圆的直径。取BC中点D,则OD⊥底面ABC,则O在侧面BCC1B1内,矩形BCC1B1的对角线长即为球直径,所以2R==13,即R=。 例、已知正三棱柱ABC-A1B1C1的所有顶点都在半径为1的球面上,当正三棱柱的体积最大时,该正三棱柱的高为________。 【答案】 【解析】作出正三棱柱ABC-A1B1C1如图所示,由题意知,球心O为两底面ABC,A1B1C1的中心O1,O2的连线的中点,设三棱柱的高O1O2=h,因为球的半径OC=1,所以在Rt△OO2C中,有O2C=,所以CD=O2C,AB=CD=O2C,所以VABC-A1B1C1=·AB·CD·O1O2=×××·h=(-h3+4h),易知当h=时,三棱柱的体积取得最大值。 2 球与锥体的切接 规则的锥体,如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱锥的棱和高产生联系,然后考查几何体的体积或者表面积等相关问题. 2.1正四面体与球的切接问题 (1) 正四面体的内切球,如图4. 位置关系:正四面体的四个面都与一个球相切,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为,高为;球的半径为,这时有;(可以利用体积桥证明) (2) 正四面体的外接球,如图5. 位置关系:正四面体的四个顶点都在一个球面上,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为,高为;球的半径为,这时有;(可用正四面体高减去内切球的半径得到) (3) 正四面体的棱切球,如图6. 位置关系:正四面体的六条棱与球面相切,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为,高为;球的半径为,这时有 例、若一个正四面体的表面积为S1,其内切球的表面积为S2,则=________. 【答案】. 【解析】设正四面体棱长为a,则正四面体表面积为S1=4··a2=a2,其内切球半径为正四面体高的,即r=·a=a,因此内切球表面积为S2=4πr2=,则==. 例、【吉林省长春外国语学校2020届高三上期末】在四面体中,若,,,则四面体的外接球的表面积为__________. 【答案】 【解析】由题意可采用割补法,考虑到四面体ABCD的四个面为全等的三角形,所以可在其每个面补上一个以,2,为三边的三角形作为底面,且以分别x,y,z 长、两两垂直的侧棱的三棱锥,从而可得到一个长、宽、高分别为x,y,z的长方体,并且x2+y2=3,x2+z2=5,y2+z2=4,则有(2R)2=x2+y2+z2=6(R为球的半径),得2R2=3,所以球的表面积为S=4πR2=6π.故答案为:. 点评:与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图. 一般外接球需要求球心和半径,首先应确定球心的位置,借助于外接球的性质,球心到各顶点距离相等,这样可先确定几何体中部分点组成的多边形的外接圆的圆心,过圆心且垂直于多边形所在平面的直线上任一点到多边形的顶点的距离相等,然后同样的方法找到另一个多边形的各顶点距离相等的直线(这两个多边形需有公共点),这样两条直线的交点,就是其外接球的球心,再根据半径,顶点到底面中心的距离,球心到底面中心的距离,构成勾股定理求解,有时也可利用补体法得到半径. 2.2其它棱锥与球的切接问题 球与正棱锥的组合,常见的有两类,一是球为三棱锥的外接球,此时三棱锥的各个顶点在球面上,根据截面图的特点,可以构造直角三角形进行求解.二是球为正棱锥的内切球,例如正三棱锥的内切球,球与正三棱锥四个面相切,球心到四个面的距离相等,都为球半径.这样求球的半径可转化为球球心到三棱锥面的距离,故可采用等体积法解决,即四个小三棱锥的体积和为正三棱锥的体积. 球与一些特殊的棱锥进行组合,一定要抓住棱锥的几何性质,可综合利用截面法、补形法等进行求解.例如,四个面都是直角三角形的三棱锥,可利用直角三角形斜边中点几何特征,巧定球心位置. 例、【山东省临沂市第十九中学2020届高三调研】长方形中,,将沿折起,使二面角大小为,则四面体的外接球的表面积为________ 【答案】 【解析】如图所示:设矩形ABCD的对角线AC、BD交于点O,则OA=OB=OC=OD=,∴三棱锥B-ACD的外接球的半径为R=,其表面积为S=4πR2=4π•=. 故答案为. 例、【甘肃省张掖市2020届高三考】三棱锥的每个顶点都在球的表面上,平面,,,,,则球的表面积为_____. 【答案】 【解析】∵平面,则PA⊥BC,且,则平面,所以PA⊥AC,又,∴PC为三棱锥外接球的直径,∴, ∴PC的中点为球O的球心,∴球O的半径r=,∴球O的面积S=4πr2=8π.故答案为:8π. 例、【广东省深圳市高级中学2020届高三适应性考试】在三棱锥中,平面平面,是边长为6的等边三角形,是以为斜边的等腰直角三角形,则该三棱锥外接球的表面积为_______. 【答案】 【解析】如图,在等边三角形中,取的中点,设等边三角形的中心为,连接PF,CF,OP.由,得,是以为斜边的等腰角三角形,,又平面平面,平面, ,, 则为棱锥的外接球球心,外接球半径, 该三棱锥外接球的表面积为,故答案为. 【名师点睛】本题主要考查四面体外接球表面积,考查空间想象能力,是中档题. 要求外接球的表面积和体积,关键是求出球的半径.求外接球半径的常见方法有:①若三条棱两两垂直,则用(为三条棱的长);②若面(),则(为外接圆半径);③ 可以转化为长方体的外接球;④特殊几何体可以直接找出球心和半径. 3 球与球相切问题 对于球与球的相切组合成复杂的几何体问题,要根据丰富的空间想象力,通过准确确定各个小球的球心的位置,或者巧借截面图等方法,将空间问题转化平面问题求解. 例、已知有半径分别为2、3的球各两个,且这四个球彼此相外切,现有一个球与此四个球都相外切,则此球 的半径为 . 【答案】 【解析】如图:设四个球的球心分别为A、B、C、D,则AD=AC=BD=BC=5,AB=6,CD=4.设AB中点为E、CD中点为F,连结EF.在△ABF中求得BF=,在△EBF中求得EF=. 由于对称性可得第五个球的球心O在EF上,连结OA、OD.设第五个 球的半径为r,则OA=r+3,OD=r+2,于是OE=, OF=,∵OE+OF=EF, ∴平方整理再平方得解得或(舍掉),故答案为. 例、 把四个半径都是1的球中的三个放在桌面上,使它两两外切,然后在它们上面放上第四个球,使它与 前三个都相切,求第四个球的最高点与桌面的距离. 【答案】. 【解析】四球心组成棱长为2的正四面体的四个顶点,则正四面体的高. 而第四个球的最高点到第四个球的球心距离为求的半径1,且三个球心到桌面的距离都为1,故第四 个球的最高点与桌面的距离为. 4 球与几何体的各条棱相切问题 球与几何体的各条棱相切问题,关键要抓住棱与球相切的几何性质,达到明确球心的位置为目的,然后通过构造直角三角形进行转换和求解.如与正四面体各棱都相切的球的半径为相对棱的一半:. 例、 把一个皮球放入如图10所示的由8根长均为20 cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都有接触点,则皮球的半径为( ) A.l0cm B.10 cm C.10cm D.30cm 【答案】B 【解析】如图所示,由题意球心在AP上,球心为O,过O作BP的垂线ON垂足为N,ON=R,OM=R, 因为各个棱都为20,所以AM=10,BP=20,BM=10,AB=,设, 在BPM中,,所以. 在PAM中, ,所以. 在ABP中, , 在ONP中, ,所以,所以. 在OAM中, ,所以,,解得,或30(舍), 所以,故选B. 4 球与旋转体切接问题 首先画出球及其它旋转体的公共轴截面,然后寻找几何体与几何体几何元素之间的关系. 例、【山东省滨州市2020届高三期末】如图,圆柱的底直径与高都等于球的直径,记圆柱的表面积为,球的表面积为,则( ) A.1 B. C. D. 【答案】C 【解析】设球的半径为,则球的表面积为,可得圆柱的底面半径为,高为, 圆柱的表面积为,则,故选C. 例、在棱长为1的正方体内有两个球相外切且又分别与正方体内切.(1)求两球半径之和;(2)球的半径 为多少时,两球体积之和最小. 【解析】如图,球心和在上,过,分别作的垂线交于.则由得. ,. (1)设两球体积之和为,则 ==,当时,有最小值.当时,体积之和有最小值. 【反思提升】综合上面的五种类型,解决与球的外切问题主要是指球外切多面体与旋转体,解答时首先要找准切点,将问题转化成平面几何问题,应用三角形中的边角关系,建立与球半径的联系,将球的体积之和用或表示.如果外切的是多面体,则作截面时主要抓住多面体过球心的对角面来作;把一个多面体的几个顶点放在球面上即为球的内接问题.解决这类问题的关键是抓住内接的特点,即球心到多面体的顶点的距离等于球的半径.发挥好空间想象力,借助于数形结合进行转化,问题即可得解.如果是一些特殊的几何体,如正方体、正四面体等可以借助结论直接求解,此时结论的记忆必须准确.高考题往往与三视图相结合,题目的难易不一,在复习中切忌好高骛远,应重视各种题型的备考演练,重视高考信息的搜集,不断充实题目的类型,升华解题的境界.查看更多