浙江省超级全能生2020届高三选考科目9月联考（B） 数学 （缺第20题）

浙江省超级全能生2020届高三选考科目9月联考（B） 数学 （缺第20题）

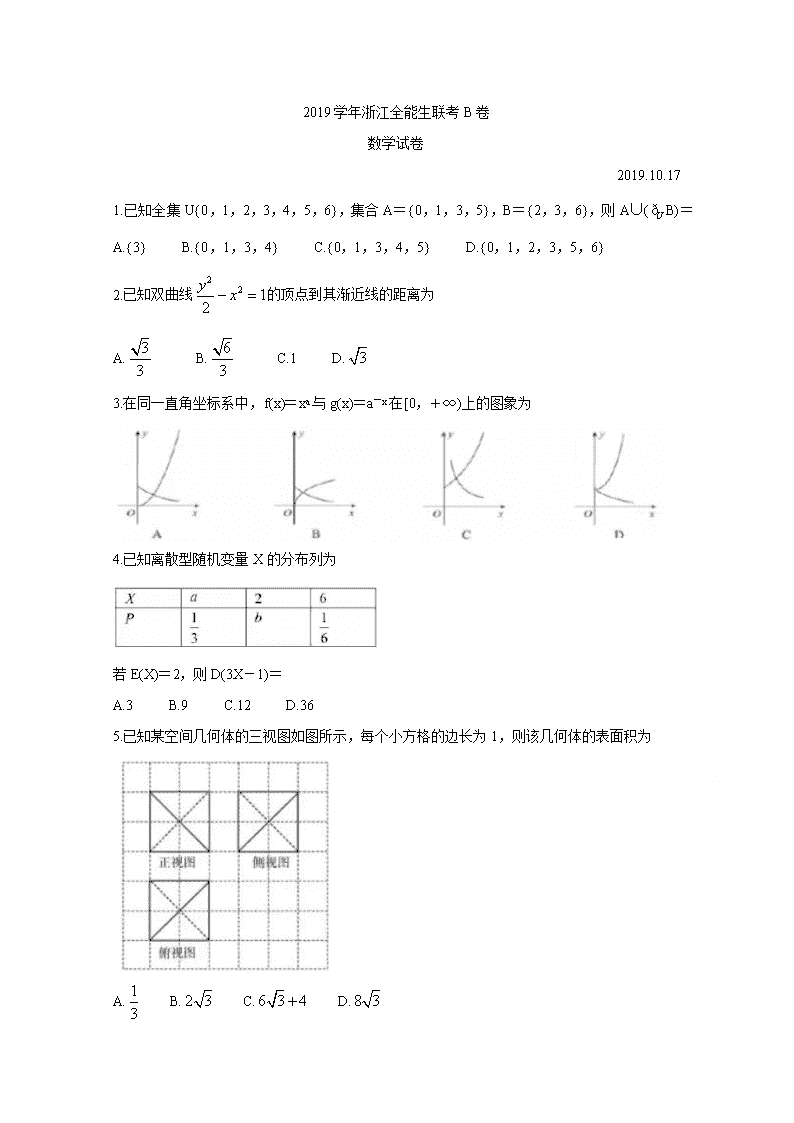
‎2019学年浙江全能生联考B卷 数学试卷 ‎2019.10.17‎ ‎1.已知全集U{0，1，2，3，4，5，6}，集合A＝{0，1，3，5}，B＝{2，3，6}，则A∪(B)＝‎ A.{3} B.{0，1，3，4} C.{0，1，3，4，5} D.{0，1，2，3，5，6}‎ ‎2.已知双曲线的顶点到其渐近线的距离为 A. B. C.1 D. ‎ ‎3.在同一直角坐标系中，f(x)＝xa与g(x)＝a－x在[0，＋∞)上的图象为 ‎4.已知离散型随机变量X的分布列为 若E(X)＝2，则D(3X－1)＝‎ A.3 B.9 C.12 D.36‎ ‎5.已知某空间几何体的三视图如图所示，每个小方格的边长为1，则该几何体的表面积为 A. B. C. D.‎ ‎6.已知函数f(x)＝sinx，x∈[0，2π)，则“f(r)≥0”是“f(x2)≥0”的 A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 ‎7.设z＝－x＋2y，其中x，y满足，若z的最大值为11，则实数c＝‎ A.21 B.22 C.23 D.24‎ ‎8.在三棱柱ABC－A1B1C1中，E，F分别是AC1，B1C的中点，P为该三棱柱表面上一动点，若此三棱柱恰好有5条棱与平面PEF平行，则动点P的轨迹为除去E，F两点的 A.线段 B.三角形，且其所在平面平行于平面AA1C1C C.梯形，且其所在平面平行于平面BB1C1C D.平行四边形，且其所在平面平行于平面AA1B1B ‎9.若直线MN过△ABC的重心G，且，，其中m>0，n>0，则m＋2n的最小值是 A. B. C.2 D.‎ ‎10.设数列{an}的前n项积为Tn＝1－an，记Sn＝T12＋T22＋…＋Tn2，则Sn－an＋1的取值范围为 A. B. C. D.‎ ‎11.若复数(i为虚数单位)，则|z|＝ ，z的共轭复数＝ 。‎ ‎12.公元前3世纪，古希腊数学家阿波罗尼斯对圆锥曲线有深刻的研究，其主要成果集中于他的代表作《圆锥曲线》一书，其中有如下结果；平面内到两定点距离之比等于常数(该常数大于零且不等于1)的点的轨迹为圆，后世把这种圆称为阿波罗尼斯圆。已知在平面直角坐标系 xOy中，A(－1，0)，B(2，0)，动点P满足|PA|＝2|PB|，由上面的结果易知点P的轨迹是圆，则该圆的半径是 ，|PA|的最大值是 。‎ ‎13.若二项式的展开式中常数项为10，则实数a＝ ，展开式中所有理项的系数之和 。‎ ‎14.己知α，β为锐角，且，则cos2α＝ ，tan(a＋β)＝ 。‎ ‎15.若6把椅子摆成一排，3人随机就座，则有且仅有两人相邻的坐法有种 (用数字填空)。‎ ‎16.已知过椭圆E：的左焦点F的直线l交E于A，B两点，则|AF|＋2|BF|的最小值为 。‎ ‎17.若函数与g(x)＝4＋ax＋b(a，b∈R)的图象有交点，则a2＋b2的最小值为 。‎ ‎18.己知函数f(x)＝sin2x－cos2x－2sinxcosx，x∈[－]。‎ ‎(1)求的值；‎ ‎(2)求f(x)的最小正周期及单调递减区间。‎ ‎19.如图，在四棱锥P－ABCD中，AB⊥平面PAD，AB//DC，E为线段PD的中点。己知PA＝AB＝AD＝CD＝2，∠PAD＝120°。‎ ‎(1)证明：直线PB//平面ACE；‎ ‎(2)求直线PB与平面PCD所成角的正弦值。‎ ‎21.(本小题满分15分)如图，已知M是抛物线C：y2＝2px(p>0)上一点，直线AM，BM的斜率互为相反数，与抛物线C分别交于A，B两点，且均在M点的下方。‎ ‎(I)证明：直线AB的斜率为定值；‎ ‎(II)求△MAB面积的最大值。‎ ‎22.己知函数f(x)＝－ln(ax＋1)，其中a>0。‎ ‎(1)若0

查看更多