- 2021-06-20 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2018届山东省沂水县第一中学高三下学期第1次模拟(2018
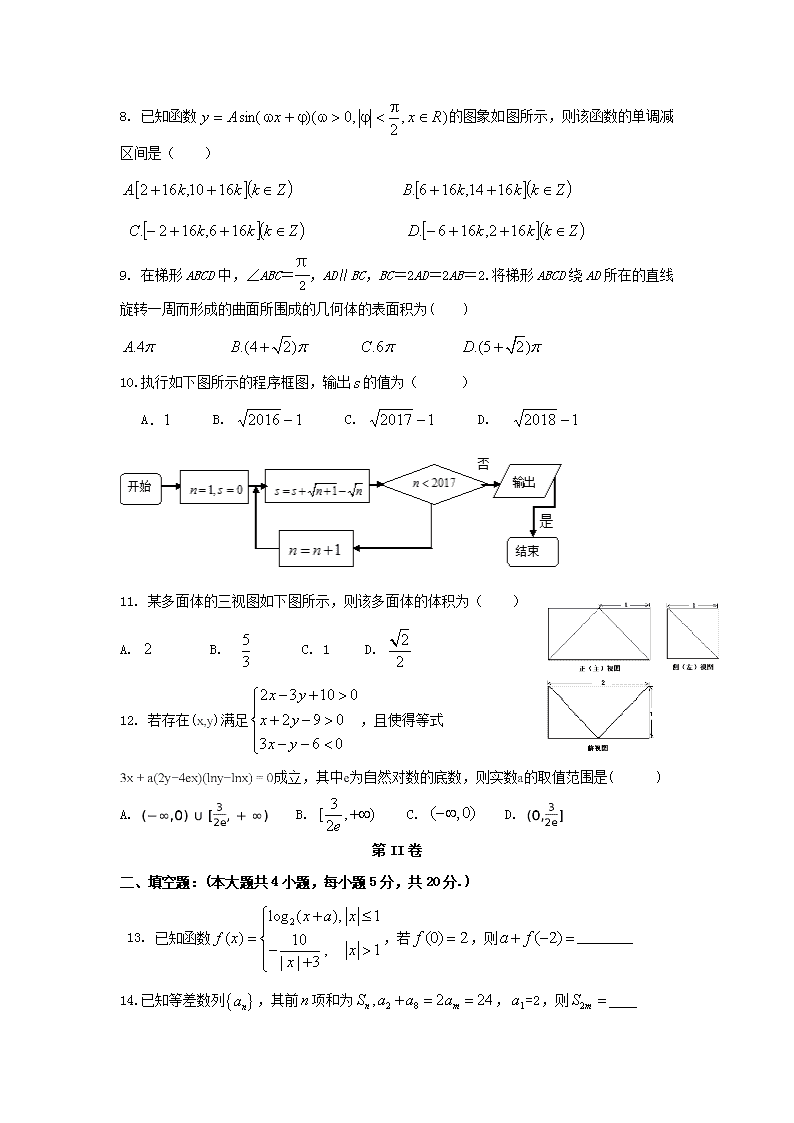
2018高三数学模拟试题(文) 第I卷 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1. 若集合,则的子集个数为( ) A.2 B.3 C.4 D.16 2. 已知点A(0,1),B(3,2),向量=(-7,-4),则向量=( ) A.(-4,-3) B.(10,5) C.(-1,4) D.(3,4) 3. 已知为虚数单位,复数满足,则( ) A. B. C. D. 4. 有5张卡片(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5张卡片中任取2张不同颜色的卡片,则取出的2张卡片中含有红色卡片的概率为( ) A. B. C. D. 5.已知点在以原点为顶点、以坐标轴为对称轴的抛物线上,抛物线的焦点为,准线为,过点作的垂线,垂足为,若,的面积为,则焦点到准线的距离为( ) A. B. C. D. 6.已知偶函数在上是增函数.若,则的大小关系为( ) A. B. C. D. 7. 《九章算术》中的 “两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”现有墙厚5尺,如下说法:①小鼠第二天穿垣半尺;②两鼠相遇需四天;③若大鼠穿垣两日卒,则小鼠至死方休.则以上说法错误的个数是( )个 A. 0 B.1 C. 2 D.3 8. 已知函数的图象如图所示,则该函数的单调减区间是( ) 9. 在梯形ABCD中,∠ABC=,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( ) 10.执行如下图所示的程序框图,输出的值为( ) A. B. C. D. 11. 某多面体的三视图如下图所示,则该多面体的体积为( ) A. B. C. 1 D. 12. 若存在()满足,且使得等式成立,其中为自然对数的底数,则实数的取值范围是( ) A. B. C. D. 第II卷 二、填空题:(本大题共4小题,每小题5分,共20分.) 13. 已知函数,若,则________ 14.已知等差数列,其前项和为,=2,则 15. 已知点P和点Q分别为函数与图象上的点,若有且只有一组点(P,Q)关于直线对称,则=_________ 16. 已知点为椭圆和双曲线的公共焦点,点P为两曲线的一个交点,且满足,设椭圆与双曲线的离心率分别为,则=_________. 三、解答题:(本大题共6小题,共70分,解答请写出文字说明、证明过程或演算步骤.) 17. (本小题共12分) 已知中,角所对的边分别为,且. (1)求证:; (2)求的面积. 18. (本小题共12分) 如图,在四棱锥PABCD中,底面ABCD是边长为2的正方形,平面平面. (1)求证:PB=PD; (2)若M为PD的中点,AM⊥平面PCD,求三棱锥DACM的体积. 19. (本小题共12分) 济南市某中学课外兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分別到气象局与某医院抄录了至月份每月号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料(表): 日期 月日 月日 月日 月日 月日 月日 昼夜温差 就诊人数(个) 该兴趣小组确定的研究方案是:先从这六组数据中选取组,用剩下的组数据求线性回归方程,再用被选取的组数据进行检验. (1)求选取的组数据恰好是相邻两个月的概率; (2)若选取的是月与6月的两组数据,请根据至月份的数据,求出关于的线性回归方程; (3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想. 其中回归系数公式,, 20. (本小题共12分) 已知曲线C的方程为ax2+ay2-2a2x-4y=0(a≠0,a为常数). (1)判断曲线C的形状; (2)设曲线C分别与x轴,y轴交于点A,B(A,B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断; (3)设直线l:y=-2x+4与曲线C交于不同的两点M,N,且,求a的值. 21. (本小题共12分) 已知函数. (1)若在处取到极值,求的值; (2)若在上恒成立,求的取值范围; (3)求证:当时,. 请考生从22、23题中任选一题做答, 22. (本小题共10分)选修4-4:坐标系与参数方程 以直角坐标系的原为极点,轴的正半轴为极轴建立极坐标系,且两个坐标系取相等的单位长度,已知直线的参数方程为为参数), 圆的极坐标方程为. (1)写出直线极坐标方程及圆标准方程; (2)设,直线和圆相交于两点,求的值. 23.(本小题共10分)选修4-5:不等式选讲 已知不等式的解集为. (Ⅰ)求集合; (Ⅱ)已知为集合中的最大正整数,若,且,求 2018高三数学(文)模拟试题参考答案及评分标准 1--5 CAACD 6--10 ABDDC 11-12 BB 13、 2 14、 15、 16、 2 17. 解:(1)因为,又由正弦定理得 ,即所以A为钝角, 又和B都为锐角,即;------6分 (2),则,得,--------------9分 所以. 解得: --------------11分 则-------12分 F (2)如图,因为AM⊥平面PCD, AM⊥PD,PD的中点为M,所以AP=AD=2 --------------8分 由AM⊥平面PCD,可得AM⊥CD,又AD⊥CD,AM∩AD=A, 所以CD⊥平面PAD,所以CD⊥PA, 又由(1)可知BD⊥PA,BD∩CD=D, 所以PA⊥平面ABCD. --------------10分 故VDACM=VMACD=×PA×S△ACD=××2××2×2= --------------12分 19.解:(1)设抽到相邻两个月的数据为亊件, 因为从组数据中选取组数据共有种情况, 每种情况都是等可能出现的,其中抽到相邻两个月的数据的情况有种, 所以. --------------3分 (2)由数据求得, 由公式求得, 再由,得关于的线性回归方程为.--------------8分 (3)当时,; 同样,当时,, 所以,该小组所得线性回归方程是理想的. --------------12分 20.解:(1)将曲线C的方程化为x2+y2-2ax-y=0⇒(x-a)2+(y-)2=a2+, 可知曲线C是以点(a,)为圆心,以为半径的圆. --------------3分 (2)△AOB的面积S为定值. 证明如下:在曲线C的方程中令y=0,得ax(x-2a)=0,得点A(2a,0), 在曲线C方程中令x=0,得y(ay-4)=0,得点B(0,), 所以S=|OA|·|OB|=·|2a|·||=4(定值). --------------4分 (3)直线l与曲线C方程联立得,设,则 即即解得或 当时,满足;当时,满足故或-------------12分 21. 【解析】(1),在处取到极值,即 经检验,时,在处取到极小值. (2),令, 当时,,在上单调递减,又,时,,不满足在上恒成立 当时,二次函数开口向上,对称轴为,过 ①当即时,在上恒成立,,从而在上单调递增,又时,成立,满足在上恒成立 ②当即0<时,存在>1,使时,<0,单调递减, >0,单调递增, ,又,故不满足题意 当时,二次函数开口向下,对称轴为,在单调递减,, ,在上单调递减,又,时,,故不满足题意 综上所述, (3)证明:由(1)知令,当时,(当且仅当时取“”) ∴当时, . 即当,有 .--------------12分 22.解:(1)由直线的参数方程消去参数可得, 化简并整理可得直线的一般方程为,则极坐标方程 由可得,即,所以圆的标准方程为.--------5分 (2)易知点在圆内,且在直线上,联立圆的方程和直线的参数方程方程组,设,所以,所以,则,同理, .---------10分 23. --------------------------------5分 (Ⅱ)由(Ⅰ)知,则. 因为,所以, ………………6分 则,(当且仅当时等号成立)……………7分 ,(当且仅当时等号成立)………………8分 ,(当且仅当时等号成立)………………9分 则(当且仅当时等号成立), 即,即 ---------------------10分 查看更多