高考数学专题复习:期末测试卷必修一
第三章期末测试卷 必修一
一、选择题
1、设f(x)=2x-x-4,x0是函数f(x)的一个正数零点,且x0∈(a,a+1),其中a∈N,则a=( )
A.1 B.2
C.3 D.4
2、对任意实数x>-1,f(x)是2x,log(x+1)和1-x中的最大者,则f(x)的最小值( )
A.在(0,1)内 B.等于1
C.在(1,2)内 D.等于2
3、用min{a,b,c}表示a,b,c三个数中的最小值
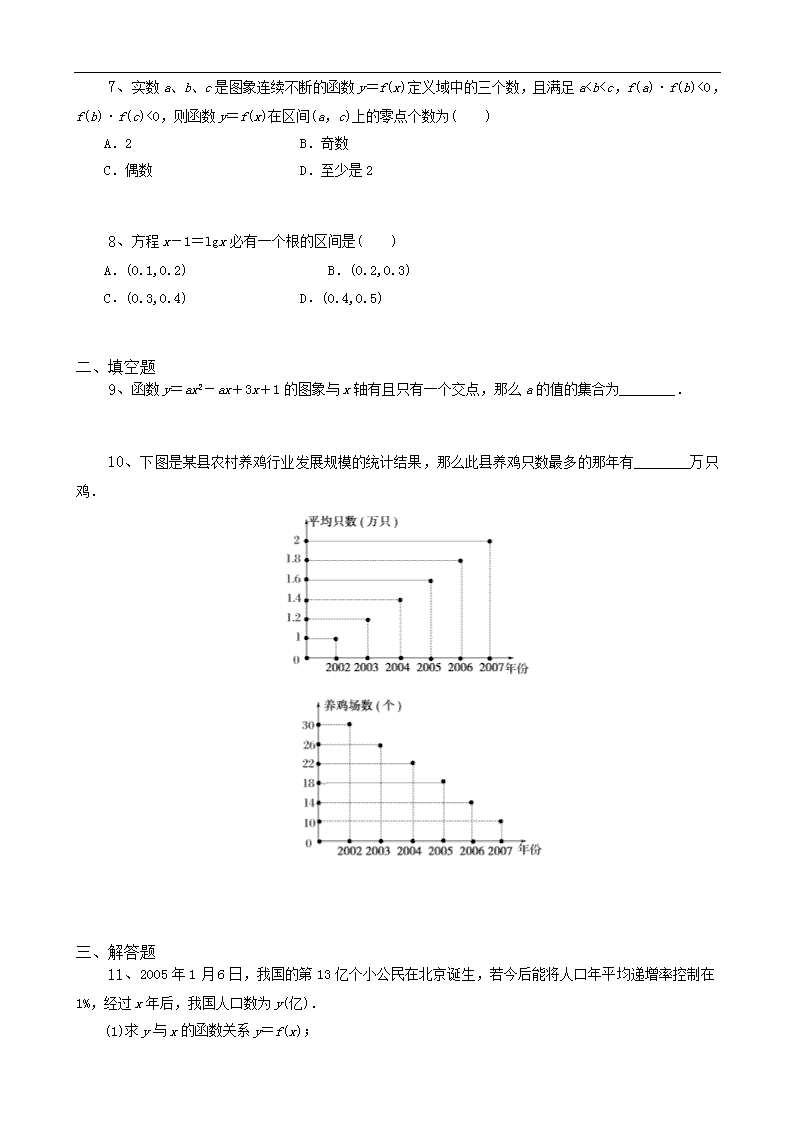
设f(x)=min{2x,x+2,10-x}(x≥0),则f(x)的最大值为( )
A.4 B.5 C.6 D.7
4、下列函数中,与函数y=有相同定义域的是( )
A.f(x)=lnx B.f(x)=
C.f(x)=|x| D.f(x)=ex
5、某企业2008年12月份的产值是这年1月份产值的p倍,则该企业2008年年度产值的月平均增长率为( )
A. B.-1
C. D.
6、已知函数f(x)=ex-x2+8x,则在下列区间中f(x)必有零点的是( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
7、实数a、b、c是图象连续不断的函数y=f(x)定义域中的三个数,且满足a
0满足,∴a=2,故选B.
2、B[解析] 在同一坐标系中,作出函数y=2x,y=log(x+1),y=1-x的图象,由条件知f(x)的图象是图中实线部分,显见f(x)的最小值在y=2x与y=1-x交点(0,1)处取得.
∴最小值为f(0)=1.
3、C
[解析] 由题意,可画下图:f(x)的最大值在A点,
由,得,∴f(x)的最大值为6.
4、A[解析] 函数y=的定义域为(0,+∞),故选A.
5、B[解析] 设1月份产值为a,增长率为x,则
ap=a(1+x)11,∴x=-1,故选B.
6、B[解析] f(-1)=-9<0,f(0)=e0=1>0,故f(x)在(-1,0)上有一实数解,故选B.
7、D[解析] 由f(a)f(b)<0 知y=f(x)在(a,b)上至少有一实根,由f(b)f(c)<0知y=f(x)在(b,c)上至少有一实根,故y=f(x)在(a,c)上至少有2实根.
8、A [解析] 设f(x)=x-1-lgx,f(0.1)=0.1>0,
f(0.2)=0.2-1-lg0.2=0.2-lg2<0
∴f(0.1)f(0.2)<0,故选A.
二、填空题
9、{0,1,9}
[解析] 当a=0时,y=3x+1的图象与x轴只有一个交点;当a≠0时,由Δ=(3-a)2-4a=0得a=1或9.
10、31.2
[解析] 2002年,30×1=30万只,
2003年,26×1.2=31.2万只,
2004年,22×1.4=30.8万只,
2005年,18×1.6=28.8万只,
2006年,14×1.8=25.2万只,
2007年,10×2=20万只.
三、解答题
11、[分析] 关键是理解年递增率的意义
2005年人口数为13(亿)
经过1年,2006年人口数为13+13×1%=13(1+1%)(亿)
经过2年,2007年人口数为13(1+1%)+13(1+1%)×1%=13(1+1%)(1+1%)=13(1+1%)2(亿).
经过3年,2008年人口数为13(1+1%)2+13(1+1%)2×1%=13(1+1%)3(亿).
[解析] (1)由题设条件知,经过x年后我国人口总数为13(1+1%)x(亿).
∴y=f(x)=13(1+1%)x.
(2)∵此问题以年作为单位时间 ,∴此函数的定义域是N*.
(3)y=13(1+1%)x是指数型函数,
∵1+1%>1,13>0,∴y=13(1+1%)x是增函数,
即只要递增率为正数时,随着时间的推移,人口的总数总在增长.
12、[解析] (1)由图象知,当x=600时,y=400;当x=700时,y=300,代入y=kx+b中,得
解得
∴y=-x+1 000(500≤x≤800).
(2)销售总价=销售单价×销售量=xy,成本总价=成本单价×销售量=500y,
代入求毛利润的公式,得
s=xy-500y=x(-x+1 000)-500(-x+1 000)
=-x2+1 500x-500 000
=-(x-750)2+62 500(500≤x≤800).
∴当销售单价为750元/件时,可获得最大毛利润62 500元,此时销售量为250件.