- 2021-06-20 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学(人教A版)必修4:2-2-1同步试题(含详解)
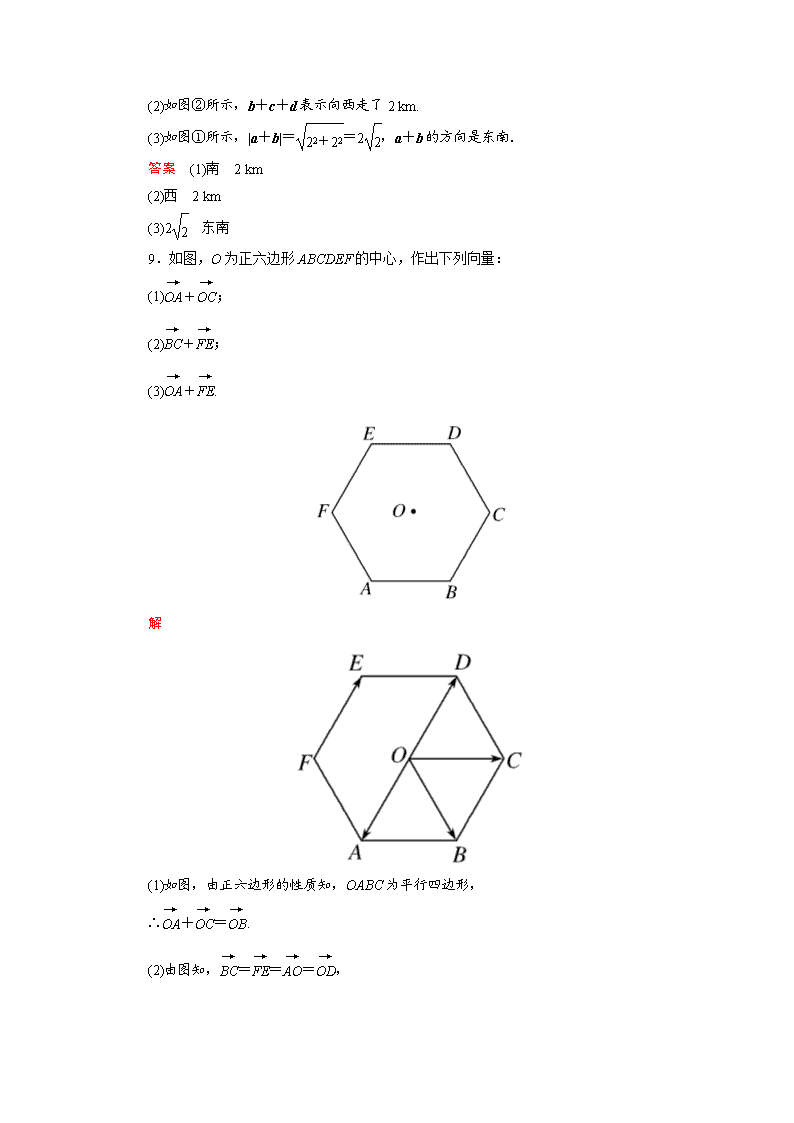
高中数学(人教A版)必修4同步试题 1.在四边形ABCD中,=+,则( ) A.ABCD一定是矩形 B.ABCD一定是菱形 C.ABCD一定是正方形 D.ABCD一定是平行四边形 解析 由向量的平行四边形法则知,ABCD一定是平行四边形. 答案 D 2.向量(+)+(+)+化简后等于( ) A. B. C. D. 解析 (+)+(+)+=(+)+(++)=+0=,故选C. 答案 C 3.向量a,b皆为非零向量,下列说法不正确的是( ) A.向量a与b反向,且|a|>|b|,则向量a+b与a的方向相同 B.向量a与b反向,且|a|<|b|,则向量a+b与a的方向相同 C.向量a与b同向,则向量a+b与a的方向相同 D.向量a与b同向,则向量a+b与b的方向相同 解析 向量a与b反向,且|a|<|b|,则a+b应与b方向相同,因此B错. 答案 B 4.对任意向量a,b,在下式中:①a+b=b+a;②(a+b)+c=b+(a+c);③|a+b|=|a|+|b|;④|a+b|≤|a|+|b|,恒成立的有( ) A.1个 B.2个 C.3个 D.4个 解析 因为向量加法满足交换律,结合律,所以①,②恒成立.|a+b|=|a|+|b|仅当a与b同向或有零向量时成立,所以③不恒成立.由向量模的几何定义知④恒成立.故选C. 答案 C 5.正方形ABCD的边长为1,=a,=c,=b,则|a+b+c|为( ) A.0 B. C.3 D.2 解析 |a+b+c|=|2c|=2|c|=2.应选D. 答案 D 6.若a,b满足|a|=2,|b|=3,则|a+b|的最大值为__________,最小值为__________. 解析 当a与b同向时,|a+b|有最大值|a|+|b|=5. 当a与b反向时,|a+b|有最小值|b|-|a|=1. 答案 5 1 7.下列结论: ①a-a=0;②a-b=a+(-b);③设a,b为任意向量,则|a+b|>0;④若∥,且||=2012,||=1,则|+|=2013. 其中正确的有________. 解析 a-a=0,故①错;②正确;③中当a+b=0时,不成立,故③错;④中当与方向相反时,不正确,故④错. 答案 ② 8.设a表示“向东走了2 km”,b表示“向南走了2 km”,c表示“向西走了2 km”,d表示“向北走了2 km”,则 (1)a+b+c表示向________走了________km; (2)b+c+d表示向________走了________km; (3)|a+b|=________,a+b的方向是________. 解析 (1)如图所示,a+b+c 表示向南走了2 km. (2)如图②所示,b+c+d表示向西走了2 km. (3)如图①所示,|a+b|==2,a+b的方向是东南. 答案 (1)南 2 km (2)西 2 km (3)2 东南 9.如图,O为正六边形ABCDEF的中心,作出下列向量: (1)+; (2)+; (3)+. 解 (1)如图,由正六边形的性质知,OABC为平行四边形, ∴+=. (2)由图知,===, ∴+=+=. (3)∵=,=, ∴+ =+=+=0. 10. 如右图所示,P,Q是△ABC的边BC上的两点,且=. 求证:+=+. 证明 由图可知=+, =+, ∴+=+++. ∵=, 又与模相等,方向相反, 故+=+=0. ∴+=+. 教师备课资源 1.在Rt△ABC中,若∠A=90°,||=2,||=3,则+的模等于( ) A. B.2 C.3 D.5 解析 由题意知|+|===,应选A. 答案 A 2.已知下列各式: ①++; ②(+)++; ③+++; ④+++. 其中结果为0的个数为( ) A.1 B.2 C.3 D.4 解析 ①++=+=0. ②(+)++=++=+=≠0. ③+++=+≠0. ④+++=++=+=0. 其中结果为0的有两个. 答案 B 3.①如果非零向量a与b的方向相同或相反,那么a+b的方向必与a,b之一的方向相同; ②△ABC中,必有++=0; ③若++=0,则A,B,C为一个三角形的三个顶点; ④若a,b均为非零向量,则|a+b|与|a|+|b|一定相等. 其中真命题的个数为( ) A.0 B.1 C.2 D.3 解析 ①不正确,当a+b=0时,不成立.②正确.③不正确.当A,B,C共线时,不成立.④不正确.因为|a+b|≤|a|+|b|.应选B. 答案 B 4.已知正方形ABCD的边长为1,则|+++|等于________. 解析 |+++|=|2|=2. 答案 2 5.如图,在正六边形ABCDEF中,=a,=b,求,,. 解 如下图,连接FC交AD于点O,连接OB,由平面几何知识得四边形ABOF和四边形ABCO均为平行四边形. 根据向量的平行四边形法则,有 =+=a+b. ∴=2=2a+2b. 在平行四边形ABCO中,=+=a+a+b=2a+b. 而===a+b, 由三角形法则得 =+=b+a+b=a+2b.查看更多