2020届高考数学一轮复习（课时训练·文）第13章 选修部分60证明不等式的基本方法

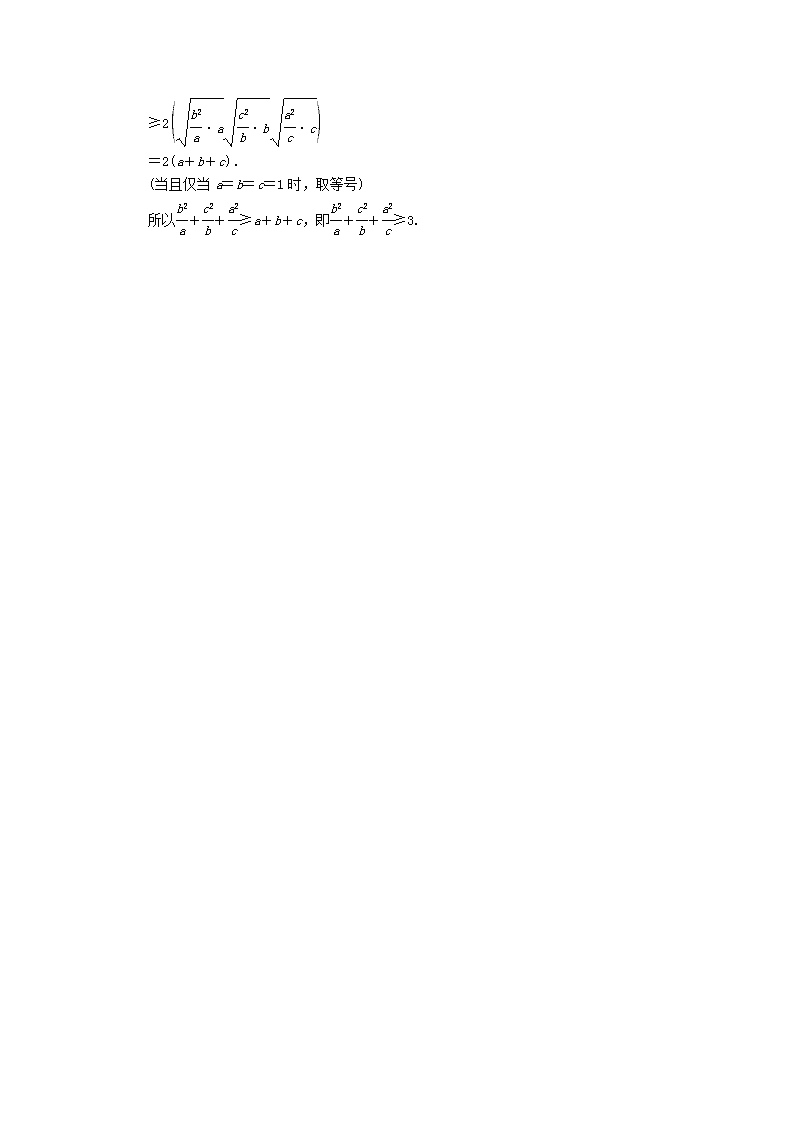
申明敬告： 本站不保证该用户上传的文档完整性，不预览、不比对内容而直接下载产生的反悔问题本站不予受理。

文档介绍

2020届高考数学一轮复习（课时训练·文）第13章 选修部分60证明不等式的基本方法

‎【课时训练】证明不等式的基本方法 解答题 ‎1．(2018广州五校联考)已知函数f(x)＝|x＋3|＋|x－1|，其最小值为t.‎ ‎(1)求t的值；‎ ‎(2)若正实数a，b满足a＋b＝t，求证：＋≥.‎ ‎(1)【解】因为|x＋3|＋|x－1|＝|x＋3|＋|1－x|≥|x＋3＋1－x|＝4，所以f(x)min＝4，即t＝4.‎ ‎(2)【证明】由(1)得a＋b＝4，故＋＝1，＋＝＝＋1＋＋≥＋2＝＋1＝，当且仅当b＝2a，即a＝，b＝时取等号，故＋≥.‎ ‎2．(2018湖北八校联考)设不等式－2<|x－1|－|x＋2|<0的解集为M，a，b∈M.　‎ ‎(1)证明：<；‎ ‎(2)比较|1－4ab|与2|a－b|的大小，并说明理由．‎ ‎(1)【证明】记f(x)＝|x－1|－|x＋2|＝ 由－2<－2x－1<0解得－0.‎ 所以|1－4ab|2>4|a－b|2，故|1－4ab|>2|a－b|.‎ ‎3．(2018广州模拟)已知定义在R上的函数f(x)＝|x－m|＋|x|，m∈N*，存在实数x使f(x)<2成立．‎ ‎(1)求实数m的值；‎ ‎(2)若α，β≥1，f(α)＋f(β)＝4，求证：＋≥3.‎ ‎【解】(1)因为|x－m|＋|x|≥|(x－m)－x|＝|m|.‎ 要使不等式|x－m|＋|x|<2有解，则|m|<2，‎ 解得－2
查看更多

相关文章

您可能关注的文档