2018-2019学年江西省会昌中学高二上学期第一次月考数学（理）试题（卓越班） Word版

2018-2019学年江西省会昌中学高二上学期第一次月考数学（理）试题（卓越班） Word版

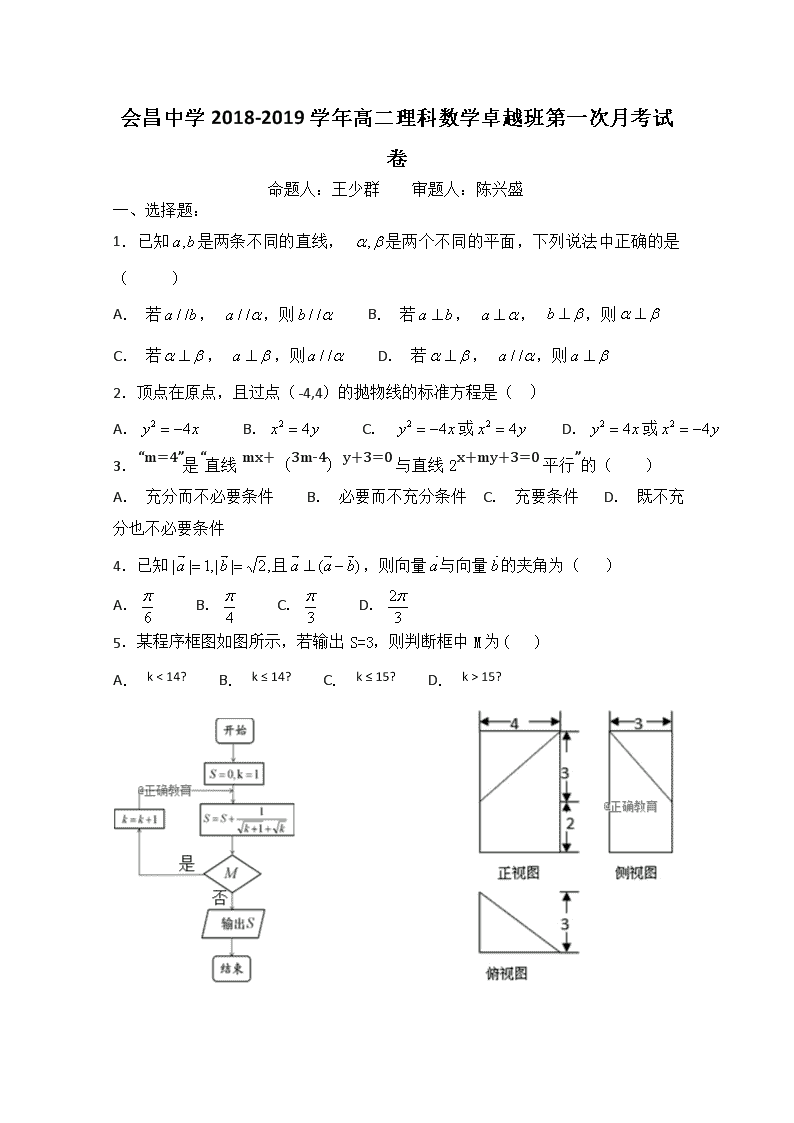
会昌中学2018-2019学年高二理科数学卓越班第一次月考试卷 命题人：王少群 审题人：陈兴盛 一、选择题：‎ ‎1．已知是两条不同的直线， 是两个不同的平面，下列说法中正确的是（ ）‎ A． 若， ，则 B． 若， ， ，则 C． 若， ，则 D． 若， ，则 ‎2．顶点在原点，且过点（-4,4）的抛物线的标准方程是（ ）‎ A． B． C． 或 D．或 ‎3．“m=4”是“直线mx+（3m-4）y+3=0与直线2x+my+3=0平行”的（　　）‎ A． 充分而不必要条件 B． 必要而不充分条件 C． 充要条件 D． 既不充分也不必要条件 ‎4．已知且，则向量与向量的夹角为（ ）‎ A． B． C． D． ‎ ‎5．某程序框图如图所示，若输出S=3，则判断框中M为( )‎ A． ‎ B． C． D． ‎ ‎ ‎ ‎(第5题图) (第9题图) (第12题图) ‎ ‎6．等差数列的前n项和为Sn，若S5=5，那么的最小值为（ ）‎ A． 4 B． 2 C． 2 D． ‎ ‎7．在△ABC中，a,b,c分别为角A,B,C所对的边，若，则△ABC是（ ）‎ A． 直角三角形 B． 等腰三角形 C． 等腰直角三角形 D． 直角三角形或等腰三角形 ‎8．已知等比数列的前n项和为，，且满足成等差数列，则等于( )‎ A． B． C． D． ‎ ‎9．若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示，则所截去的三棱锥的外接球的表面积等于( )‎ A． B． C． D． ‎ ‎10．在ABC中，内角A,B,C的对边分别为a,b,c.若ABC的面积为S，且,则ABC外接圆的面积为（ ）‎ A． B．2 C． D． ‎ ‎11．设双曲线C:的两条渐近线互相垂直，顶点到一条渐近线的距离为1，则双曲线的一个焦点到一条渐近线的距离为（ ）‎ A． 2 B． C． D． 4‎ ‎12．如图, 在正方体中,AB=1 , 过直线的平面平面 ‎,则平面截该正方体所得截面的面积为（ ）‎ A． B．2 C． D．‎ 二、填空题：‎ ‎13．为了了解高一(10)班53名同学的牙齿健康状况,需从中抽取10名同学做医学检验,现已对53名同学编号为00,01,02,…,50,51,52.从下面所给的随机数表的第1行第3列的5开始从左向右读下去,则选取的第5个号码为_________。‎ 随机数表如下:‎ ‎0154　3287　6595　4287　5346‎ ‎7953　2586　5741　3369　8324‎ ‎4597　7386　5244　3578　6241‎ ‎14．已知变量满足约束条件，若恒成立，则实数的取值范围为_____．‎ ‎15．给出下列三种说法：‎ ‎①命题p：∃x0∈R，tan x0＝1，命题q：∀x∈R，x2－x＋1>0，则命题“p∧()”是假命题．‎ ‎②已知直线l1：ax＋3y－1＝0，l2：x＋by＋1＝0，则l1⊥l2的充要条件是＝－3.‎ ‎③命题“若x2－3x＋2＝0，则x＝1”的逆否命题为“若x≠1，则x2－3x＋2≠0”．‎ 其中所有正确说法的序号为________________．‎ ‎16．已知双曲线的左、右焦点分别为点，抛物线与双曲线在第一象限内相交于点P，若，则双曲线的离心率为______．‎ 三、解答题 ‎17．设：实数满足，其中； ：实数使得方程表示双曲线.‎ ‎（1）当时，若“”为真命题，求的取值范围；（2）若是的充分不必要条件，求实数的取值范围.‎ ‎18．在中，内角A,B,C的对边分别为a,b,c，且满足.‎ ‎（1）证明：b,a,c成等差数列； （2）已知的面积为，求a的值.‎ ‎19．某社区为了解辖区住户中离退休老人每天的平均户外“活动时间”，从辖区住户的离退休老人中随机抽取了100位老人进行调查，获得了每人每天的平均户外“活动时间”（单位：小时），活动时间按照[0，0.5），[0.5，1），…，[4，4.5]从少到多分成9组，制成样本的频率分布直方图如图所示．‎ ‎（Ⅰ）求图中a的值；（Ⅱ）估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数；‎ ‎（III）在[1.5，2）、[2，2.5）这两组中采用分层抽样抽取9人，再从这9人中随机抽取2人，求抽取的两人恰好都在同一个组的概率．‎ ‎ ‎ ‎（第21题图） ‎ ‎20．已知数列的前n项和为，且满足 ‎（1）求数列的通项公式和前n项和；‎ ‎（2）设，令，求 ‎21．如图，在四棱锥P-ABCD中，底面ABCD是菱形，，PD平面ABCD，PD=AD=1，点E,F分别为AB和PD中点. ‎ ‎（1）求证：直线AF平面PEC；（2）求证：AC面PBD；‎ ‎（3）求PE与平面PDB所成角的正弦值.‎ ‎ ‎ ‎22．已知椭圆C的方程为，P在椭圆上，椭圆的左顶点为A，左、右焦点分别为，的面积是的面积的倍．‎ ‎（1）求椭圆C的方程；（2）直线与椭圆C交于M，N，连接并延长交椭圆C于D,E,连接DE，指出与之间的关系，并说明理由．‎ 会昌中学高二理科数学卓越班第一次月考试卷答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C C B B A D C A D B D ‎13、41 14、 15、①③ 16、‎ ‎17、（1）当时，由，解得, ‎ 由 ，解得. ‎ 因为“”为真， .‎ ‎∴实数的值取值范围是. ‎ ‎（2）是的充分不必要条件等价于若是的充分不必要条件， ‎ 由（1）知，条件对应的集合为： .‎ 记满足条件的实数的集合为 ‎ 由题意. ‎ 当时， ，满足；‎ 当时， ，满足；‎ 当时， ，要使，只需或，‎ 所以或. 综上实数的取值范围为： 或. ‎ ‎18、（1）由题设，‎ 即 ‎ 由三角形内角和定理有由正弦定理有 成等差数列 ‎（2）由得，根据，‎ 由余弦定理又由(1)得，代入得 ，.‎ ‎19、（I）解：由频率分布直方图，可知，辖区住户中离退休老人每天的平均户外“活动时间”在[0，0.5）的频率为0.08×0.5=0.04．‎ 同理，在[0.5，1），[1,1.5），[1.5，2）[2，2.5），[2.5，3）[3，3.5），[3.5，4），[4，4.5]的频率分别为0.08，0.15，0.5a，0.25，0.15，0.07，0.04，0.02‎ 由解得a=0.40．‎ ‎（II）解：设“活动时间”的中位数为m小时．‎ 因为前5组的频率之和为0.04+0.08+0.15+0.20+0.25=0.72＞0.5，‎ 而前4组的频率之和为0.04+0.08+0.15+0.20=0.47＜0.5，所以2≤m＜2.5．‎ 由0.50×（m2）=0.50.47，解得m=2.06．‎ 所以估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数为2.06小时．‎ ‎（III）解：由题意得平均户外活动时间在[1.5，2），[2，2.5）中的人数分别有20人、25人，按分层抽样的方法分别抽取4人、5人，记作A，B，C，D及a，b，c，d，e从9人中随机抽取2人，共有36种，分别为：‎ ‎（A，B），（A，C），（A，D），（A，a），（A，b），（A，c），（A，d），（A，e），（B，C），（B，D），（B，a），（B，b），（B，c），（B，d），（B，e），（C，D），（C，a），（C，b），（C，c），（C，d），（C，e），（D，a），（D，b），（D，c），（D，d），（D，e），（a，b），（a，c），（a，d），（a，e），（b，c），（b，d），（b，e），（c，d），（c，e），（d，e）‎ 在同一组的有：（A，B），（A，C），（A，D），（B，C），（B，D），（C，D），（a，b），（a，c），（a，d），（a，e），（b，c），（b，d），（b，e），（c，d）（c，e），（d，e）．共16种，故抽取的两人恰好都在同一个组的概率．‎ ‎20、（1）由题意可知则 即所以为公比的等比数列 令则所以，.‎ ‎（2）则 ‎.‎ ‎21、（1）证明：作交于．‎ ‎∵点为中点，∴，∵，∴，∴为平行四边形，∴，‎ ‎∵平面，平面，∴直线平面．‎ ‎（2）∵底面是菱形，∴，‎ ‎∵平面，平面，∴∵，∴平面；‎ ‎（3）连接，，∵点，分别为和中点，∴，‎ ‎∵平面，∴平面，‎ 根据直线与平面所成角的定义可得：为与平面所成角或补角，‎ 中，，，，，‎ ‎∴，∴与平面所成角的正弦值为．‎ ‎22、（1）由的面积是的面积的倍，可得，即，‎ 又，所以，‎ 由在椭圆上，可得，所以，可得，，所以椭圆的方程为． ‎ ‎（2）设，则，‎ 故直线的方程为，‎ 由消去整理得， ‎ 又，代入上式化简得，‎ 设，，则，所以，．‎ 又直线的方程为，同理可得，． ‎ 所以 ‎， ‎ 所以．‎