命题角度4-4 空间中角的问题（第01期）-2018年高考数学（文）备考之百强校大题狂练系列

命题角度4-4 空间中角的问题（第01期）-2018年高考数学（文）备考之百强校大题狂练系列

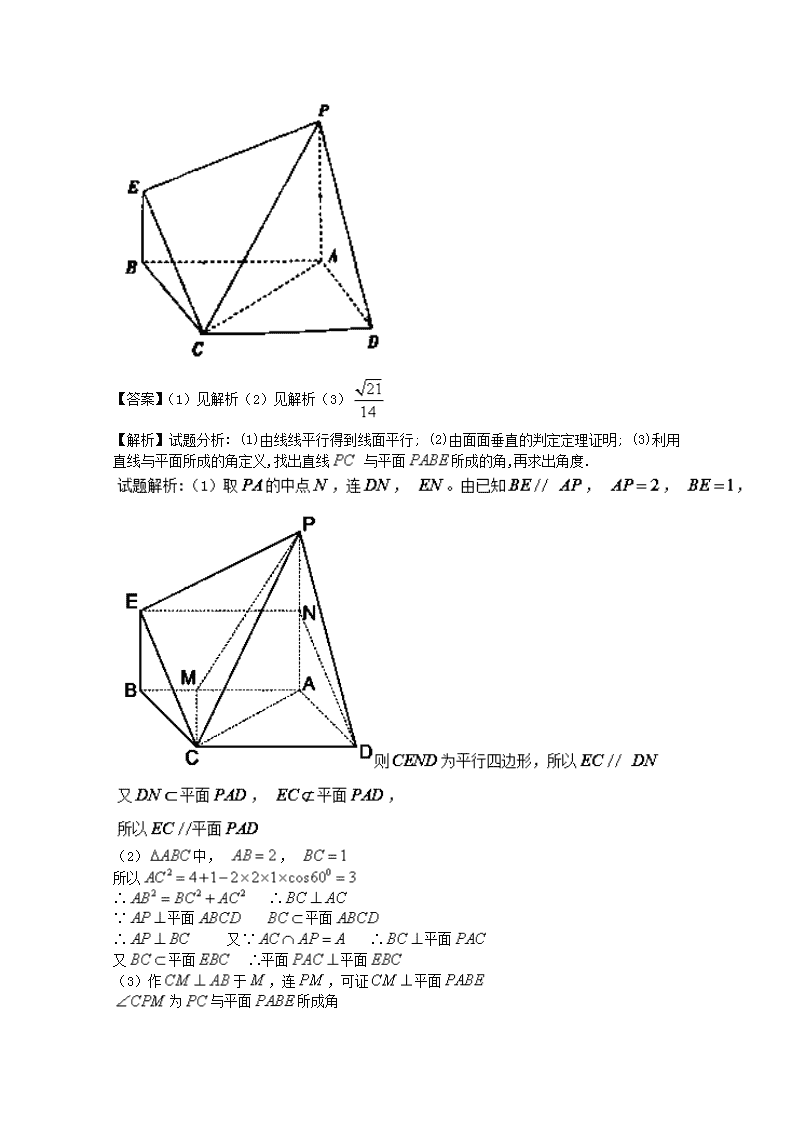
‎2018届高考数学（文）大题狂练 命题角度4：空间中角的问题 ‎1.如图，在四棱锥中， 平面， ，且， ， ， 为线段上一点， ，且为的中点.‎ ‎（Ⅰ）证明： 平面；‎ ‎（Ⅱ）求证：平面平面；‎ ‎（Ⅲ）求直线与平面所成角的正弦值.‎ ‎【答案】（1）见解析（2）‎ ‎【解析】【试题分析】（1）运用两线面平行的判定定理分析推证；（2）运用面面垂直的判定定理分析推证；（3）依据题设条件运用线面角的定义先找出线面角，再借助解三角形的知识求解：‎ ‎（1）取，中点，，连，，，由为中点，所以，且.由，，则，又，则.‎ 所以四边形为平行四边形，所以，且面，面，则面.‎ ‎（2）∵，∴，又，所以四边形为平行四边形，故.又∵面.面，∴.又，所以面，∵面，∴面面.‎ ‎（3）过作，垂足为.由（2）知面面，面面，面，∴面，连接，.‎ 则为在平面上的射影，∴为与平面所成角. 中 ‎，‎ ‎，，‎ ‎∴与平面所成角正弦值为. ‎ 点睛：立体几何是高中数学中的传统内容之一，也是高考重点考查的内容和考点。求解本题第一问时，直接运用线面平行的判定定理进行分析推证，从而使得问题获解；解答第二问时，先运用线面垂直的判定定理证明线面垂直，再运用面面垂直的判定定理分析推证进而使得问题获解；解答第三问时，先依据题设条件运用线面角的定义先找出线面角（即斜线与其射影所成角），再借助解三角形的知识求解而获解。‎ ‎2.如图， 是平行四边形， 平面， ， ， ， .‎ ‎（1）求证： 平面；‎ ‎（2）求证：平面平面；‎ ‎（3）求直线与平面所成角的正弦值.‎ ‎【答案】（1）见解析（2）见解析（3）‎ ‎【解析】试题分析: (1)由线线平行得到线面平行; (2)由面面垂直的判定定理证明; (3)利用直线与平面所成的角定义,找出直线 与平面所成的角,再求出角度.‎ ‎（2）中， ， ‎ 所以 ‎∴ ∴ ‎ ‎∵平面 平面 ‎∴ 又∵ ∴平面 ‎ 又平面 ∴平面平面 ‎ ‎（3）作于，连，可证平面 为与平面所成角 ‎ ‎， ， ， ，‎ ‎。 ‎ 答: 直线与平面所成角的正弦值为 ‎3.已知三棱柱中， ，侧面底面， 是的中点， .‎ ‎（Ⅰ）求证： 面； ‎ ‎（Ⅱ）求直线与平面所成线面角的正弦值.‎ ‎【答案】(Ⅰ)证明见解析；(Ⅱ) .‎ 试题解析：‎ ‎（Ⅰ）取中点，连接，‎ 中， ，故是等边三角形，∴，‎ 又，而与相交于，∴面，‎ 故，又，所以，‎ 又∵侧面底面于， 在底面内，∴面.‎ ‎（Ⅱ）过作平面，垂足为，连接， 即为直线与平面所成的角，‎ 由（Ⅰ）知，侧面底面，所以平面，由等边知，‎ 又∵平面，‎ ‎∴，‎ 由（Ⅰ）知面，所以，∴四边形是正方形，‎ ‎∵，∴，‎ ‎∴在中， ，‎ 所以直线与平面所成线面角的正弦值为.‎ 点睛：(1)求直线与平面所成的角的一般步骤：‎ ‎①找直线与平面所成的角，即通过找直线在平面上的射影来完成；‎ ‎②计算，要把直线与平面所成的角转化到一个三角形中求解．‎ ‎(2)作二面角的平面角可以通过垂线法进行，在一个半平面内找一点作另一个半平面的垂线，再过垂足作二面角的棱的垂线，两条垂线确定的平面和二面角的棱垂直，由此可得二面角的平面角．‎ ‎4.如图，在棱台中， 与分别是棱长为1与2的正三角形，平面平面，四边形为直角梯形， ， ， 为中点， （， ）.‎ ‎（1）设中点为， ，求证： 平面；‎ ‎（2）若到平面的距离为，求直线与平面所成角的正弦值.‎ ‎【答案】（1）见解析（2）‎ ‎【解析】试题分析：（1）延长三棱台的三条侧棱，设交点为， 时为的中点，设中点为，连梯形中，中位线，根据线面平行的判定定理可得平面；同理可证平面，然后再根据面面平行的判定定理可得，平面平面，进而可证命题成立；（2）设中点为，连，在中作且交于点，由面面垂直的性质定理，可得，又，所以平面，所以为到平面的距离， ‎ 且为直线与平面所成角；再根据面面垂直的性质定理，可得可得， 中为的中点 ，由此即可求出线面角的正弦值.‎ 又且平面， 平面 所以平面平面 所以平面 ‎（2）设中点为，连，在中作且交于点，‎ 又，所以平面，‎ 所以为到平面的距离， ‎ 且为直线与平面所成角 平面，所以， 中 为的中点 ‎ ‎ 直线与平面所成角的正弦值为.‎ ‎5.如图，在等腰梯形中， ， ， ，四边形为矩形， ，平面平面，点为线段中点．‎ ‎（Ⅰ）求异面直线与所成的角的正切值；‎ ‎（Ⅱ）求证：平面平面；‎ ‎（Ⅲ）求直线与平面所成角的正弦值．‎ ‎【答案】（1）见解析（2）‎ ‎【解析】【试题分析】（１）借助异面直线所成角的定义找出角，再运用解三角形的知识求解；（２）依据题设线面垂直＼面面垂直的判定定理推证；（３）借助线面角的定义先找出线面角，再运用解直角三角形求解：‎ ‎（Ⅰ）解：取的中点，连接， ．‎ ‎∵四边形为矩形， 为线段中点，‎ ‎∴且，‎ ‎∴，‎ ‎∴为异面直线与所成的角．‎ 在中， ， ，‎ ‎∴且，‎ 又∵平面 平面，‎ ‎∴平面，‎ ‎∴．‎ 在中， ， ．‎ ‎（Ⅲ）过点作，‎ 由第（Ⅱ）问知平面平面，‎ ‎∴平面，‎ ‎∴为直线与平面所成的角.‎ 在中， ， ，‎ ‎∴，∴，‎ ‎∴，‎ ‎∴直线与平面所成角的正弦值为.‎ ‎6.如图，在菱形中， 与相交于点， 平面， .‎ ‎（I）求证： 平面；‎ ‎（II）当直线与平面所成的角的余弦值为时，求证： ；‎ ‎（III）在（II）的条件下，求异面直线与所成的余弦值.‎ ‎【答案】（I）见解析；（II）见解析；（III）．‎ ‎【解析】试题分析：‎ ‎（I）要证与平面垂直，只要证与平面内两条相交直线垂直即可，这由已知线面垂直可得一个，又由菱形对角线垂直又得一个，由此可证；（II）由已知线面垂直得平面，从而知为直线与平面所成的角，从而可得，然后计算出三线段的长，由勾股定理逆定理可得垂直；‎ ‎（III）取中点，则有，从而可得异面直线所成的角，再解相应三角形可得．‎ 试题解析：‎ ‎（I）平面 ；‎ ‎（III）取边的中点，连接且为所求的角或其补角，而在中， 中 异面直线与所成的余弦值为.‎