2019届高三数学上学期月考试题（一）理（含解析）

2019届高三数学上学期月考试题（一）理（含解析）

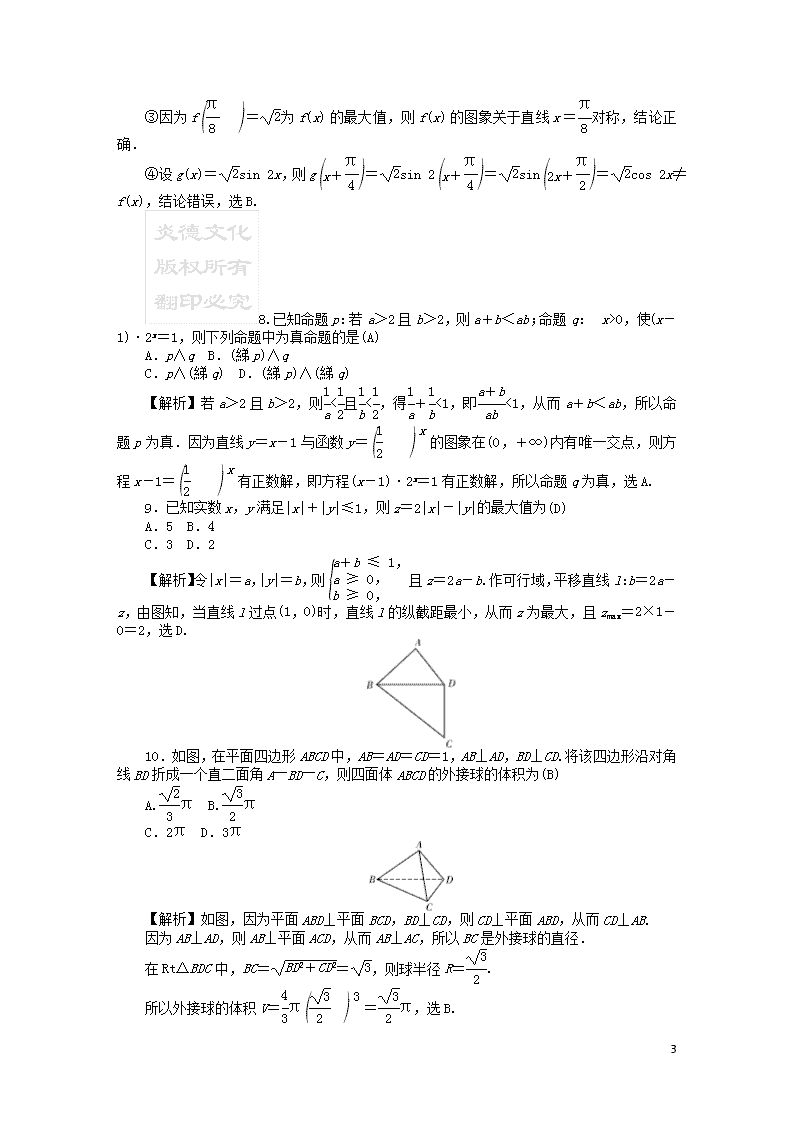
‎2019届高三数学上学期月考试题（一）理（含解析）‎ 时量：120分钟 满分：150分 一、选择题：本大题共12小题，每小题5分，共60分，在每小题的四个选项中，只有一项是符合题目要求的．‎ ‎1．设复数z＝x＋yi，其中x，y是实数，i是虚数单位，若＝x＋i，则复数z的共轭复数在复平面内对应的点位于(D)‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ A．第一象限 B．第二象限 ‎ C．第三象限 D．第四象限 ‎【解析】由已知，y＝(1－i)(x＋i)＝x＋1＋(1－x)i，则y＝x＋1，且1－x＝0，即x＝1，y＝2.‎ 所以＝x－yi＝1－2i，所对应的点(1，－2)位于第四象限，选D.‎ ‎2．已知向量a与b的夹角是，且|a|＝1，|b|＝4，若(3a＋λb)⊥a，则实数λ的值为(B)‎ A. B．－ C. D．－ ‎【解析】由已知，(3a＋λb)·a＝0，即3a2＋λb·a＝0，所以3＋2λ＝0，即λ＝－，选B.‎ ‎3．下列说法中正确的是(C)‎ A．若样本数据x1，x2，…，xn的平均数为5，则样本数据2x1＋1，2x2＋1，…，2xn＋1的平均数为10‎ B．用系统抽样法从某班按学号抽取5名同学参加某项活动，若抽取的学号为5，16，27，38，49，则该班学生人数可能为60‎ C．某种圆环形零件的外径服从正态分布N(4，0.25)(单位：cm)，质检员从某批零件中随机抽取一个，测得其外径为5.6 cm，则这批零件不合格 D．对某样本通过独立性检验，得知有95%的把握认为吸烟与患肺病有关系，则在该样本吸烟的人群中有95%的人可能患肺病 ‎【解析】对于A，若x1，x2，…，xn的平均数为5，则2x1＋1，2x2＋1，…，2xn＋1的平均数为2×5＋1＝11，所以说法错误；‎ 对于B，由抽取的号码可知样本间隔为11，则对应的人数为11×5＝55人．若该班学生人数为60，则样本间隔为60÷5＝12，所以说法错误．‎ 对于C，因为μ＝4，σ＝0.5，则(u－3σ，u＋3σ)＝(2.5，5.5)，因为5.6(2.5，5.5)，则这批零件不合格，所以说法正确．‎ 对于D，有95%的把握认为吸烟与患肺病有关系，是指对该样本所得结论：“吸烟与患肺病有关系”有95%的正确性，所以说法错误．选C.‎ ‎4．已知(n∈N*)的展开式中各项的二项式系数之和为128，则其展开式中含项的系数是(A)‎ A．－84 B．84 ‎ C．－24 D．24‎ ‎【解析】由已知，2n＝128，得n＝7，所以Tr＋1＝C(2x2)7－r＝(－1)r·27－rCx14－3r.‎ 9‎ 令14－3r＝－1，得r＝5，所以展开式中含项的系数为(－1)527－5C＝－84，选A.‎ ‎5.已知函数f(x)是定义在R上的奇函数，且f(x)在R上单调递增，若a，b，c成等差数列，且b＞0，则下列结论正确的是(A)‎ A．f(b)＞0，且f(a)＋f(c)＞0 ‎ B．f(b)＞0，且f(a)＋f(c)＜0‎ C．f(b)＜0，且f(a)＋f(c)＞0 ‎ D．f(b)＜0，且f(a)＋f(c)＜0‎ ‎【解析】由已知，f(b)＞f(0)＝0.因为a＋c＝2b＞0，则a＞－c，从而f(a)＞f(－c)＝－f(c)，‎ 即f(a)＋f(c)＞0，选A.‎ ‎6．设x为区间[－2，2]内的均匀随机数，则计算机执行下列程序后，输出的y值落在区间内的概率为(C)‎ A. B. C. D. ‎【解析】因为当x∈[－2，0]时，y＝2x∈；‎ 当x∈(0，2]时，y＝2x＋1∈(1，5]．‎ 所以当y∈时，x∈[－1，1]，其区间长度为2，所求的概率P＝＝，选C.‎ ‎7．已知函数f(x)＝sin 2x－2sin2x＋1，给出下列四个结论：(B)‎ ‎①函数f(x)的最小正周期是2π；②函数f(x)在区间上是减函数；③函数f(x)的图象关于直线x＝对称；④函数f(x)的图象可由函数y＝sin 2x的图象向左平移个单位得到．其中正确结论的个数是 A．1 B．2 ‎ C．3 D．4‎ ‎【解析】f(x)＝sin 2x＋cos 2x＝sin.‎ ‎①因为ω＝2，则f(x)的最小正周期T＝π，结论错误．‎ ‎②当x∈时，2x＋∈，则f(x)在区间上是减函数，结论正确．‎ ‎③因为f＝为f(x)的最大值，则f(x)的图象关于直线x＝对称，结论正确．‎ 9‎ ‎④设g(x)＝sin 2x，则g＝sin 2＝sin＝cos 2x≠f(x)，结论错误，选B.‎ ‎8.已知命题p：若a＞2且b＞2，则a＋b＜ab；命题q：x>0，使(x－1)·2x＝1，则下列命题中为真命题的是(A)‎ A．p∧q B．(綈p)∧q ‎ C．p∧(綈q) D．(綈p)∧(綈q)‎ ‎【解析】若a＞2且b＞2，则<且<，得＋<1，即<1，从而a＋b＜ab，所以命题p为真．因为直线y＝x－1与函数y＝的图象在(0，＋∞)内有唯一交点，则方程x－1＝有正数解，即方程(x－1)·2x＝1有正数解，所以命题q为真，选A.‎ ‎9．已知实数x，y满足|x|＋|y|≤1，则z＝2|x|－|y|的最大值为(D)‎ A．5 B．4 ‎ C．3 D．2‎ ‎【解析】令|x|＝a，|y|＝b，则且z＝2a－b.作可行域，平移直线l：b＝2a－z，由图知，当直线l过点(1，0)时，直线l的纵截距最小，从而z为最大，且zmax＝2×1－0＝2，选D.‎ ‎10．如图，在平面四边形ABCD中，AB＝AD＝CD＝1，AB⊥AD，BD⊥CD.将该四边形沿对角线BD折成一个直二面角A―BD―C，则四面体ABCD的外接球的体积为(B)‎ A.π B.π C．2π D．3π ‎【解析】如图，因为平面ABD⊥平面BCD，BD⊥CD，则CD⊥平面ABD，从而CD⊥AB.‎ 因为AB⊥AD，则AB⊥平面ACD，从而AB⊥AC，所以BC是外接球的直径．‎ 在Rt△BDC中，BC＝＝，则球半径R＝.‎ 所以外接球的体积V＝π＝π，选B.‎ ‎11．设双曲线－＝1(a>0，b>0)的左、右焦点分别为F1，F2，O为坐标原点，若双曲线上存在点M满足|MF1|＝2|MO|＝2|MF2|，则双曲线的离心率为(C)‎ 9‎ A．6 B．3 C. D. ‎【解析】过点M作x轴的垂线，垂足为A，因为|MO|＝|MF2|，则A为OF2的中点，所以|AF2|＝，|AF1|＝.设|MF2|＝m，则|MF1|＝2m.在Rt△MAF1中，|MA|2＝4m2－c2.‎ 在Rt△MAF2中，|MA|2＝m2－，则4m2－c2＝m2－，即3m2＝2c2.‎ 因为|MF1|－|MF2|＝2a，则m＝2a，所以3×(2a)2＝2c2，即c2＝6a2，所以e＝＝，选C.‎ ‎12．对于给定的正整数n，设集合Xn＝{1，2，3，…，n}，AXn，且A≠．记I(A)为集合A中的最大元素，当A取遍Xn的所有非空子集时，对应的所有I(A)的和记为S(n)，则S(2 018)＝(D)‎ A．2 018×22 018＋1 B．2 018×22 017＋1 ‎ C．2 017×22 017＋1 D．2 017×22 018＋1‎ ‎【解析】对于集合Xn，满足I(A)＝1的集合A只有1个，即{1}；满足I(A)＝2的集合A有2个，即{2}，{1，2}；满足I(A)＝3的集合A有4个，即{3}，{1，3}，{2，3}，{1，2，3}；…；‎ 满足I(A)＝n的集合A有2n－1个，所以S(n)＝1＋2·2＋3·22＋…＋n·2n－1.‎ 由错位相减法，得S(n)＝(n－1)2n＋1，所以S(2 018)＝2 017×22 018＋1，选D.‎ 二、填空题，本大题共4小题，每小题5分，共20分．‎ ‎13．已知cos＝，则sin＝__－__．‎ ‎【解析】sin＝sin＝cos 2＝2cos2－1＝－.‎ ‎14．如图，在△ABC中，＝，P是线段BD上一点，若＝m＋，则实数m的值为____．‎ ‎【解析】因为＝，则＝4，所以＝m＋.‎ 因为B，P，D三点共线，则m＋＝1，所以m＝.‎ ‎15．已知函数f(x)＝|2x－1|－a，若存在实数x1，x2(x1≠x2)，使得f(x1)＝f(x2)＝－1，则a的取值范围是__(1，2)__．‎ ‎【解析】令f(x)＝－1，则|2x－1|＝a－1.据题意，直线y＝a－1与函数y＝|2x－1|的图象两个不同的交点，由图可知，0＜a－1＜1，即1＜a＜2.‎ ‎16．设数列{an}的前n项和为Sn，已知a1＝1，且Sn＝4－an(n∈N*)，则数列{an}的通项公式是an＝____．‎ ‎【解析】当n≥2时，an＝Sn－Sn－1＝an－1－an，则an＝an－1，‎ 9‎ 即＝，所以数列{}是首项为1，公比为的等比数列，则＝，即an＝.‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答．‎ ‎(一)必考题：60分．‎ ‎17．(本小题满分12分)‎ 如图，在平面四边形ABCD中，AB＝4，AD＝2，∠BAD＝60°，∠BCD＝120°.‎ ‎(1)若BC＝2，求∠CBD的大小；‎ ‎(2)设△BCD的面积为S，求S的取值范围．‎ ‎【解析】(1)在△ABD中，因为AB＝4，AD＝2，∠BAD＝60°，则 BD2＝AB2＋AD2－2AB·AD·cos∠BAD＝16＋4－2×4×2×＝12，所以BD＝2.(3分)‎ 在△BCD中，因为∠BCD＝120°，BC＝2，BD＝2，由＝，得 sin∠CDB＝＝＝，则∠CDB＝45°.(5分)‎ 所以∠CBD＝60°－∠CDB＝15°.(6分)‎ ‎(2)设∠CBD＝θ，则∠CDB＝60°－θ.‎ 在△BCD中，因为＝＝4，则BC＝4sin(60°－θ)．(8分)‎ 所以S＝BD·BC·sin∠CBD＝4sin(60°－θ)sin θ＝4sin θ ‎＝3sin 2θ－2sin2θ＝3sin 2θ－(1－cos 2θ)＝3sin 2θ＋cos 2θ－ ‎＝2sin(2θ＋30°)－.(11分)‎ 因为0°＜θ＜60°，则30°＜2θ＋30°＜150°，b>0)的一个焦点与抛物线y2＝4x的焦点重合，且直线y＝x与圆x2＋y2－10x＋20＝0相切．‎ ‎ (1)求椭圆C的方程；‎ ‎(2)设斜率为k且不过原点的直线l与椭圆C相交于A、B两点，O为坐标原点，直线OA，OB的斜率分别为k1，k2，若k1，k，k2成等比数列，推断|OA|2＋|OB|2是否为定值？若是，求出此定值；若不是，说明理由．‎ ‎【解析】(1)因为抛物线y2＝4x的焦点为(，0)，则c＝，所以a2－b2＝3.(2分)‎ 因为直线bx－ay＝0与圆(x－5)2＋y2＝5相切，则＝，即a2＝4b2.(4分)‎ 解得a2＝4，b2＝1，所以椭圆C的方程是＋y2＝1.(5分)‎ ‎(2)设直线l的方程为y＝kx＋m(m≠0)，点A(x1，y1)，B(x2，y2)，‎ 将直线l的方程代入椭圆方程，得x2＋4(kx＋m)2＝4，即(4k2＋1)x2＋8kmx＋4m2－4＝0，‎ 则x1＋x2＝－，x1x2＝.(7分)‎ 由已知，k2＝k1k2＝＝，则k2x1x2＝(kx1＋m)(kx2＋m)，‎ 即km(x1＋x2)＋m2＝0，所以－＋m2＝0，即(1－4k2)m2＝0.‎ 因为m≠0，则k2＝，即k＝±，从而x1＋x2＝2m，x1x2＝2m2－2.(10分)‎ 所以|OA|2＋|OB|2＝x＋y＋x＋y＝x＋(kx1＋m)2＋x＋(kx2＋m)2‎ ‎＝(k2＋1)(x＋x)＋2km(x1＋x2)＋2m2＝(k2＋1)[(x1＋x2)2－2x1x2]＋2km(x1＋x2)＋2m2.‎ ‎＝[4m2－2(2m2－2)]－2m2＋2m2＝5为定值．(12分)‎ ‎21．(本小题满分12分)‎ 已知函数f(x)＝ex－a(x－1)，a∈R，e为自然对数的底数．‎ ‎(1)若存在x0∈(1，＋∞)，使f(x0)＜0，求实数a的取值范围；‎ ‎(2)若f(x)有两个不同零点x1，x2，证明：x1＋x2＞x1x2.‎ ‎【解析】(1)解法一：f′(x)＝ex－a.(1分)‎ 9‎ ‎①若a≤0，因为ex>0，则f′(x)>0，此时f(x)在R上单调递增．‎ 当x∈(1，＋∞)时，f(x)＞f(1)＝e＞0，不合题意．(2分)‎ ‎②若a＞0，由f′(x)>0，得ex>a，即x＞ln a，则f(x)在(ln a，＋∞)上单调递增，在(－∞，ln a)上单调递减，所以f(x)min＝f(ln a)＝eln a－a(ln a－1)＝a(2－ln a)．(4分)‎ 据题意，则ln a＞2，即a>e2，所以a的取值范围是(e2，＋∞)．(5分)‎ 解法二：当x∈(1，＋∞)时，由f(x)＜0，得ex.(1分)‎ 设g(x)＝(x>1)，据题意，当x∈(1，＋∞)时，a＞g(x)能成立，则a>g(x)min.(2分)‎ 因为g′(x)＝＝(x>1)，(3分)‎ 则当x＞2时，g′(x)>0，g(x)单调递增；当1＜x＜2时，g′(x)<0，g(x)单调递减．(4分)‎ 所以g(x)min＝g(2)＝e2，故a的取值范围是(e2，＋∞)．(5分)‎ ‎(2)由题设，f(x1)＝f(x2)＝0，即则ex1·ex2＝a2(x1－1)(x2－1)，‎ 即ex1＋x2＝a2(x1x2－x1－x2＋1)．(7分)‎ 要证x1＋x2＞x1x2，只要证ex1＋x2e2，且x1＜ln a＜x2，从而2ln a－x2＜ln a.‎ 因为f(x)在(－∞，ln a)上单调递减，所以只要证f(x1)>f(2ln a－x2)，即证f(x2)>f(2ln a－x2)．(9分)‎ 设h(x)＝f(x)－f(2ln a－x)，则 h′(x)＝f′(x)＋f′(2ln a－x)＝ex－2a＋e2ln a－x＝ex＋－2a≥2－2a＝0，‎ 所以h(x)在R上单调递增．因为x2＞ln a，则h(x2)>h(ln a)＝f(ln a)－f(ln a)＝0，‎ 即f(x2)－f(2ln a－x2)>0，即f(x2)>f(2ln a－x2)，所以原不等式成立．(12分)‎ ‎(二)选考题：共10分．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题计分．‎ ‎22．(本小题满分10分)选修4－4：坐标系与参数方程 在平面直角坐标系xOy中，以坐标原点O为极点，x轴正半轴为极轴，建立极坐标系，已知曲线C1的极坐标方程为ρ＝4cos θ，直线l的参数方程为(t为参数)．‎ ‎(1)求曲线C1的直角坐标方程及直线l的普通方程；‎ ‎(2)若曲线C2的参数方程为(α为参数)，点P在曲线C1上，其极角为，点Q为曲线C2上的动点，求线段PQ的中点M到直线l的距离的最大值．‎ ‎【解析】(1)由ρ＝4cos θ，得ρ2＝4ρcos θ.将ρ2＝x2＋y2，x＝ρcos θ代入，得 曲线C1的直角坐标方程为x2＋y2－4x＝0.(3分)‎ 由得x＋2y＝3，所以直线l的普通方程为x＋2y－3＝0.(5分)‎ ‎(2)由题设，点P的极坐标为，其直角坐标为(2，2)．(7分)‎ 9‎ 设点Q(2cos α，sin α)，则PQ的中点M的坐标为.(8分)‎ 点M到直线l的距离d＝＝≤.‎ 所以点M到直线l的距离的最大值为.(10分)‎ ‎23．(本小题满分10分)选修4－5：不等式选讲 已知函数f(x)＝|x＋a|＋|x－2|，其中a为实常数．‎ ‎ (1)若函数f(x)的最小值为3，求a的值；‎ ‎(2)若当x∈[1，2]时，不等式f(x)≤|x－4|恒成立，求a的取值范围．‎ ‎【解析】(1)因为f(x)＝|x＋a|＋|x－2|≥|(x＋a)－(x－2)|＝|a＋2|，(3分)‎ 当且仅当(x＋a)(x－2)≤0时取等号，则f(x)min＝|a＋2|.‎ 令|a＋2|＝3，则a＝1或a＝－5.(5分)‎ ‎(2)当x∈[1，2]时，f(x)＝|x＋a|＋2－x，|x－4|＝4－x.‎ 由f(x)≤|x－4|，得|x＋a|＋2－x≤4－x，即|x＋a|≤2，即―2≤x＋a≤2，即―x－2≤a≤－x＋2.‎ 所以(－x－2)max≤a≤(－x＋2)min.(8分)‎ 因为函数y＝－x－2和y＝－x＋2在[1，2]上都是减函数，则当x＝1时，(－x－2)max＝－3；‎ 当x＝2时，(－x＋2)min＝0，所以a的取值范围是[－3，0]．(10分)‎ 9‎