2019-2020学年河北省保定市高二上学期第四次月考数学（文）试题 word版

2019-2020学年河北省保定市高二上学期第四次月考数学（文）试题 word版

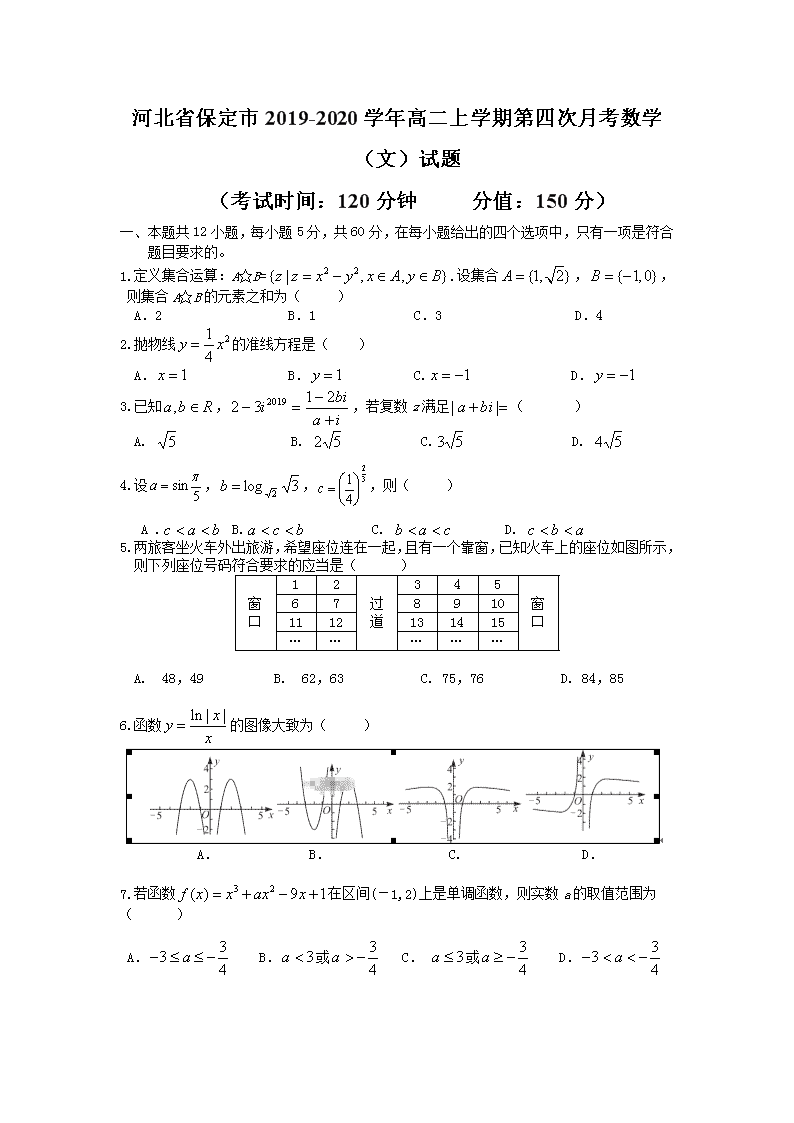
河北省保定市2019-2020学年高二上学期第四次月考数学（文）试题 ‎（考试时间：120分钟 分值：150分）‎ 一、 本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.定义集合运算：A☆B=.设集合，，则集合A☆B的元素之和为（ ）‎ A．2 B．1 C．3 D．4‎ ‎2.抛物线的准线方程是（ ） ‎ A． B． C. D．‎ ‎3.已知，，若复数z满足（ ）‎ A. B. C. D. ‎ ‎4.设，，，则（ ）‎ ‎ A . B. C. D. ‎ ‎5.两旅客坐火车外出旅游，希望座位连在一起，且有一个靠窗，已知火车上的座位如图所示，则下列座位号码符合要求的应当是（ ）‎ 窗 口 ‎1‎ ‎2‎ 过 道 ‎3‎ ‎4‎ ‎5‎ 窗 口 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ A. 48，49　　　　　B. 62，63 C. 75，76 D. 84，85‎ ‎6.函数的图像大致为（ ）‎ A． B． C. D． ‎ ‎7.若函数在区间(－1,2)上是单调函数，则实数a的取值范围为（ ）‎ A． B．或 C． 或 D．‎ ‎8.已知函数，则“”是“曲线存在垂直于直线的切线”的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎9.下列函数中，既是奇函数又具有零点的是（ ） ‎ A． B．‎ C． D．‎ ‎10.定义在R上的函数满足，当时，，则（ ）‎ A． B． C．2 D．‎ ‎11.曲线作线性变换后得到的回归方程为，则函数的单调递增区间为（ ）‎ A．(0,+∞) B．(1,+∞) C． D．‎ ‎12.点P在双曲线的右支上，其左、右焦点分别为F1，F2，直线PF1与以坐标原点O为圆心，a为半径的圆相切于点A，线段PF1的垂直平分线恰好过点F2，则双曲线的离心率为（ ）‎ A． B． C.2 D．‎ 二、填空题（每空5分，共20分）。‎ ‎13.计算___________.‎ ‎14.函数的单调递减区间为_____________.‎ ‎15.函数的图象与直线相切，则实数a的值为____________.‎ ‎16.斜率为1的直线与椭圆相交与A，B两点，则的最大值为__________.‎ 三、解答题：（共70分）解答应写出文字说明，证明过程或演算步骤。‎ ‎17.已知p:函数的定义域是R，q:方程表示焦点在x轴上的双曲线.‎ ‎（1）若p是真命题，求实数m的取值范围；‎ ‎（2）若“”是真命题，求实数m的取值范围.‎ ‎18.在直角坐标系xOy中，将圆O：经过伸缩变换 后得到曲线C，‎ 直线l的参数方程为（t为参数）.‎ ‎(1)求曲线C和直线l的普通方程；‎ ‎(2)若点P，A分别是曲线C、直线l上的任意点，求|PA|的最小值.‎ ‎19.为了巩固全国文明城市创建成果，今年某市开展了拆除违章搭建铁皮棚专项整治行为.为了了解市民对此项工作的“支持”与“反对”态度，随机从存在违章搭建的户主中抽取了男性、女性共100名进行调查，调查结果如下：‎ 支持 反对 合计 男性 ‎35‎ ‎15‎ ‎50‎ 女性 ‎30‎ ‎20‎ ‎50‎ 合计 ‎65‎ ‎35‎ ‎100‎ ‎（1）根据以上数据，判断是否有90%的把握认为对此项工作的“支持”与“反对”态度与“性别”有关；‎ ‎（2）现从参与调查的女户主中按分层抽样的方法抽取5人进行调查，分别求出所抽取的5人中持“支持”和“反对”态度的人数；‎ ‎（3）现从（2）中所抽取的5人中，再随机抽取3人赠送小礼品，求恰好抽到2人持“支持”态度的概率？‎ 参考公式：，其中.‎ 参考数据：‎ ‎0.10‎ ‎0.05‎ ‎0.01‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎20.已知函数.‎ ‎（1）求不等式的解集；‎ ‎（2）当时，恒成立，求实数的取值范围.‎ ‎21.已知椭圆与直线都经过点．直线与平行，且与椭圆C交于A，B两点，直线MA，MB与轴分别交于E，F两点．‎ ‎（1）求椭圆C的方程；‎ ‎（2）证明：△MEF为等腰三角形．‎ ‎22.已知函数．‎ ‎（1）若在处的切线与直线垂直，求实数a的值；‎ ‎（2）若对任意,都有恒成立，求实数a的取值范围.‎ 数学文答案 一、 CDBAD DABBC DD 二、 ‎13.1 14. (1,+∞) 15.2 16. ‎ 三、17.解：（1）∵函数的定义域是，‎ ‎∴.对恒成立. …………1分 ‎∴，解得：，……………4分 ‎∴是真命题时，实数的取值范围是.……………5分 ‎（2）由（1）知为真时，∴:或，…………6分 ‎∵方程表示焦点在轴上的双曲线，‎ ‎∴，解得到，∴，…………8分 ‎∵“”是真命题，‎ ‎∴，解得.……………9分 ‎∴是真命题时，实数的取值范围是.……………10分 ‎18.解：(1)由 得代入 得曲线方程为： ……………………3分 直线的普通方程为：…………………5分 ‎ ‎（2）设曲线C上任意取一点（），‎ 则到的距离为：‎ ‎，（其中）……8分 所以，当时，取得最小值为.…………10分 ‎19.解：（1），.………………3分 ‎∴没有90%的把握认为对此项工作的“支持”与“反对”态度与性别有关. .……4分 ‎（2）抽取的5名女户主中，持 “支持”态度的有人，.……………6分 持反对态度的有人. .……………8分 ‎（3）..…………12分 ‎20.解:（1）当时，，∴，故；‎ 当时，，∴，故；‎ 当时，，∴，故；‎ 综上可知：的解集为┄┄┄6分 ‎（2）当时，恒成立，∴………………8分 当时，恒成立，∴，…………10分 当时，恒成立，∴，……………11分 综上，实数的取值范围为。…………12分 21. 解：（1）由直线过点M得，…………1分 椭圆点M得…………3分 椭圆的方程为．.……………4分 ‎ ‎（2）设直线为：‎ 联立: ，得， ‎ 于是． .………………6分 设直线的斜率为，要证为等腰三角形，只需证，‎ ‎.…………………………7分 ‎，.………………9分 ‎.………………11分 所以为等腰三角形 ．.…………12分 ‎22.解：（1）解： ………………1分 ‎， ，，，由条件得， ………………4分 ‎ （2） 令，则,. …………6分 令，则当时，，单调递增，.…………7分 ①当时， 在上单调递增，；‎ 所以，当时，对任意恒成立；…………9分 ‎②当时，，，所以，存在，使（此处用“当时，存在，使”证明，扣1分），并且，当时，在上单调递减，所以，当时，，‎ 所以，当时，对任意不恒成立；…………11分 综上，的取值范围为.…………12分