2018-2019学年河北省邢台市第二中学高二上学期第二次月考数学（文）试题 Word版

2018-2019学年河北省邢台市第二中学高二上学期第二次月考数学（文）试题 Word版

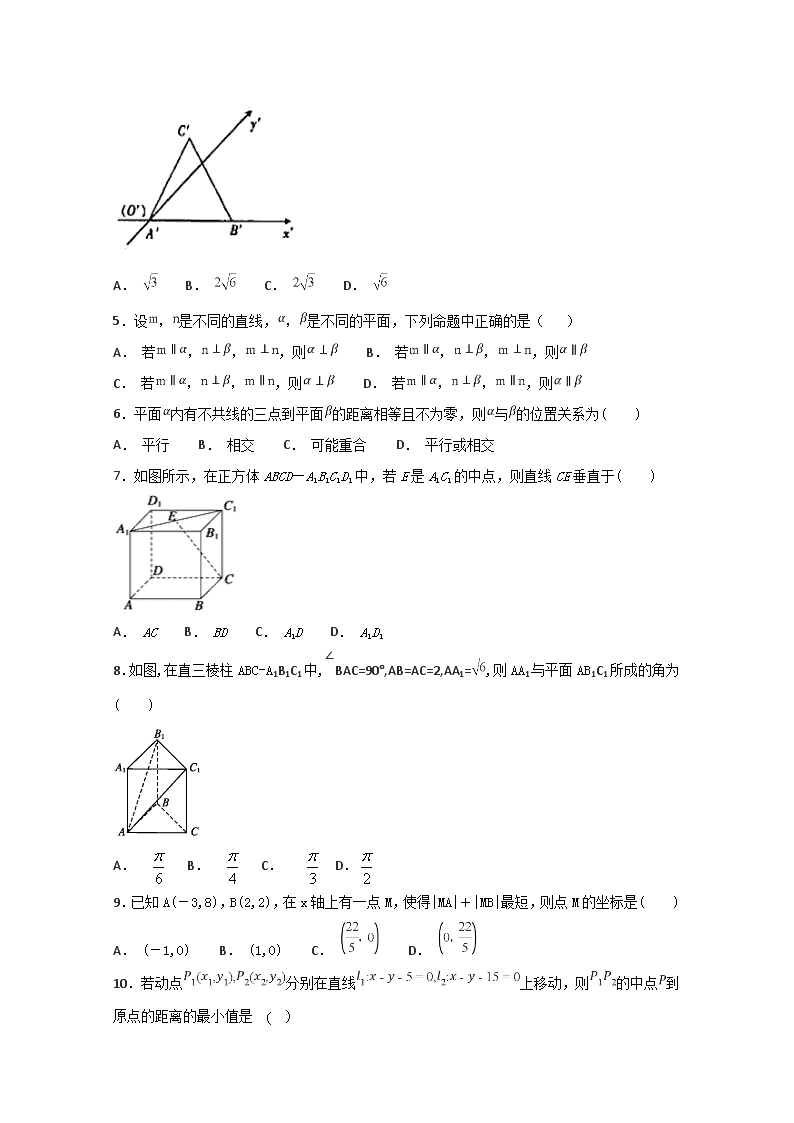
绝密★启用前 ‎2018-2019学年河北省邢台市第二中学高二上学期第二次月考数学（文）试题 考试时间：120分钟； ‎ ‎ ‎ 第I卷（选择题）‎ 一、单选题 ‎1．圆锥的轴截面是边长为的正三角形，则圆锥的表面积为（ ）‎ A． B． C． D． ‎ ‎2．某几何体的三视图如图所示，则该几何体的体积为（ ）‎ A． 2 B． C． 4 D． ‎ ‎3．将数字，，，，，书写在每一个骰子的六个表面上，做成枚一样的骰子，分别取三枚同样的这种骰子叠放成如图和所示的两个柱体，则柱体和的表面（不含地面）数字之和分别是（ ）‎ A． ， B． ， C． ， D． ，‎ ‎4．如图，已知用斜二测画法画出的三角形ABC的直观图三角形是边长为2的正三角形，则原三角形的面积为（ ）‎ A． B． C． D． ‎ ‎5．设，是不同的直线，，是不同的平面，下列命题中正确的是（ ）‎ A． 若，，，则 B． 若，，，则 C． 若，，，则 D． 若，，，则 ‎6．平面内有不共线的三点到平面的距离相等且不为零，则与的位置关系为(　　)‎ A． 平行 B． 相交 C． 可能重合 D． 平行或相交 ‎7．如图所示，在正方体ABCD—A1B1C1D1中，若E是A1C1的中点，则直线CE垂直于(　　)‎ A． AC B． BD C． A1D D． A1D1‎ ‎8．如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=,则AA1与平面AB1C1所成的角为(　　)‎ A． B． C． D． ‎ ‎9．已知A(－3,8)，B(2,2)，在x轴上有一点M，使得|MA|＋|MB|最短，则点M的坐标是(　　)‎ A． (－1,0) B． (1,0) C． D． ‎ ‎10．若动点分别在直线上移动，则的中点到原点的距离的最小值是 (　）‎ A． B． C． D． ‎ ‎11．圆x2＋(y＋1)2＝3绕直线kx－y－1＝0旋转一周所得的几何体的表面积为(　　)‎ A． 36π B． 12π C． D． 4π ‎12．一束光线从点A(－1,1)出发经x轴反射到圆C：x2＋y2－4x－6y＋12＝0上的最短路程是(　　)‎ A． 4 B． 5 C． 3 －1 D． 2‎ II卷（非选择题）‎ 二、填空题 ‎13．已知点P（1，3）为圆x2+y2+x﹣6y+m=0外一点，则实数m的取值范围为_____．‎ ‎14．已知一个正四棱锥的底面正方形边长为2，侧棱长为2，则该棱锥的侧棱与底面所成角的大小为________.‎ ‎15．若直线与直线关于直线对称，则直线恒过定点________．‎ ‎16．已知圆的圆心在直线上，且经过，两点，则圆的标准方程是__________．‎ 三、解答题 ‎17．如图所示，如果一个几何体的正视图与侧视图是全等的长方形，且边长分别是4与2，俯视图是一个边长为4的正方形 ‎（Ⅰ）求该几何体的表面积；‎ ‎（Ⅱ）求该几何体的外接球的体积 ‎18．如图，在四棱锥中，四边形为正方形， 平面， ， 是上一点.‎ ‎（1）若，求证： 平面；‎ ‎（2）若为的中点，且，求三棱锥的体积.‎ ‎19．已知直线l1：，l2：.‎ 求当m为何值时，l1，l2 (1) 平行；(2) 相交；(3) 垂直.‎ ‎20．已知圆C：x2+y2-4x-14y+45=0及点Q(-2,3).‎ ‎(1)若点P(m,m+1)在圆C上，求直线PQ的斜率.‎ ‎(2)若M是圆C上任一点，求|MQ|的取值范围.‎ ‎21．正方体ABCD-A1B1C1D1中，E为AB中点，F为CD1中点．‎ ‎（1）求证：EF∥平面ADD1A1；‎ ‎（2）求直线EF和平面CDD1C1所成角的正弦值．‎ ‎22．已知直线l：‎ ‎（1）证明直线l经过定点并求此点的坐标；‎ ‎（2）若直线l不经过第四象限，求k的取值范围；‎ ‎（3）若直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设的面积为S，求S的最小值及此时直线l的方程.‎ 参考答案[]‎ 一、1．C 2．D 3．A 4．B 5．C 6．D ‎ ‎7．B 8．A 9．B 10．A 11．B 12．A 二、13． 14．. 15． 16．‎ ‎17．（1）64.‎ ‎（2）.‎ ‎18．（1）证明见解析；（2）.‎ ‎（1）易证得和，从而得证；‎ ‎（2）由即可得解.‎ 试题解析：‎ ‎（1）证明：连接，由平面， 平面得，[‎ 又， ，‎ ‎∴平面，得，‎ 又， ，‎ ‎∴平面.‎ ‎（2）解：由为的中点得 ‎ .‎ ‎19．(1) m = – 1 (2) m≠– 1且m≠3（3）‎ ‎20．（1）；（2）≤|MQ|≤；‎ ‎ (1)根据点P在圆上求出m的值，再求直线PQ的斜率.(2)利用数形结合求|MQ|的取值范围. (1)∵P在圆C上，‎ ‎∴m2+(m+1)2-4m-14(m+1)+45=0,‎ ‎∴m=4,即P(4,5).∴kPQ=.‎ ‎(2)∵圆心C(2，7)，半径r=，|CQ|=,‎ ‎∴≤|MQ|≤.‎ ‎21．（1）见解析；（2）‎ ‎【解析】试题分析：（1）取DD1中点M，连接MA，MF，易得AEFM是平行四边形，有EF∥AM，从而得证；‎ ‎（2）因为EF∥AM，AD⊥平面CDD1C1，所以∠AMD与直线EF和平面CDD1C1所成角相等，在Rt△AMD中求解即可.‎ 试题解析：‎ ‎（1）证明：取DD1中点M，连接MA，MF，有，‎ 所以AEFM是平行四边形，‎ 所以EF∥AM，又AM⊂平面ADD1A1，EF⊄平面ADD1A1，‎ 所以EF∥平面ADD1A1，得证．‎ ‎（2）因为EF∥AM，AD⊥平面CDD1C1，所以∠AMD与直线EF和平面CDD1C1所成角相等，‎ 又在Rt△AMD中，有，所以直线EF和平面CDD1C1所成角的正弦值为．‎ ‎22.解:（1）直线l的方程可化为y=k（x+2）+1，‎ 故无论k取何值，直线l总过定点（﹣2，1）．‎ ‎（2）直线l的方程可化为y=kx+2k+1，则直线l在y轴上的截距为2k+1，‎ 要使直线l不经过第四象限，则，‎ 解得k的取值范围是k≥0．‎ ‎（3）依题意，直线l: y=kx+2k+1，在x轴上的截距为﹣，在y轴上的截距为1+2k，‎ ‎∴A（﹣，0），B（0，1+2k），‎ 又﹣＜0且1+2k＞0，‎ ‎∴k＞0，故S=|OA||OB|=×（1+2k）‎ ‎=（4k++4）≥（4+4）=4，‎ 当且仅当4k=，即k=或-时，取等号，当k=-时直线过原点，不存在三角形，故舍掉.‎ 此时直线方程为：‎