数学文卷·2018届山东省实验中学高三上学期第二次诊断考试（2017

数学文卷·2018届山东省实验中学高三上学期第二次诊断考试（2017

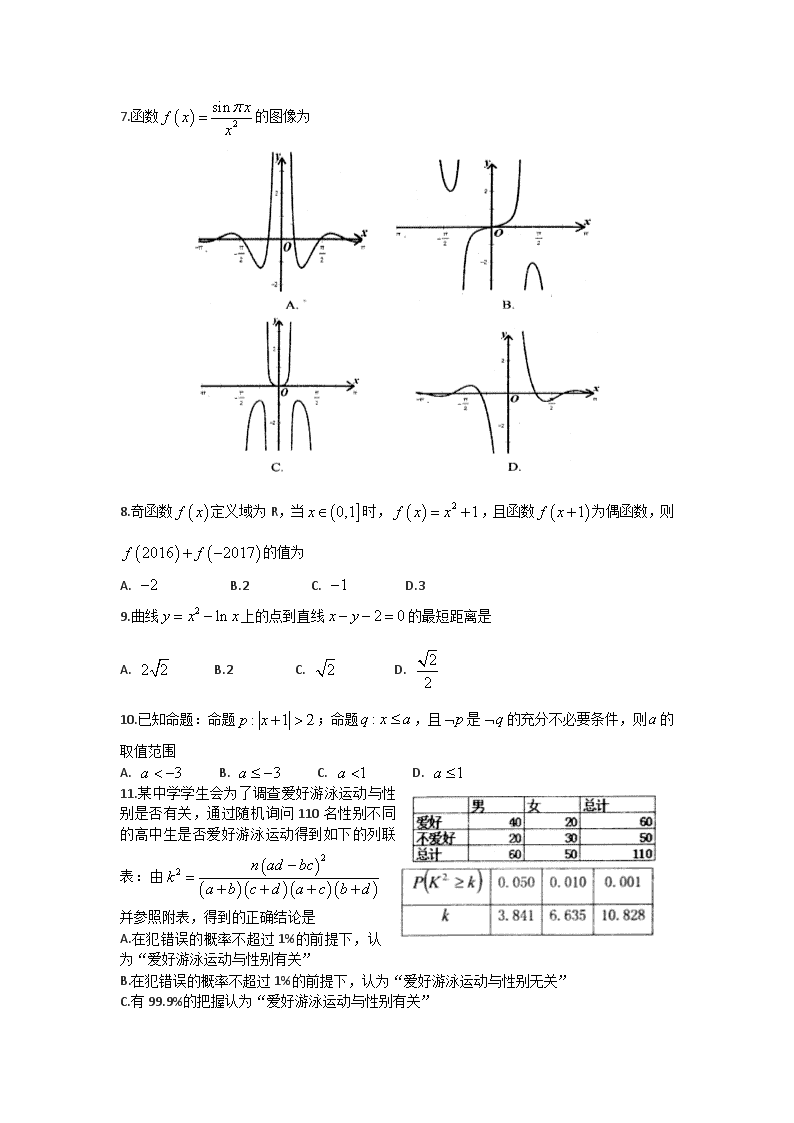
山东省实验中学2015级高三第二次诊断性考试 数学试题（文科）‎ ‎2017.11‎ 说明：本试卷满分150分，分为第I卷（选择题）和第II卷（非选择题）两部分，第I卷为第1页至第3页，第II卷为第3页至第6页.试题答案请用2B铅笔或0.5mm签字笔填涂到答题卡规定位置上，书写在试题上的答案无效考试时间120分钟.‎ 第I卷（共60分）‎ 一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.已知全集为R，集合A=,B=,则AB=‎ A. B. C. D. ‎ ‎2.命题“”的否定是 A. B. ‎ C. D. ‎ ‎3.已知函数，则的值为 A. B. C. D.4‎ ‎4.空气质量指数（Air Quality Index，简称AQI）是定量描述空气质量状况的无量纲指数，空气质量按照AQI大小分为六级：0~50为优， 51~100为良。101~150为轻度污染，151~200为中度污染，201~250为重度污染，251~300为严重污染。一环保人士记录去年某地某月10天的AQI的茎叶图。利用该样本估计该地本月空气质量状况优良（AQI≤100）的天数（这个月按30计算）‎ A.15 B‎.18 C.20 D.24‎ ‎5.若，则等于 A.2 B‎.0 C. －2 D.－4‎ ‎6.已知函数，则是 A.奇函数，且在上单调递增 B. 偶函数，且在上单调递增 C.奇函数，且在上单调递增 D. 偶函数，且在上单调递增 ‎7.函数的图像为 ‎[]‎ ‎8.奇函数定义域为R，当时，，且函数为偶函数，则的值为 A. B‎.2 C. D.3‎ ‎9.曲线上的点到直线的最短距离是 A. B‎.2 C. D. ‎ ‎10.已知命题：命题；命题，且是的充分不必要条件，则的取值范围 A. B. C. D. ‎ ‎11.某中学学生会为了调查爱好游泳运动与性别是否有关，通过随机询问110名性别不同的高中生是否爱好游泳运动得到如下的列联表：由并参照附表，得到的正确结论是 A.在犯错误的概率不超过1%的前提下，认为“爱好游泳运动与性别有关”‎ B.在犯错误的概率不超过1%的前提下，认为“爱好游泳运动与性别无关”‎ C.有99.9%的把握认为“爱好游泳运动与性别有关”‎ D.有99.9%的把握认为“爱好游泳运动与性别无关”‎ ‎12.已知是定义在上的函数，是它的导函数，且恒有成立，则 A. B. ‎ C. D. ‎ 第II卷（非选择题，共90分）‎ 二、填空题（本题共4小题，每小题5分，共20分）‎ ‎13.函数的定义域是_______________‎ ‎14.已知偶函数满足，且当时，，则=___________‎ ‎15.若函数，函数的零点个数是___________.‎ ‎16.对于函数，若存在常数，使得取定义域内的每一个值，都有，则称为准奇函数，给出下列函数 ‎①，②，③，④，⑤，⑥，其中所有准奇函数的序号是_________________。‎ 三、解答题（共70分.解答应写出文字说明、证明过程或演算步骤.第17-21为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.）‎ ‎（一）必考题：60分.‎ ‎17.根据《中华人民共和国道路交通安全法》规定：“车辆驾驶员血液酒精溶度（单位mg/100ml）/在，属于酒后驾驶；血液浓度不低于80，属于醉酒驾驶。”2017年“中秋节”晚9点开始，济南市交警队在杆石桥交通岗前设点，对过往的车辆进行检查，经过4个小时，共查处喝过酒的驾驶者60名，下图是用酒精测试仪对这60名驾驶者血液中酒精溶度进行检测后所得结果画出的频率分布直方图。‎ ‎（1）求这60名驾驶者中属于醉酒驾车的人数（图中每组包括左端点，不包括右端点）‎ ‎（2）若以各小组的中值为该组的估计值，频率为概率的估计值，求这60名驾驶者血液的酒精浓度的平均值。‎ ‎18.已知函数在与时都取得极值；‎ ‎（1）求的值与函数的单调区间；‎ ‎（2）若对，不等式恒成立，求的取值范围 ‎19.某企业为了对新研发的一批产品进行合理定价，将产品按事先拟定的价格进行试销，得到一组销售数据，如表所示：‎ 已知 ‎（1）求的值 ‎（2）已知变量具有线性相关性，求产品销量关于试销单价的线性回归方程 可供选择的数据 ‎（3）用表示（2）中所求的线性回归方程得到的与对应的产品销量的估计值。当销售数据对应的残差的绝对值时，则将销售数据称为一个“好数据”。试求这6组销售数据中的 “好数据”。‎ 参考数据：线性回归方程中的最小二乘估计分别是 ‎20.已知函数.‎ ‎（1）若曲线在点处的切线的倾斜角为，求实数的值；‎ ‎（2）若函数在区间上单调递增，求实数的范围 ‎21.已知函数，‎ ‎(I)讨论函数的单调性；‎ ‎(II)对于任意，有，求实数的范围 ‎(二)选考题：共10分.请考生在第22、23题中任选一题作答，则按所做的第一题计分.‎ ‎22.[选修4-4，坐标系与参数方程] (10分)‎ 在平面直角坐标系中，曲线C的参数方程为，以坐标原点为极点，以轴正半轴为极轴建立极坐标系，直线的极坐标方程为。‎ ‎（1）求直线的直角坐标方程和曲线C的普通方程。‎ ‎（2）设点P为曲线C上的任意一点，求点P到直线的距离的最大值。‎ ‎23.[选修4—5：不等式选讲] (10分)‎ 设函数 ‎（1）解不等式 ‎（2）对任意的实数，若求证：‎ 山东省实验中学2015级高三第二次诊断性考试 文科数学参考答案 （2017．11）‎ 一、选择题[]‎ CABBD BDACA AD 二、填空题 ‎13. 14. 1 15. 4 16. ②④⑤⑥‎ 三、解答题 ‎17．(1)由频率分布直方图可知：‎ 醉酒驾驶的频率为…………………………3分 所以醉酒驾驶的人数为(人)……………………6分 ‎（2）由频率分布直方图可知 酒精浓度 ‎25‎ ‎35‎ ‎45‎ ‎55‎ ‎65‎ ‎75‎ ‎85‎ 频率 ‎0.25‎ ‎0.15‎ ‎0.2‎ ‎0.15‎ ‎0.1‎ ‎0. 1‎ ‎0.05‎ ‎………………………9分 所以 =47 …………12分 ‎18. 解：（1）f（x）＝x3＋ax2＋bx＋c，f¢（x）＝3x2＋2ax＋b-------------------1‎ 由f¢（）＝，f¢（1）＝3＋2a＋b＝0得---------------2‎ a＝，b＝－2----------------------4‎ f¢（x）＝3x2－x－2＝（3x＋2）（x－1），函数f（x）的单调区间如下表：‎ x ‎（－¥，－）‎ ‎－‎ ‎（－，1）‎ ‎1‎ ‎（1，＋¥）‎ f¢（x）‎ ‎＋‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ f（x）‎ 极大值 ¯ 极小值 所以函数f（x）的递增区间是（－¥，－）与（1，＋¥）‎ 递减区间是（－，1）-----------------------------8‎ ‎（2）f（x）＝x3－x2－2x＋c，xÎ〔－1，2〕，当x＝－时，f（x）＝＋c 为极大值，而f（2）＝2＋c，则f（2）＝2＋c为最大值。-------------------9‎ 要使f（x）f（2）＝2＋c---------------10‎ 解得c<－1或c>2----------------------12分 ‎19.（1）‎ 又， ……………………3分 ‎（2），……………………4分 ‎……………………6分 ‎……………………7分 ‎……………………8分 ‎（3）‎ ‎，所以是好数据；‎ ‎，所以不是好数据 ‎，所以是好数据 ‎，所以不是好数据 所以是好数据 所以不是好数据 所以好数据为……………………12分 ‎20. 解：（1）‎ ‎ 则可得：.-----------------------------------5分[]‎ ‎（2）由函数在区间上单调递增 ‎ 则对一切的恒成立.-------6分 ‎ 即恒成立， ‎ ‎ 令-------9分 ‎ 函数在上单调递减，当时，‎ ‎ 所以的取值范围是.-------12分 ‎21. （1）==‎ ‎，------------------------------1‎ ① 当时，在（0，上单调递增，在（1，a-1）上单调递减；在（上递增；‎ ② 当时，在（0，上单调递增；‎ ③ 当在（0，a-1）上单调递增，在（a-1，1）上单调递减；在（上单调递增；‎ ④ 当时，在（0,1）上单调递减，在（上单调递增。----------------------------5[]‎ 综上所述：的单调性为 当时，在（0，上单调递增，在（1，a-1）上单调递减；在（上递增；‎ 当时，在（0，上单调递增；‎ 当在（0，a-1）上单调递增，在（a-1，1）上单调递减；在（上单调递增；‎ 当时，在（0,1）上单调递减，在（上单调递增。------------------6‎ ‎（Ⅲ），‎ 令 对于任意，有恒成立等价于函数 在（0，上是增函数。-------------------8‎ ‎=，令 当时，要使在（0，恒成立，因为。故只需 ， 即，即，无解-------------------------10[.‎ 当时，要使在（0，恒成立，因为，只需 即+，化简得。‎ 解得 综上所述：实数a的取值范围是。----------12‎ ‎22．解：⑴因为直线的极坐标方程为，‎ 所以，即…………………………………3分 曲线的参数方程为（为参数）‎ 所以……………………………………………………………………………5分 ‎⑵设，则到直线的距离为 ‎…………………………………………………………6分 ‎ …………………………………………………………8分 所以当时，取最大值……………………………………10分 ‎23．⑴①当时，原不等式可化为，可得，所以 当时，原不等式可化为，恒成立，所以 当时，原不等式可化为，可得，所以 综上，不等式的解集为（结果为不等式的扣1分）……………………5分 ‎（2）证明：‎ ‎…………………………………………………………10分