- 2021-06-19 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
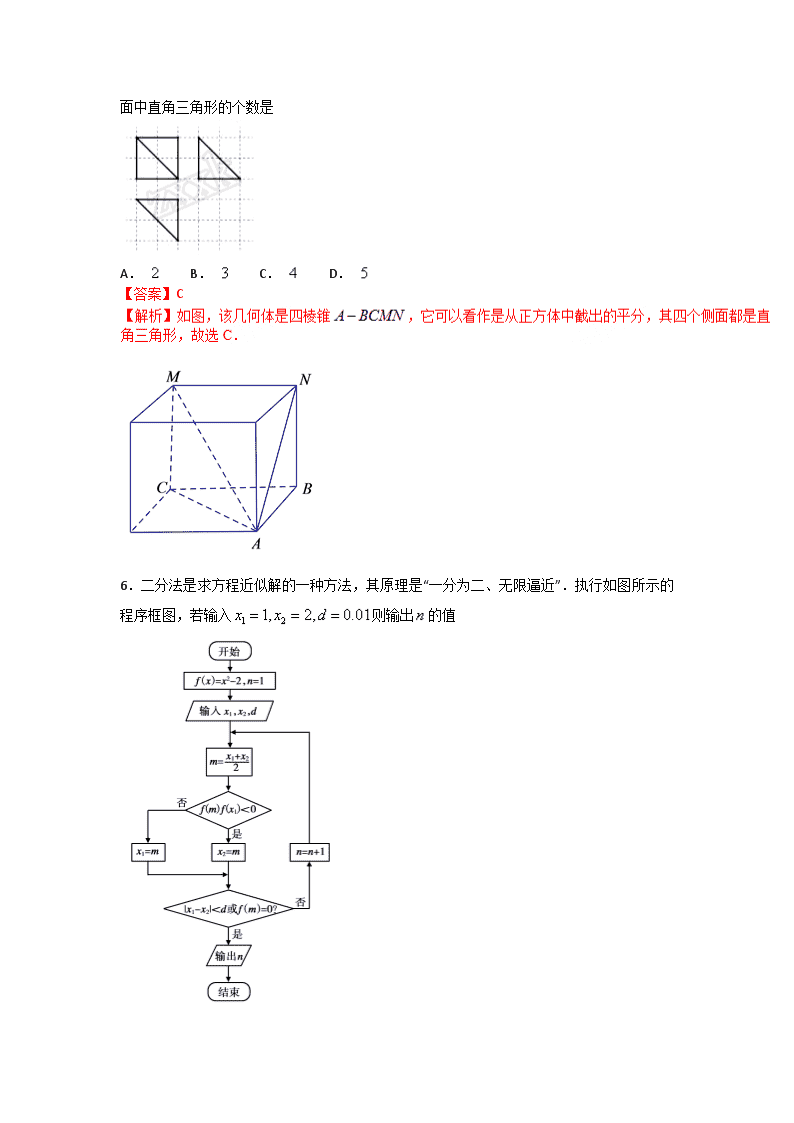
专题23 综合训练2(第02期)-2018年高考数学(理)备考之百强校小题精练系列
2018届高考数学(理)小题精练 专题23 综合训练2 1.设全集,函数的定义域为,则为( ) A. B. C. D. 【答案】A 【解析】, ,所以,故选A. 2.复数的共轭复数为,若为纯虚数,则( ) A. B. C. D. 【答案】D 3.若, , ,则大小关系为( ) A. B. C. D. 【答案】D 【解析】,即,同理,而,因此.,故选D. 4.展开式中的常数项为( ) A. 120 B. 160 C. 200 D. 240 【答案】B 【解析】 展开式的通项为 ,令 ,得,所以展开式的常数项为,选B.全品教学网 5.如图,网格纸上小正方形的边长为 ,粗线画出的是某几何体的三视图,则此几何体各面中直角三角形的个数是 A. B. C. D. 【答案】C 6.二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入则输出的值 A. B. C. D. 【答案】B 7.将函数的图象向左平移个单位,所得图象对应的函数为奇函数,则的最小值为( ) A. B. C. D. 【答案】D 【解析】 ,平移后函数 为奇函数,所以 ,解得,所以当 时, 有最小值 . 8.某学校有2500名学生,其中高一1000人,高二900人,高三600人,为了了解学生的身体健康状况,采用分层抽样的方法,若从本校学生中抽取100人,从高一和高三抽取样本数分别为,且直线与以为圆心的圆交于两点,且,则圆的方程为( ) A. B. C. D. 【答案】C 【解析】按照分层抽样的特点,高一高二高三抽取的人数分别为.所以,直线方程为 ,即,圆心 到直线的距离 ,由于 ,所以圆的半径 ,故圆的方程为 ,选C. 9.已知函数,其图象与直线相邻两个交点的距离为,若对恒成立,则的取值范围是 A. B. C. D. 【答案】D 考点:三角函数的性质 【方法点击】本题考察了三角函数的性质和图像,一般求,可根据周期求解,求可根据“五点法”求解,求值域或是单调区间时,根据复合函数求解,一般可写成,,选择将代入求的范围,(1)如果求值域,那么就根据的范围,求的范围,(2)如果求函数的单调区间,让落在相应的函数的单调区间内,(3)本题恒成立,解得,那么的范围是不等式解集的子集. 10.已知椭圆的左、右焦点分别为过作一条直线(不与轴垂直)与椭圆交于两点,如果恰好为等腰直角三角形,该直线的斜率为 A. B. C. D. 【答案】C 【解析】 设,则, ,于是,又,所以,所以, ,因此, ,直线斜率为,由对称性,还有一条直线斜率为,故选C.全品教学网 11.的展开式中, 的系数为__________. 【答案】-40 12.已知函数,若,则__________. 【答案】-6 【解析】, ,所以, . 点睛:本题函数的奇偶性,解题本质是利用奇函数的性质,因此关键是构造出一个奇函数,设,则为奇函数, ,于是有,所以, .查看更多