专题53 圆锥曲线中必考的双曲线问题-备战2018年高考高三数学一轮热点难点一网打尽
考纲要求:
1.了解双曲线的定义、几何图形和标准方程,知道其简单的几何性质(范围、对称性、顶点、离心率、渐近线). 2.了解双曲线的实际背景及双曲线的简单应用. 3.理解数形结合的思想.
基础知识回顾:
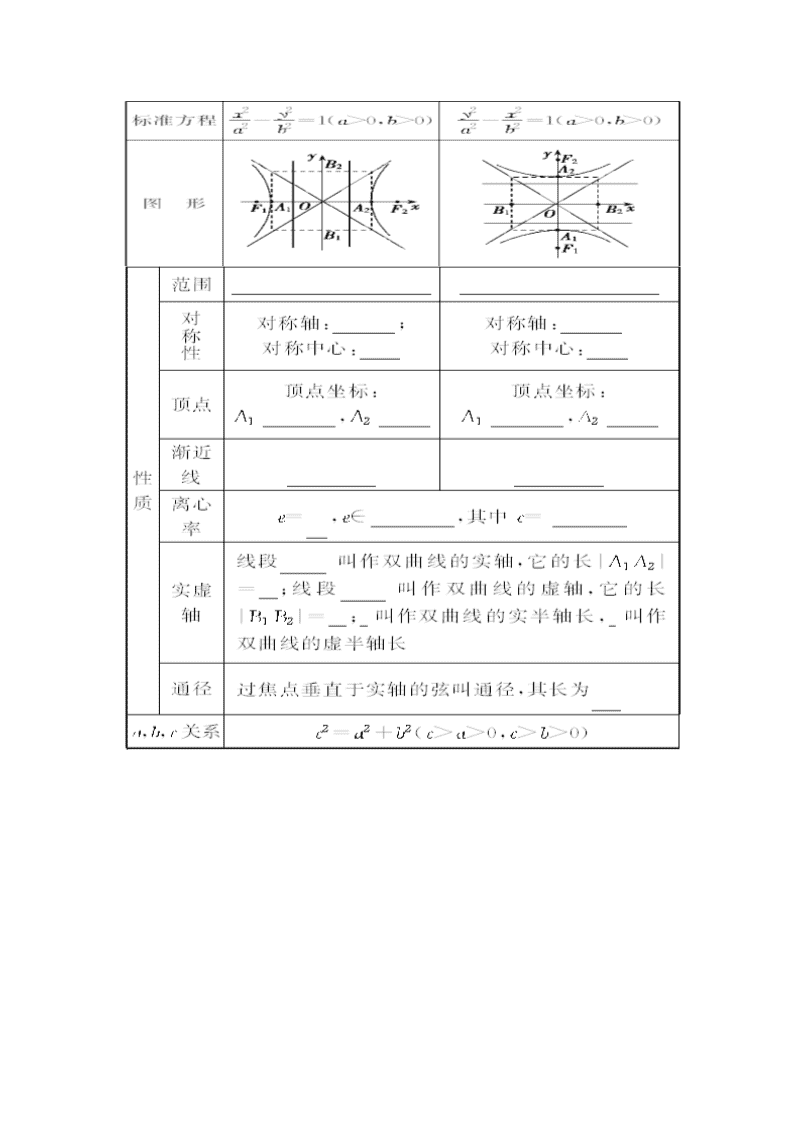
一、双曲线的标准方程和几何性质
或 或 坐标轴 坐标轴 原点 原点
二、 双曲线的定义:
平面内到两定点F1,F2的距离之差的绝对值等于常数(大于零且小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫双曲线的焦点,两焦点间的距离叫焦距.
集合P={M|||MF1|-|MF2||=2a,|F1F2|=2c,其中a、c为常数且a>0,c>0}.
(1)当a
c时,P点不存在.
应用举例:
类型一、利用定义解决焦点三角形问题
【例1】过双曲线x2-y2=8的左焦点F1有一条弦PQ在左支上,若|PQ|=7,F2是双曲线的右焦点,则△PF2Q的周长是( )
A.28 B.14-8 C.14+8 D.8
解析:由双曲线定义知,|PF2|-|PF1|=4,|QF2|-|QF1|=4,∴|PF2|+|QF2|-(|PF1|+|QF1|)=8.
又|PF1|+|QF1|=|PQ|=7,∴|PF2|+|QF2|=7+8.∴△PF2Q的周长为14+8.
【例2】【2018届广西河池市高级中学高三上第三次月考】双曲线的左、右焦点分别为,过作倾斜角为的直线与轴和双曲线右支分别交于两点,若点平分,则该双曲线的离心率是( )
A. B. C. 2 D.
【答案】A
【例3】【2018届重庆市巴蜀中学高三9月】已知双曲线C:x2169-y225=1的左、右焦点分别为F1 , F2,点M , N为异于F1 , F2的两点,且M , N的中点在双曲线C的左支上,点M关于F1和F2的对称点分别为A , B,则NA-NB的值为( )
A. 26 B. -26 C. 52 D. -52
【答案】D
点评: 在双曲线的几何性质中,应充分利用双曲线的渐近线方程,简化解题过程.同时要熟练掌握以下三方面内容:(1)已知双曲线方程,求它的渐近线;(2)求已知渐近线的双曲线的方程;(3)渐近线的斜率与离心率的关系,如k=== =.
类型二、求渐近线方程
1、利用离心率求渐近线方程
【例4】已知a>b>0,椭圆C1的方程为+=1,双曲线C2的方程为-=1,C1与C2的离心率之积为
,则C2的渐近线方程为( )
A.x±y=0 B.x±y=0 C.x±2y=0 D.2x±y=0
解析:由题意,知椭圆C1的离心率e1=,双曲线C2的离心率为e2=.
因为e1·e2=,所以=,即=,整理可得a=b.
又双曲线C2的渐近线方程为bx±ay=0,所以bx±by=0,即x±y=0.
2、利用几何性质求渐近线方程
【例5】【2018届陕西省榆林市第二中学高三上学期期中】已知双曲线x2a2-y2b2=1a>0,b>0的两个焦点分别为F1-3,0,F23,0,点P是双曲线上一点,且PF1-PF2=2,则该双曲线的渐近线方程为( )
A. y=±2x B. y=±3x C. y=±22x D. y=±23x
【答案】C
3、利用双曲线方程求渐近线方程
【例6】【2018届南宁市高三毕业班摸底联考】双曲线x225-y220=1的渐近线方程为( )
A. y=±45x B. y=±54x C. y=±15x D. y=±255x
【答案】D
【解析】由题意可得a=5,b=25,所以渐近线方程为y=±255x,选D.
点评:求曲线-=1(a>0,b>0)的渐近线的方法是令-=0,即得两渐近线方程±=0.
类型三、求离心率的值或范围.
1、利用离心率定义求离心率
【例7】【2017课标3,理10】已知椭圆C:,(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线相切,则C的离心率为( )
A. B. C. D.
【答案】A
【解析】
2、利用渐近线方程求离心率
【例8】【2017届云南省红河州高三毕业生复习统一检测】已知分别是双曲线的左、右焦点,过点且垂直于实轴的直线与双曲线的两条渐近线分别相交于两点,若坐标原点恰为的垂心(三角形三条高的交点),则双曲线的离心率为( )
A. B. C. D.
【答案】C
【解析】,则双曲线的渐近线为
则当时,
设
∵若坐标原点恰为△ABF2的垂心,
∴OA⊥BF2,即,
即,则,即,
∵ ∴,则
则离心率,故选:C.
点评:求双曲线离心率或离心率范围的两种方法:一种是直接建立e的关系式求e或e的范围;另一种是建立a,b,c的齐次关系式,将b用a,e表示,令两边同除以a或a2化为e的关系式,进而求解.
类型四、求双曲线的方程
1. 利用双曲线的定义求其方程
【例9】已知定点A(0,7)、B(0,-7)、C(12,2),以C为一个焦点作过A、B的椭圆,求另一焦点F的轨迹方程.
解析:设F(x,y)为轨迹上的任意一点,∵A、B两点在以C、F为焦点的椭圆上,
∴|FA|+|CA|=2a,|FB|+|CB|=2a(其中a表示椭圆的长半轴长),∴|FA|+|CA|=|FB|+|CB|,
∴|FA|-|FB|=|CB|-|CA|=-=2,∴|FA|-|FB|=2<14.
由双曲线的定义知,F点在以A、B为焦点,2为实轴长的双曲线的下支上,
∴点F的轨迹方程是y2-=1(y≤-1).
2、 利用渐近线方程求双曲线方程
【例10】【北省重点高中联考协作体高三上学期期中】已知双曲线()的一条渐近线过点,且双曲线的一个焦点在抛物线的准线上,则双曲线的方程为__________.
【答案】.
∴双曲线的方程为.
故答案为: .
点评:1.求双曲线方程时一是标准形式判断;二是注意a,b,c的关系易错易混.
2.双曲线的定义理解到位是解题的关键.应注意定义中的条件“差的绝对值”,弄清所求轨迹是双曲线的两支,还是双曲线的一支.若是一支,是哪一支,以确保解答的正确性.
方法、规律归纳:
1.求双曲线离心率的值
(1)直接求出,求解:已知标准方程或a,c易求时,可利用离心率公式e=求解;
(2)变用公式,整体求:如利用e===,e==;
2.双曲线的离心率与渐近线方程之间有着密切的联系,二者之间可以互求.已知渐近线方程时,可得的值,于是e2===1+2,因此可求出离心率e的值;而已知离心率的值,也可求出渐近线的方程,即=.但要注意,当双曲线的焦点所在的坐标轴不确定时,上述两类问题都有两个解.
实战演练:
1.【2017届宁夏银川市第二中学高三下学期模拟】已知双曲线()的离心率为,则的值为( )
A. B. C. D.
【答案】B
2.【2017天津,理5】已知双曲线的左焦点为,离心率为.若经过和两点的直线平行于双曲线的一条渐近线,则双曲线的方程为
(A) (B)(C)(D)
【答案】
3.【2018届安徽省屯溪第一中学高三第二次月考】设点P是双曲线x2a2-y2b2=1 (a>0,b>0)上的一点,F1,F2分别是双曲线的左、右焦点,已知∠F1PF2=900,且PF1=2PF2,则双曲线的离心率为( )
A. 2 B. 3 C. 2 D. 5
【答案】D
4.【2018届黑龙江省海林市朝鲜中学高考综合卷一】已知双曲线,若存在过右焦点的直线与双曲线交于, 两点,且,则双曲线离心率的最小值为( )
A. B. C. D.
【答案】C
【解析】因为过右焦点的直线与双曲线C相交于A、B两点,且,故直线与双曲线相交只能交于左右两只,即A 在左支,B在右支,设 , ,右焦点,因为,所以 , ,由于,所以 ,故,即 即 ,选C.
5.【2017课标II,理9】若双曲线(,)的一条渐近线被圆所截得的弦长为2,则的离心率为( )
A.2 B. C. D.
【答案】A
6.【2017课标3,理5】已知双曲线C: (a>0,b>0)的一条渐近线方程为,且与椭圆有公共焦点,则C的方程为( )
A. B. C. D.
【答案】B
【解析】双曲线C: (a>0,b>0)的渐近线方程为 ,
椭圆中: ,椭圆,即双曲线的焦点为 ,
据此可得双曲线中的方程组: ,解得: ,
则双曲线 的方程为 .
故选B.
7.【2018届湖南省衡阳市第八中学高三上学期第三次月考】已知双曲线与双曲线有相同的渐近线,则两条双曲线的四个焦点为顶点构成的四边形面积为( )
A. 10 B. 20 C. D. 40
【答案】B
8.【2018届四川省成都市第七中学高三上学期半期】已知分别是双曲线的左、右焦点,点关于渐近线的对称点恰好落在以为圆心、为半径的圆上,则双曲线的离心率为( )
A. 3 B. C. 2 D.
【答案】C
【解析】由题意,F1(﹣c,0),F2(c,0),一条渐近线方程为,则F2到渐近线的距离为
=b.设F2关于渐近线的对称点为M,F2M与渐近线交于A,∴|MF2|=2b,A为F2M的中点
又0是F1F2的中点,∴OA∥F1M,∴∠F1MF2为直角,
∴△MF1F2为直角三角形,
∴由勾股定理得4c2=c2+4b2
∴3c2=4(c2﹣a2),∴c2=4a2,
∴c=2a,∴e=2.
故选C.
9.【2018届陕西省榆林市第二中学高三上学期期中】已知双曲线C:x2a2-y2b2=1a>0,b>0的左、右焦点分别为F1-c,0,F2c,0,A是双曲线的左顶点,P-a2c,yp在双曲线的一条渐近线上,M为线段F1P的中点,且F1P⊥AM,则该双曲线C的渐近线为( )
A. y=±3x B. y=±2x C. y=±2x D. y=±5x
【答案】A
10.【2017北京,理9】若双曲线的离心率为,则实数m=_________.
【答案】2
【解析】 ,所以 ,解得 .
11.【2017课标1,理】已知双曲线C:(a>0,b>0)的右顶点为A,以A为圆心,b为半径作圆A,圆A与双曲线C的一条渐近线交于M、N两点.若∠MAN=60°,则C的离心率为________.
【答案】
【解析】试题分析:
12.【2017山东,理14】在平面直角坐标系中,双曲线的右支与焦点为的抛物线交于两点,若,则该双曲线的渐近线方程为 .
【答案】
13.【2017届北京市平谷区高三第二学期质量监控】在平面直角坐标系中,若方程表示双曲线,则实数的范围__________;若此双曲线的离心率为,则双曲线的渐近线方程为__________.
【答案】
【解析】(1)若方程表示双曲线,则需满足,解得。
(2)∵双曲线的离心率为, ,
∴
解得,
∴双曲线的方程为,其渐进线方程为。
答案:(1). (2).
14.【2018届江西省临川第二中学高三上期中】设双曲线的左焦点为,左顶点为,过作轴的垂线交双曲线于两点,过作垂直于,过作垂直于,设与的交点为,若到直线的距离大于,则该双曲线的离心率取值范围为__________.
【答案】