- 2021-06-19 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
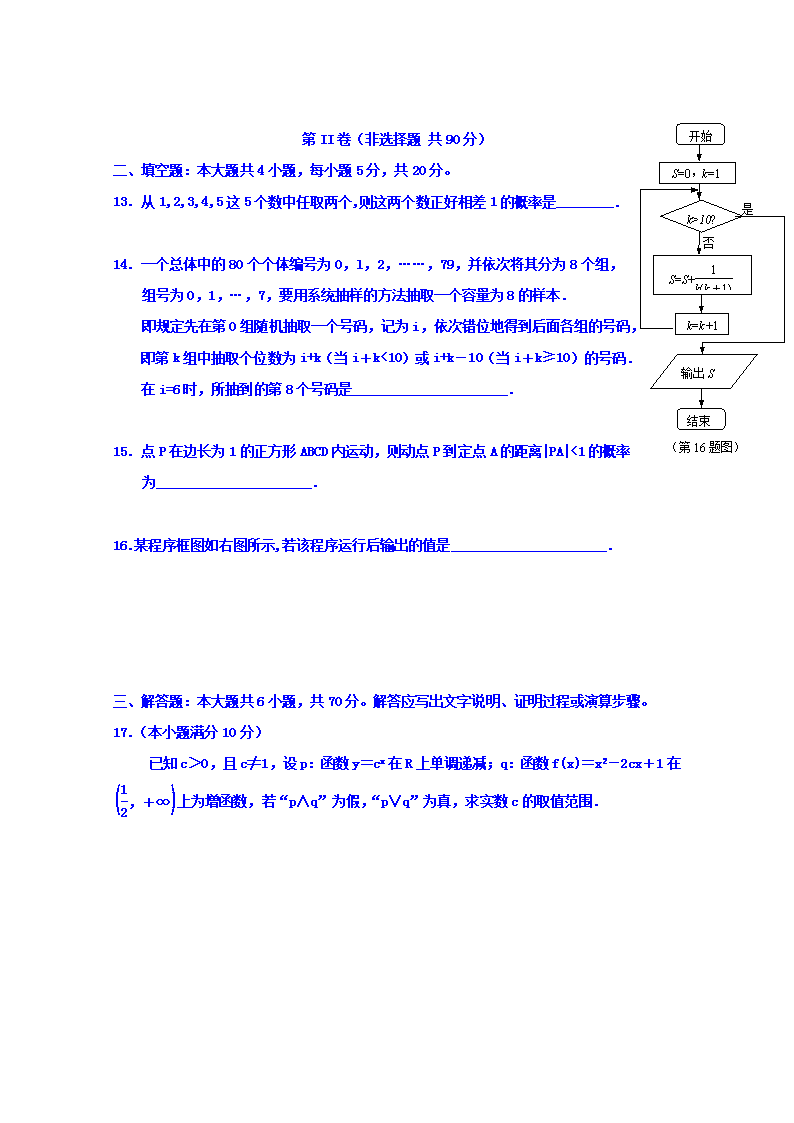
2017-2018学年贵州省铜仁市第一中学高二上学期期中考试数学(文)试题
铜仁一中2017-2018学年高二第一学期半期考试 数学试卷(文) 注意事项: 1.本试卷分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷1至2页,第Ⅱ卷2至4页。满分150分,考试时间120分钟。 2.全部答案在答题卷上完成。 3.考试结束后,将答题卷交回。 第Ⅰ卷(选择题 共60分) 一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。 1.已知命题p:∀x∈R,sin x≤1,则( ). A.¬p:∃x0∈R,sin x0≥1 B.¬p:∀x∈R,sin x≥1 C.¬p:∃x0∈R,sin x0>1 D.¬p:∀x∈R,sin x>1 2.某公司生产三种型号的轿车,产量分别是1600辆、6000辆和2000辆,为检验公司的产品质量,现从这三种型号的轿车种抽取96辆进行检验,这三种型号的轿车依次应抽取() A. 32,32,32 B.16,60,20 C.8,66,22D.24,54,18 3. 下列各数中,最小的数是 ( ) A.75 B. C. D. 4.由右表可计算出变量的线性回归方程为( ) 5 4 3 2 1 2 1.5 1 1 0.5 A.B. C.D. 甲乙 8 0 4 6 3 1 2 5 3 6 8 2 5 4 1 3 8 9 3 1 6 1 7 4 4 5.右图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,中间的数字表示得分的十位数,下列对乙运动员的判断错误的是 ( ) A.乙运动员的最低得分为0分 B.乙运动员得分的众数为31 C.乙运动员的场均得分高于甲运动员 D.乙运动员得分的中位数是28 6. 不等式x2+3x+2>0成立的一个充分不必要条件是( ) A. B. C. D. 7.总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取6个个体,选取方法从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字,则选出来的第6个个体的编号为 ( ) 7816 6572 0802 6314 0702 4369 9728 0198 3204 9234 4934 8200 3623 4869 6938 7481 A.08 B.01 C.02 D.04 8. 用秦九韶算法求多项式时,当时,则=() A.4 B.9 C.15 D.29 9. 从装有2个红球和2个白球的红袋内任取两个球,那么下列事件中,互斥事件的个数是( ) ①至少有1个白球;都是白球. ②至少有1个白球;至少有1个红球. ③恰好有1个白球;恰好有2个白球. ④至少有1个白球;都是红球. A.0 B.1 C.2 D.3 10.右图给出的是计算的值的一个流程图,其中判断框内应填入的条件是( ) A. B. C. D. 11.已知某8个数据的平均数为8,方差为4,现又加入一个新数据8,此时 这9个数的平均数为,方差为s2,则( ) A. =8,s2<4 B.=8,s2>4 C.>8,s2<4 D.>8,s2>4 12.圆O内有一内接正三角形,向圆O内随机投一点,则该点落在正三角形 内的概率为( ) A. B. C. D. 开始 S=0,k=1 k>10? S=S+ k=k+1 输出S 结束 是 否 (第16题图) 第II卷(非选择题 共90分) 二、填空题:本大题共4小题,每小题5分,共20分。 13. 从1,2,3,4,5这5个数中任取两个,则这两个数正好相差1的概率是________. 14. 一个总体中的80个个体编号为0,l,2,……,79,并依次将其分为8个组, 组号为0,1,…,7,要用系统抽样的方法抽取一个容量为8的样本. 即规定先在第0组随机抽取一个号码,记为i,依次错位地得到后面各组的号码, 即第k组中抽取个位数为i+k(当i+k<10)或i+k-10(当i+k≥10)的号码. 在i=6时,所抽到的第8个号码是______________________. 15. 点P在边长为1的正方形ABCD内运动,则动点P到定点A的距离|PA|<1的概率 为______________________. 16.某程序框图如右图所示,若该程序运行后输出的值是______________________. 三、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。 17.(本小题满分10分) 已知c>0,且c≠1,设p:函数y=cx在R上单调递减;q:函数f(x)=x2-2cx+1在上为增函数,若“p∧q”为假,“p∨q”为真,求实数c的取值范围. 18.(本小题满分12分) 袋中有大小相同的红、白两种颜色的球各1个,从中任取1只,有放回地抽取3次.求: (1)3只颜色不全相同的概率; (2) 三次抽取的球中红色球出现的次数多于白色球出现的次数。 19.(本小题满分12分) 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产耗能y(吨标准煤)的几组对应数据。 X 3 4 5 6 y 2.5 3 4 4.5 (1)请根据上表提供的数据,用最小二乘法 求出y关于x的线性回归方程 (2)已知技改前100吨甲产品的生产能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (回归直线方程是:,其中,) 20.(本小题满分12分) 某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题: 组号 分组 频数 频率 第1组 [50,60) 5 0.05 第2组 [60,70) a 0.35 第3组 [70,80) 30 b 第4组 [80,90) 20 0.20 第5组 [90,100] 10 0.10 合计 100 1.00 (1) 求a,b的值; (2) 若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率. 21.(本小题满分12分) 将一枚骰子抛掷两次,若先后出现的点数分别为m、n (1)求方程x2+mx+n=0有实根的概率; (2)若点P的坐标为(m,n),求点P落在圆x2+y2=16内的概率. 22.在墙上挂着一块边长为16cm 的正方形木板,上面画了小、中、大三个同心圆,半径分别为2cm,4cm,6cm,某人站在3m处向此板投镖.设投镖击中线上或没有投中木板时都不算,可重投,问: (1)投中大圆内的概率是多少? (2)投中小圆与中圆形成的圆环的概率是多少? (3)投中大圆之外的概率是多少? 铜仁一中2017-2018学年高二(上)期中考试 数学试卷(文)答案 一、 选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C B C D A A D C C D A B 二、填空题 (13)(14)73(15) (16) 三、解答题 17、∵函数y=cx在R上单调递减, ∴0<c<1.(2分) 即p:0<c<1.∵c>0且c≠1,∴¬p:c>1. 又∵f(x)=x2-2cx+1在上为增函数, ∴c≤.即q:0<c≤. ∵c>0且c≠1,∴¬q:c>且c≠1. 又∵“p∨q”为真,“p∧q”为假,∴p真q假或p假q真. ①当p真,q假时,{c|0<c<1}∩=; ②当p假,q真时,{c|c>1}∩=∅. 综上所述,实数c的取值范围是. 18、基本事件:(红红红)(红红白)(红白红)(白红红)(红白白)(白红白)(白白红)(白白白) (1) (2) 19、(1)对照数据,计算得: 已知 所以,由最小二乘法确定的回归方程的系数为: 因此,所求的线性回归方程为 (2)由(1)的回归方程及技改前生产100吨甲产品的生产能耗,得降低的生产能耗约为 20、(1)a=100-5-30-20-10=35,b=1-0.05-0.35-0.20-0.10=0.30 (2)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组分别为,第3组:×30=3人,第4组:×20=2人,第5组:×10=1人,所以第3、4、5组应分别抽取3人、2人、1人. 设第3组的3位同学为A1、A2、A3,第4组的2位同学为B1、B2,第5组的1位同学为C1,则从6位同学中抽2位同学有15种可能,如下: (A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1).其中第4组被入选的有9种, 所以其中第4组的2位同学至少有1位同学入选的概率为=. 21、我们用列表的方法列出所有可能结果: 掷 第 二 颗 得 到 的 点 数 掷 第 一 颗 得 到 的 点 数 1 2 3 4 5 6 1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6) 2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6) 3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6) 4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) 5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6) 6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6) 由表中可知,抛掷两颗骰子,总的事件有36个。 (1) 记“方程x2+mx+n=0有实根的概率”为事件A,事件的基本事件有19个,P(A)=. (2) 记“P(m,n)落在圆x2+y2=16内的概率”为事件B, 事件的基本事件有8个, P(B)=. 22、解:此题为几何概型中的面积比问题 (1)设{投中大圆}为事件A,则 (2)设{投中小圆与中圆形成的圆环}为事件B,则 (3)设{投中大圆之外}为事件C,则事件A与事件C互为对立事件,故查看更多