- 2021-06-19 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020高中数学 章末综合测评3 统计案例 新人教A版选修2-3
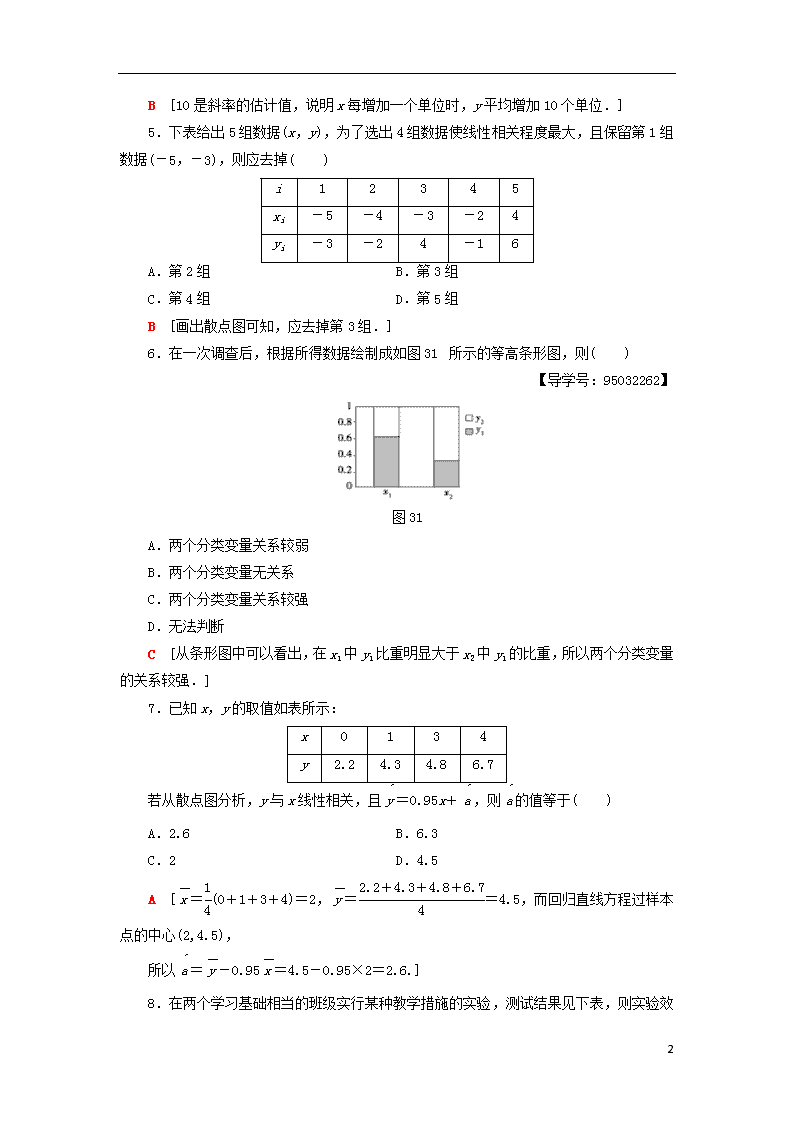
章末综合测评(三) 统计案例 (时间120分钟,满分150分) 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.下面是一个2×2列联表 y1 y2 总计 x1 a 21 73 x2 2 25 27 总计 b 46 100 其中a,b处填的值分别为( ) A.52,54 B.54,52 C.94,146 D.146,94 A [由a+21=73,得a=52,a+2=b,得b=54.] 2.在2×2列联表中,下列哪两个比值相差越大,两个分类变量有关系的可能性就越大( ) 【导学号:95032261】 A.与 B.与 C.与 D.与 A [当ad与bc相差越大,两个分类变量有关系的可能性越大,此时与相差越大.] 3.已知变量x与y正相关,且由观测数据算得样本平均数=3,=3.5,则由该观测数据算得的线性回归方程可能是( ) A.=0.4x+2.3 B.=2x-2.4 C.=-2x+9.5 D.=-0.3x+4.4 A [因为变量x和y正相关,则回归直线的斜率为正,故可以排除选项C和D.因为样本点的中心在回归直线上,把点(3,3.5)的坐标分别代入选项A和B中的直线方程进行检验,可以排除B,故选A.] 4.设有一个线性回归方程为=-2+10x,则变量x增加一个单位时( ) A.y平均减少2个单位 B.y平均增加10个单位 C.y平均增加8个单位 D.y平均减少10个单位 9 B [10是斜率的估计值,说明x每增加一个单位时,y平均增加10个单位.] 5.下表给出5组数据(x,y),为了选出4组数据使线性相关程度最大,且保留第1组数据(-5,-3),则应去掉( ) i 1 2 3 4 5 xi -5 -4 -3 -2 4 yi -3 -2 4 -1 6 A.第2组 B.第3组 C.第4组 D.第5组 B [画出散点图可知,应去掉第3组.] 6.在一次调查后,根据所得数据绘制成如图31所示的等高条形图,则( ) 【导学号:95032262】 图31 A.两个分类变量关系较弱 B.两个分类变量无关系 C.两个分类变量关系较强 D.无法判断 C [从条形图中可以看出,在x1中y1比重明显大于x2中y1的比重,所以两个分类变量的关系较强.] 7.已知x,y的取值如表所示: x 0 1 3 4 y 2.2 4.3 4.8 6.7 若从散点图分析,y与x线性相关,且=0.95x+,则的值等于( ) A.2.6 B.6.3 C.2 D.4.5 A [=(0+1+3+4)=2,==4.5,而回归直线方程过样本点的中心(2,4.5), 所以=-0.95=4.5-0.95×2=2.6.] 9 8.在两个学习基础相当的班级实行某种教学措施的实验,测试结果见下表,则实验效果与教学措施( ) 优、良、中 差 总计 实验班 48 2 50 对比班 38 12 50 总计 86 14 100 A.有关 B.无关 C.关系不明确 D.以上都不正确 A [随机变量K2的观测值k=≈8.306>6.635,则有99%的把握认为“实验效果与教学措施有关”.] 9.某地财政收入x与支出y满足线性回归方程=x++e(单位:亿元),其中=0.8,=2,|e|<0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( ) 【导学号:95032263】 A.10亿 B.9亿 C.10.5亿 D.9.5亿 C [代入数据得y=10+e,∵|e|<0.5, ∴|y|<10.5,故不会超过10.5亿.] 10.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表: 收入x(万元) 8.2 8.6 10.0 11.3 11.9 支出y(万元) 6.2 7.5 8.0 8.5 9.8 根据上表可得回归直线方程=x+,其中=0.76,=-.据此估计,该社区一户年收入为15万元家庭的年支出为( ) A.11.4万元 B.11.8万元 C.12.0万元 D.12.2万元 B [由题意知,==10, ==8, ∴=8-0.76×10=0.4, ∴当x=15时,=0.76×15+0.4=11.8(万元).] 11.设两个变量x和y之间具有线性相关关系,它们的相关系数是r,y关于x 9 的回归直线的斜率是b,纵轴上的截距是a,那么必有( ) A.b与r的符号相同 B.a与r的符号相同 C.b与r的符号相反 D.a与r的符号相反 A [因为b>0时,两变量正相关,此时r>0;b<0时,两变量负相关,此时r<0.] 12.两个分类变量X和Y,值域分别为{x1,x2}和{y1,y2},其样本频数分别是a=10,b=21,c+d=35.若X与Y有关系的可信程度不小于97.5%,则c等于( ) A.3 B.4 C.5 D.6 附: P(K2≥k0) 0.05 0.025 k0 3.841 5.024 A [2×2列联表如下: x1 x2 总计 y1 10 21 31 y2 c d 35 总计 10+c 56-c 66 故K2的观测值k=≥5.024. 把选项A,B,C,D代入验证可知选A.] 二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中的横线上) 13.某大型企业人力资源部为了研究企业员工工作积极性和对企业改革态度的关系,随机抽取了189名员工进行调查,所得数据如下表所示: 积极支持企业改革 不赞成企业改革 总计 工作积极 54 40 94 工作一般 32 63 95 总计 86 103 189 对于人力资源部的研究项目,根据上述数据试求K2的观测值为_______. 【导学号:95032264】 10.76 [根据列联表中的数据,得到k=≈10.76.] 14.已知样本容量为11,计算得i=510,i=214,回归方程为=0.3x+,则≈________,≈________.(精确到0.01) 9 46.36 5.55 [由题意得=i=≈46.36,=i=,因为=0.3+,所以=0.3×+,可得≈5.55.] 15.某部门通过随机调查89名工作人员的休闲方式是读书还是健身,得到的数据如下表: 读书 健身 总计 女 24 31 55 男 8 26 34 总计 32 57 89 在犯错误的概率不超过________的前提下性别与休闲方式有关系. 0.10 [由列联表中的数据,得K2的观测值为k=≈3.689>2.706, 因此,在犯错误的概率不超过0.10的前提下认为性别与休闲方式有关系.] 16.某地区恩格尔系数Y(%)与年份x的统计数据如下表: 年份x 2006 2007 2008 2009 恩格尔系数Y(%) 47 45.5 43.5 41 从表中可以看出Y与x线性相关,且可得回归方程为=x+4 055.25,据此模型可预测2019年该地区的恩格尔系数Y(%)为________. 【导学号:95032265】 17.25 [由表可知=2 007.5,=44.25. 因为= +4 055.25, 即44.25=2 007.5+4 055.25, 所以≈-2,所以回归方程为=-2x+4 055.25,令x=2 019,得=17.25.] 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)x与y有如下五组数据, x 1 2 3 5 10 y 10 5 4 2 2 试分析x与y之间是否具有线性相关关系.若有,求出回归直线方程;若没有,说明理由. [解] 作出散点图,如图所示: 9 由散点图可以看出,x与y不具有线性相关关系. 18.(本小题满分12分)某运动队研制了一种有助于运动员在大运动量的训练后快速恢复体力的口服制剂,为了实验新药的效果而抽取若干名运动员来实验,所得资料如下: 试区分该种药剂对男、女运动员产生的效果的强弱. [解] 对男运动员K2=≈7.013>6.635, 所以有99%的把握认为药剂对男运动员有效. 对女运动员K2=≈0.076≤2.706, 所以没有充足的证据显示药剂与女运动员体力恢复有关系. 因此该药对男运动员药效较好. 19.(本小题满分12分)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了4次试验,得到数据如下: 零件的个数x(个) 2 3 4 5 加工的时间y(小时) 2.5 3 4 4.5 (1)在给定坐标系(如图32)中画出表中数据的散点图: 图32 (2)求y关于x的线性回归方程=x+; (3)试预测加工10个零件需要的时间. 【导学号:95032266】 9 [解] (1)散点图如图所示: (2)由表中数据得=3.5,=3.5, (xi-)(yi-)=3.5,(xi-)2=5, 由公式计算得=0.7,=-=1.05,所以所求线性回归方程为=0.7x+1.05. (3)当x=10时,=0.7×10+1.05=8.05, 所以预测加工10个零件需要8.05小时. 20.(本小题满分12分)有两个分类变量x与y,其一组观测值如下面的2×2列联表所示: y1 y2 x1 a 20-a x2 15-a 30+a 其中a,15-a均为大于5的整数,则a取何值时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系? [解] 查表可知,要使在犯错误的概率不超过0.1的前提下认为x与y之间有关系,则k≥2.706,而 k= ==. 由k≥2.706,得a≥7.19或a≤2.04. 又a>5且15-a>5,a∈Z,解得a=8或9, 故a为8或9时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系. 21.(本小题满分12分)为了搞好某运动会的接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动. (1)根据以上数据完成以下2×2列联表: 喜爱运动 不喜爱运动 总计 9 男 10 16 女 6 14 总计 30 (2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关? (3)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少? 【导学号:95032267】 [解] (1)2×2列联表如下: 喜爱运动 不喜爱运动 总计 男 10 6 16 女 6 8 14 总计 16 14 30 (2)假设:是否喜爱运动与性别无关,由已知数据可求得 k2=≈1.157 5<2.706. 因此,在犯错误的概率不超过0.10的前提下不能判断喜爱运动与性别有关. (3)喜欢运动的女志愿者有6人,从中抽取2人,有C=15种取法. 其中两人都不会外语的只有一种取法. 故抽出的志愿者中至少有1人能胜任翻译工作的概率是P=1-=. 22.(本小题满分12分)某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表: 年 份 2007 2008 2009 2010 2011 2012 2013 年份代号t 1 2 3 4 5 6 7 人均纯收入y 2.9 3.3 3.6 4.4 4.8 5.2 5.9 (1)求y关于t的线性回归方程; (2)利用(1)中的回归方程,分析2007年至2013年该地 区农村居民家庭人均纯收入的变化情况,并预测该地区2018年农村居民家庭人均纯收入. 附:回归直线的斜率和截距的最小二乘法估计公式分别为: =,=-. 9 [解] (1)由所给数据计算得=(1+2+3+4+5+6+7)=4, =(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3, (ti-)2=9+4+1+0+1+4+9=28, (ti-)(yi-)=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14, ===0.5, =-=4.3-0.5×4=2.3, 所求回归方程为=0.5t+2.3. (2)由(1)知,b=0.5>0,故2007年至2013年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元. 将2018年的年份代号t=12代入(1)中的回归方程,得 =0.5×12+2.3=8.3, 故预测该地区2018年农村居民家庭人均纯收入为8.3千元. 9查看更多