数学理卷·2017届辽宁省沈阳铁路实验中学高三第二次月考（2016

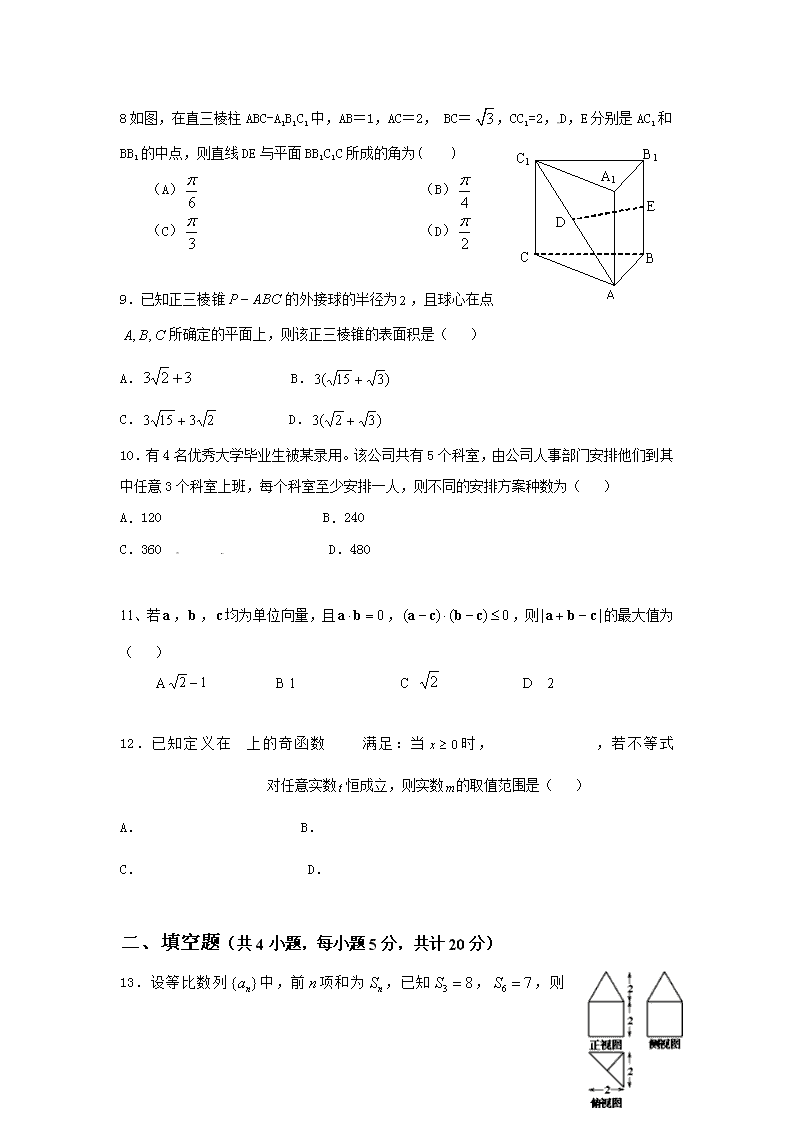
数学理卷·2017届辽宁省沈阳铁路实验中学高三第二次月考（2016

沈阳铁路实验中学2016~2017学年度上学期第二次月考 高三数学（理）‎ 命题人：殷裕民 审题人：佟胤琳 时间：120分钟 ‎ 一、选择题（共12小题，每小题5分，共计60分）‎ ‎1．已知集合，，则（ ）‎ A． B．‎ C． D．‎ ‎2．若（为虚数单位），则的虚部是（ ）‎ A．1 B．‎-1 C． D．‎ ‎3．下列函数中是偶函数且值域为的函数是（ ）‎ A． B． ‎ C． D．‎ ‎4．已知为互不重合的三个平面，命题 若，，则∥；命题 若上不共线的三点到的距离相等，则∥.对以上两个命题，下列结论中正确的是（ ）‎ ‎（A）命题“ ”为真 （B）命题“ ”为假 ‎（C）命题“ ”为假 （D）命题“ ”为真 ‎5．若，则的值为（ ）‎ A． B． C． D．‎ ‎6．若，则的展开式中常数项为（ ）‎ A． B． C． D．‎ ‎7．已知平面向量的夹角为，且，，在中，，，为边的中点，则（ ）‎ A．2 B．‎4 C．6 D．8‎ ‎8如图，在直三棱柱ABC-A1B‎1C1中，AB＝1，AC＝2， BC＝，CC1=2，D，E分别是AC1和BB1的中点，则直线DE与平面BB‎1C1C所成的角为( )‎ ‎ （A） （B） ‎ ‎ （C） （D）‎ ‎9．已知正三棱锥的外接球的半径为，且球心在点所确定的平面上，则该正三棱锥的表面积是（ ）‎ A． B．‎ C． D．‎ ‎10．有4名优秀大学毕业生被某录用。该公司共有5个科室，由公司人事部门安排他们到其中任意3个科室上班，每个科室至少安排一人，则不同的安排方案种数为（ ）‎ A．120 B．240 ‎ C．360 D．480‎ ‎11、若，，均为单位向量，且，，则的最大值为（ ）‎ A B ‎1 ‎ C D 2‎ ‎12．已知定义在上的奇函数满足：当时，，若不等式对任意实数恒成立，则实数的取值范围是（ ）‎ A． B．‎ C． D．‎ 二、填空题（共4小题，每小题5分，共计20分）‎ ‎13．设等比数列中，前项和为，已知，，则 ‎_________．‎ ‎14．某几何体的三视图如图所示（单位：），则该几何体的体积是_____．‎ ‎15．如图是判断“实验数”的流程图，在[30，80]内的所有整数中，“实验数”的个数是________．‎ ‎16．函数的定义域为实数集，对于任意的，，若在区间上函数恰有三个不同的零点，则实数的取值范围是 ．‎ 三、解答题（共6题， 17~21每题12分，选修10分，总计70分）‎ ‎17.已知是等差数列，是等比数列，为数列的前项和，，且，（）．‎ ‎（1）求和；（2）若，求数列的前项和．‎ ‎18．在△ABC中，所对的边分别为,．‎ ‎（1）求角C的大小；（2）若b＝4，△ABC的面积为6，求边c的值．‎ ‎19下图是一几何体的直观图、主视图、俯视图、左视图．‎ ‎ （Ⅰ）若为的中点，求证：面;‎ ‎ （Ⅱ）证明面;‎ ‎（Ⅲ）求二面角E—PC—D的余弦值．‎ ‎20．众所周知，乒乓球是中国的国球，乒乓球队内部也有着很严格的竞争机制，为了参加国际大赛，种子选手甲与三位非种子选手乙、丙、丁分别进行一场内部对抗赛，按以往多次比赛的统计，甲获胜的概率分别为，，，且各场比赛互不影响．‎ ‎（1）若甲至少获胜两场的概率大于，则甲入选参加国际大赛参赛名单，否则不予入选，问甲是否会入选最终的大名单？‎ ‎（2）求甲获胜场次的分布列和数学期望．‎ ‎21．已知函数．‎ ‎（1）若在处取得极小值，求的值；‎ ‎（2）若在上恒成立，求的取值范围；‎ ‎（3）求证：当时，．‎ 请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题记分.做答时请写清题号.‎ ‎22．选修4-4：坐标系与参数方程 在极坐标系中，已知射线，动圆．‎ ‎（1）求，的直角坐标方程；‎ ‎（2）若射线与动圆相交于与两个不同点，求的取值范围．‎ ‎23．选修4—5：不等式选讲 已知函数.‎ ‎（Ⅰ）若，使得不等式成立，求的取值范围；‎ ‎（Ⅱ）求使得等式成立的的取值范围.‎ 上学期第二次月考试题答案 ‎1.D 2.B 3.D 4.C 5.A 6.C 7.A 8.A 9.B 10.C 11.C 12.A ‎13. 14. 15. 16.‎ ‎17试题解析：（1）设的公差为，的公比为， ‎ 由题意得解得或 ‎∴，或，．‎ ‎（2）若，由（1）知，‎ ‎∴，‎ ‎∴．‎ ‎18试题解析：（1）．⇒，‎ ‎⇒，⇒，‎ ‎⇒，⇒，⇒，⇒，，（2）∵，，∴，∵,∴．‎ ‎20．（1）甲会入选最终的大名单；（2）分布列见解析，．‎ ‎【解析】‎ 试题分析：（1）借助题设条件运用概率的知识推证；（2）借助题设运用随机变量的概率分布和数学期望公式求解．‎ 试题解析：‎ ‎（1）记与进行对抗赛获胜的事件分别为，至少获胜两场的事件为，‎ 则，，．‎ 由于事件相互独立，‎ 所以 ‎，‎ 由于，所以会入选最终的大名单．………………6分 ‎（2）获胜场数的可能取值为0,1,2,3，则 ‎，………………7分 ‎，‎ ‎．‎ 所以获胜场数的分布列为：‎ ‎………………………………11分 数学期望为．………………12分 ‎21．（1）；（2）；（3）证明见解析.‎ ‎【解析】‎ 试题分析：（1）求函数的导数，根据求出的值，但需要验证；（2）需要分类讨论，根据导数求出函数的最小值；（3）由（2）可得，利用裂项求和证明即可.‎ 试题解析：（1）∵的定义域为，，‎ ‎∵在处取得极小值，∴，即，此时，经验证是的极小值点，故．‎ ‎（2）∵，‎ ‎①当时，，∴在上单调递减，∴当时，矛盾．‎ ‎②当时，，令，得；，得．‎ ‎（i）当，即时，时，，即递减，∴矛盾．‎ ‎（ii）当，即时，时，，即递增，∴满足题意．‎ 综上:．‎ ‎（3）证明：由（2）知令，当时，（当且仅当时取“”）‎ ‎∴当时，．‎ 即当，有 ‎．‎ ‎22．（1），；（2）．‎ ‎【解析】‎ 试题分析：（1）借助题设条件运用极坐标与直角坐标之间的关系求解；（2）借助题设运用二次方程的有关知识建立不等式组探求．‎ 试题解析：‎ ‎（1）∵，，∴．‎ ‎∴的直角坐标方程为．………………2分 ‎∵，∴的直角坐标方程为．………………4分 ‎（2）联立，‎ 关于的一元二次方程在内有两个实根．‎ 即，‎ 得，‎ 解得．‎ ‎23．解：（Ⅰ）由= -----------3分 使得不等式成立的的取值范围是 -----------5分 ‎（Ⅱ）由= -----------7分 所以，当且仅当时取等--------9分 所以的取值范围是 -----------10分