- 2021-06-19 发布 |
- 37.5 KB |
- 9页

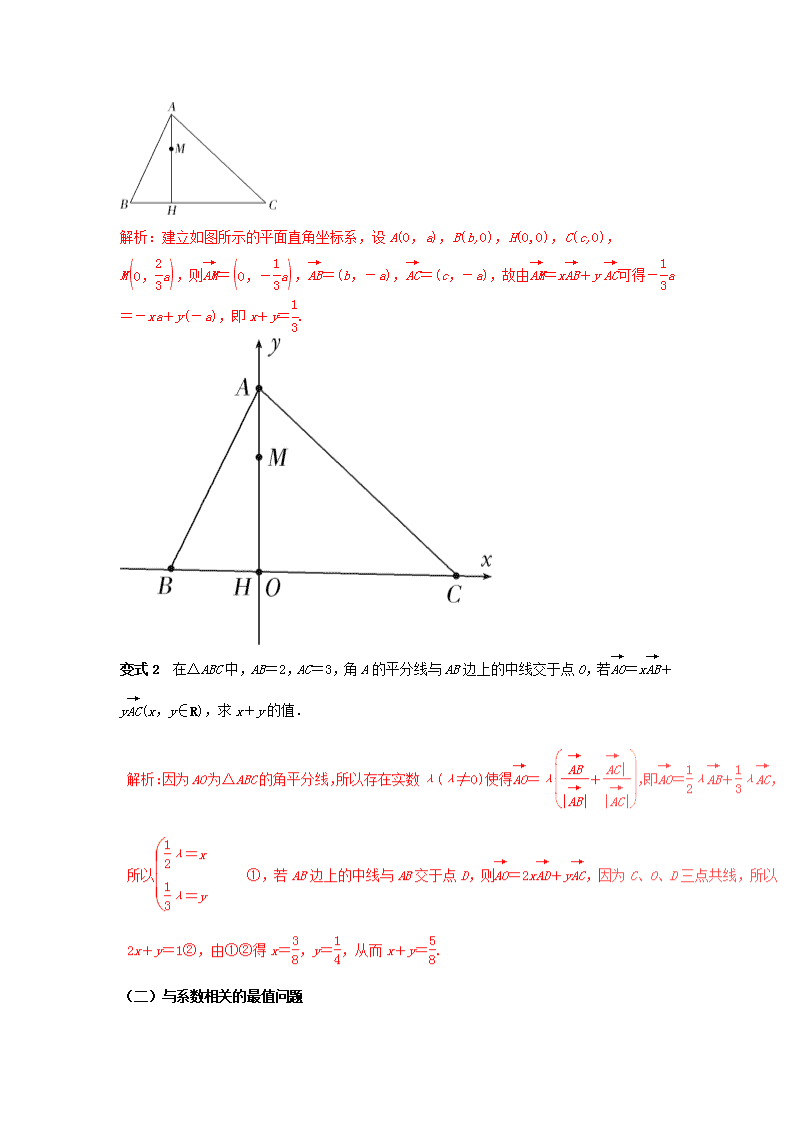
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习平面向量的线性表示学案(江苏专用)
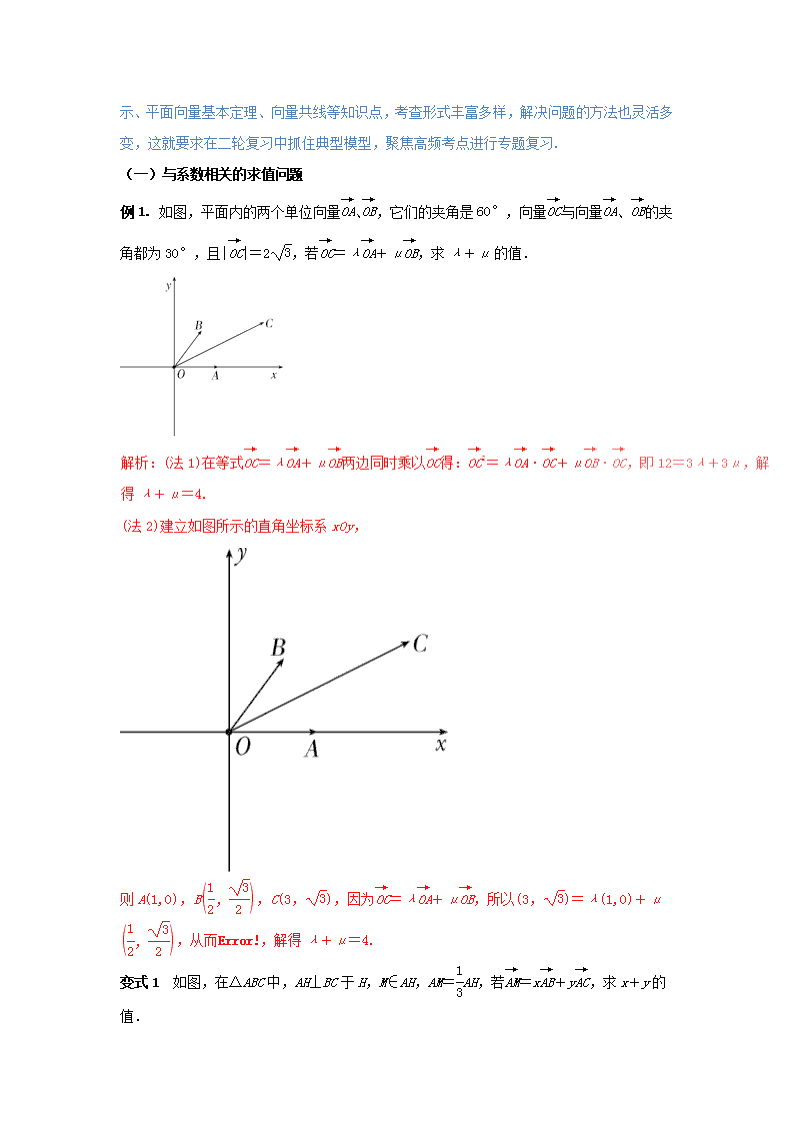
【热身训练】 1.若e1,e2是平面内所有向量的一组基底,那么下列结论正确的是________. (1) 若实数λ1,λ2使得λ1e1+λ2e2=,则λ1=λ2=0; (2) 空间任意一个向量a都可以表示为a=λ1e1+λ2e2(λ1,λ2∈R); (3)对于这一平面内的任意向量,使a=λ1e1+λ2e2成立的实数对λ1,λ2有无数对. 2.在△ABC中,若点D,E,F依次是边AB上的四等分点,设=e1,=e2,用e1,e2表示,则=________. 解析:在△ABC中,=+=e1-e2,=,所以=+=e2+(e1-e2)=e1+e2. 3.设点A,B, C是直线l上不同的三点,点O是直线l外一点,若=λ+μ,则λ+μ的值为________. 解析:因为点A,B,C三点共线,所以=x,又因为=+=+x=+x(-)=(1-x)+x,所以λ+μ=1. 4.在△ABC中,D,E分别是边BC上的两个三等分点,点P是线段DE上一点,且=x+y(x,y∈R),则xy的取值范围为________. 解析:因为点P,B,C三点共线,所以x+y=1,且≤x≤,xy=x(1-x)=-+,所以xy∈. 【热点追踪】 从这几年的江苏卷 看,平面向量的线性表示考查频繁,如2015年第6题,2017年第12题,主要考查 生对平面向量线性运算的掌握情况,多以中档题呈现.涉及到平面向量的线性表示、平面向量基本定理、向量共线等知识点,考查形式丰富多样,解决问题的方法也灵活多变,这就要求在二轮复习中抓住典型模型,聚焦高频考点进行专题复习. (一)与系数相关的求值问题 例1. 如图,平面内的两个单位向量、,它们的夹角是60°,向量与向量、的夹角都为30°,且||=2,若=λ+μ,求λ+μ的值. 则A(1,0),B,C(3,),因为=λ+μ,所以(3,)=λ(1,0)+μ,从而,解得λ+μ=4. 变式1 如图,在△ABC中,AH⊥BC于H,M∈AH,AM=AH,若=x+y,求x+y的值. 解析:建立如图所示的平面直角坐标系,设A(0,a),B(b,0),H(0,0),C(c,0),M,则=,=(b,-a),=(c,-a),故由=x+y可得-a=-xa+y(-a),即x+y=. 变式2 在△ABC中,AB=2,AC=3,角A的平分线与AB边上的中线交于点O,若=x+y(x,y∈R),求x+y的值. (二)与系数相关的最值问题 例2. 如图,在扇形OAB中,∠AOB=60°,C为弧AB上的一个动点,若=x+y(x,y∈R),求x+4y的取值范围. 解析:建立如图所示的直角坐标系,设此扇形的半径为1,∠AOB=60°,所以A,B(1,0), 变式1 设点A,B,C为单位圆上不同的三点,若∠ABC=,=m+n(m,n∈R),则m+n的最小值为________. 解析:因为∠ABC=,所以∠AOC=,不妨设A(1,0),C(0,1),B(cos θ,sin θ),θ∈,则cos θ=m,sin θ=n⇒m+n=cos θ+sin θ=sin≥-,当且仅当θ=时取等号. 变式2 如图,在正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧上的任意一点,设向量= λ+μ(λ,μ∈R),求λ+μ的最小值. 解析:以A为原点,以AB所在直线为x轴,建立平面直角坐标系, 设正方形ABCD的边长为1,则E,C(1,1),D(0,1),A(0,0),设P(cos θ,sin θ),所以=(1,1),又=λ+μ.故λ(,-1)+μ(cos θ,sin θ)=(1,1), (三)向量共线定理的应用 例3. 如图,在△ABC中,点O是BC的中点,过O的直线分别交直线AB,AC于不同的两点M,N,若=m,=n,求m+n的值. 解析:=+=+=+(-)=+,将=m,=n代入可得:=+,设=λ(0<λ<1),可得=+=+λ=+λ(-)=(1-λ)+λ,由平面向量基本定理可得,故=1,所以m+n的值为2. 变式1 如图,经过△ABO的重心G的直线与OA,OB交于点P,Q,设=m,=n,m,n∈R,则+的值为________. ⇒+=1⇒+=3,故+的值为3. 变式2 已知点O是△ABC的外心,AB=AC=2,若=x+y(xy≠0),且x+2y=1,则△ABC的面积等于________. 【乘热打铁】 1.设D为△ABC所在平面内一点,=3,=m+n,则n-m=________. 解析:因为=3,=+=+=+(+)=-+,所以m=-,n=,故n-m=. 2. 在△ABC中,AB=2,BC=3,∠ABC=60°,AD为BC边上的高,O为AD的中点,若=λ+μ,则λ+μ=________. 解析:在Rt△ABD中,BD=ABcos 60°=1,所以=,所以=,因为=+=+,所以2=+,即=+,所以λ=,μ=,即λ+μ=. 3. 如图所示,己知点G是△ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且AM=x,=y ,则的值为________. 解析:设=m+n,因为M、G、N三点共线, 则m+n=1,因为点G是△ABC的重心,则有=(+), 又=mx+ny,根据平面向量基本定理得mx=ny=, 即x=,y=,代入得=. 4. 在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=AB=4,CD=1,动点P在边BC上,且满足=m+n(m,n>0),求+的最小值.[ : ]查看更多